多维随机变量及其分布
(一) 二维随机变量
1 概念
2 联合分布函数(如果说之前一维积分是面积,那这里二维积分就是体积)
2.1 概念:F(x, y) = P{X \(\leq\) x, Y \(\leq\) y}
2.2 性质
(1) 单调性(固定一个,看另一个)
(2) 右连续性(固定一个,看另一个)
(3) 有界性(全体积为1)
(4) 非负性(下面这个公式重点根据旁边的图理解是如何计算的)

3 边缘分布函数(求哪一个,保留哪一个,另一个极限取到无穷)
\(F_X(x) = F(x, +\infty)\)
\(F_Y(y) = F(+\infty, y)\)
(二) 二维离散型随机变量
1 联合分布律
2 边缘分布律
3 条件分布律
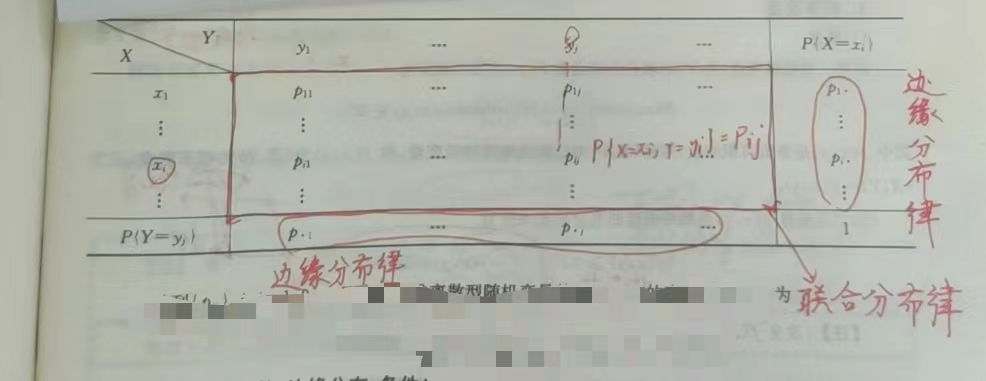
4 独立性:\(\forall\ i, j, P_{ij} = P_i.P_j. \Longleftrightarrow X, Y相互对立\)
(三) 二维连续型随机变量
1 概率密度
1.1 联合概率密度:f(x, y)
1.2 边缘概率密度:求谁不积谁,不积先定限,限内画条线,先交取下限,后交取上限
\(f_X(x) = \int_{-\infty}^{+\infty}f(x, y)\,dy\)(表示的几何意义是求沿X = x对几何体切一刀得到的切片面积,关键是要求y的积分范围,方法是求谁不积谁,限内画条线,先交取下限,后交取上限)
\(f_Y(y) = \int_{-\infty}^{+\infty}f(x, y)\,dx\)
2 分布函数
2.1 联合分布函数:F(x, y) = P{X \(\leq\) x, Y \(\leq\) y} = \(\int_{-\infty}^{y} \int_{\infty}^{x}f(u, v)\, dudv\)
2.2 边缘分布函数
已知联合概率密度\(f(x, y)\)
\(F_X(x) = \int_{-\infty}^xf_X(t)\, dt = \int_{-\infty}^{x}[\int_{-\infty}^{+\infty}f(u, v)du]dv\)
\(F_Y(y) = \int_{-\infty}^yf_Y(t)\, dt = \int_{-\infty}^{y}[\int_{-\infty}^{+\infty}f(u, v)dv]du\)
已知联合分布函数\(F(x, y)\)(不用积分了!取极限到无穷就行)
\(F_X(x) = F(x, +\infty)\)
\(F_Y(y) = F(+\infty, y)\)
2.3 与概率密度关系
2.3.1 联合 :联合分布函数F(x, y)求两次偏导就可以得到联合概率密度f(x, y), f(x, y)求二重积分就可以得到F(x, y)
2.3.2 边缘:\(边沿分布函数F_X(x)和边缘概率密度f_X(x)不存在这种关系,Y同理\)
举个例子

3 条件:\(条件 = \frac{联合}{边缘}\)
3.1 条件概率密度
\(f_{Y|X}(y|x) = \frac{f(x, y)}{f_{X}(x)}\)
\(f_{X|Y}(x|y) = \frac{f(x, y)}{f_{Y}(y)}\)
3.2 条件分布函数:哪个是条件,哪个保留,积另外一个,以\(F_{Y|X}(y|x)\)为例,因为叫在X = x条件下的条件分布函数,所以是对y积分
\(F_{Y|X}(y|x) = \int_{-\infty}^{y}f_{Y|X}(y|x)dy\)
\(F_{X|Y}(x|y) = \int_{-\infty}^{x}f_{X|Y}(x|y)dx\)
举个例子
4 独立性:
4.1 从概率密度角度:\(f(x, y) = f_{X}(x)f_{Y}(y)\)
4.2 从分布函数角度:\(F(X, Y) = F_X(x)F_Y(y)\)
举个例子,也涉及概率密度与分布函数关系

4.3 相互独立随机变量函数的分布及卷积公式:积谁不换谁,换完求偏导加绝对值,如果独立,进一步拆分
设(X, Y)~f(x, y)
(1) 和的分布:Z = X + Y的概率密度\(f_Z(z) = \int_{-\infty}^{+\infty}f(x, z-x)dx\)(换成y同理),进一步如果X与Y相互独立,\(f_Z(z) = \int_{-\infty}^{+\infty}f(x, z-x)dx = \int_{-\infty}^{+\infty}f_X(x)f_Y(z-x)dx\)
(2) 差的分布
(3) 积的分布
(4) 商的分布
(5) max{X, Y}的分布
(6) min{X, Y}的分布
5 两个常见的二维连续分布
5.1 二维均匀分布
5.2 二维正态分布(这个有大问题)
概念

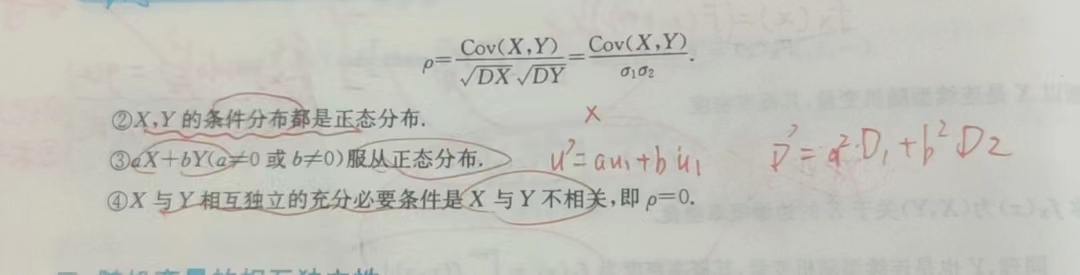
题型


(四) 经典题型:
1 求二维随机变量在限制条件下概率
1.1 二维随机变量相互独立,常见于两个相互独立的正态分布,直接将限制条件转换成一个新函数

1.2 二维随机变量独立性未知,只知f(x, y)
1.2.1 找出正概率区间
1.2.2 画出正概率区间与限定区间的交集
1.2.3 计算二重积分或求和
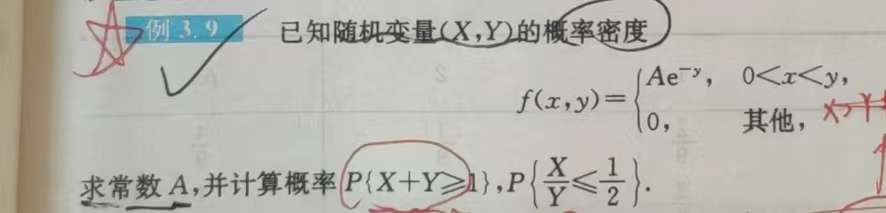
2 二维复合成一维(Z = F(X, Y)),求复合后的概率密度
2.1连续-连续

法一:
1 求联合概率密度
2 通过代入定义\(F_Z(z) = P\left\{Z \leq z\right\} = P\left\{F(X, Y) \leq z\right\}\)转换成前面求限制条件下概率问题
3 通过分布函数求概率密度
法二:如果已知x,y相互独立
1 求联合概率密度f(x, y)(没讲独立,直接将x, z - x代入f(x, y)即可,讲独立,就可以不用求f(x, y))
2 积谁不换谁,换完求偏导加绝对值
3 确定被积函数f(x, z - x),确定x的范围,再通过y的范围经过还原确定z的范围
4 以x为横轴,z为纵轴作图,以z为横线讨论z的范围求f(z)
2.2 连续-离散
1 全概率公式分解
2 条件公式分解
