随机变量的数字特征
(一) 一维随机变量的数字特征
1 数学期望(可以理解为加权平均求和)
1.1 概念
(1) 离散型:X ~ \(P_i\)
\(E(X) = \sum_{i}^n x_ip_i\)(每一个正概率点是\(x_i\),对应的概率是\(p_i\),对应相乘后求和)
如果Y = g(x), \(E(Y) = \sum_{i}^{n}g(x_i)p_i\)
(2) 连续型:X ~ \(f(x)\)
\(E(X) = \int_{-\infty}^{+\infty}xf(x)dx\)(对于任意在正概率区间内的x,可以形成一个以底是dx,高是f(x)的小矩形,面积是f(x)dx,可以近似认为是x对应的概率,所以在整个区间上对所有的x积分就是\(\int_{-\infty}^{+\infty}xf(x)dx\))
如果Y = g(x), \(E(Y) = \int_{-\infty}^{+\infty}g(x)f(x)dx\)(Y= g(x),只是修改了定义域的范围,将定义域从x的范围变成了g(x)的范围,而对概率密度并没有影响)
1.2 性质
1.2.1 线性:E(aX + b) = aE(X) + b
1.2.2 独立:如果X与Y相互独立,才可以拆分E(XY) = E(X)E(Y)(也常用这个证明是否相互独立)
2 方差、标准差
2.1 概念:方差反应的是每个数据点对于均值的偏离情况,标准差就是方差开根号
\(D(X) = E((X - E(X)^2) = E(X^2) - (E(X))^2, \sigma = \sqrt{D(X)}\)
如果是求D(g(X)),或者说所有求D(X),都要利用定义转换成计算均值
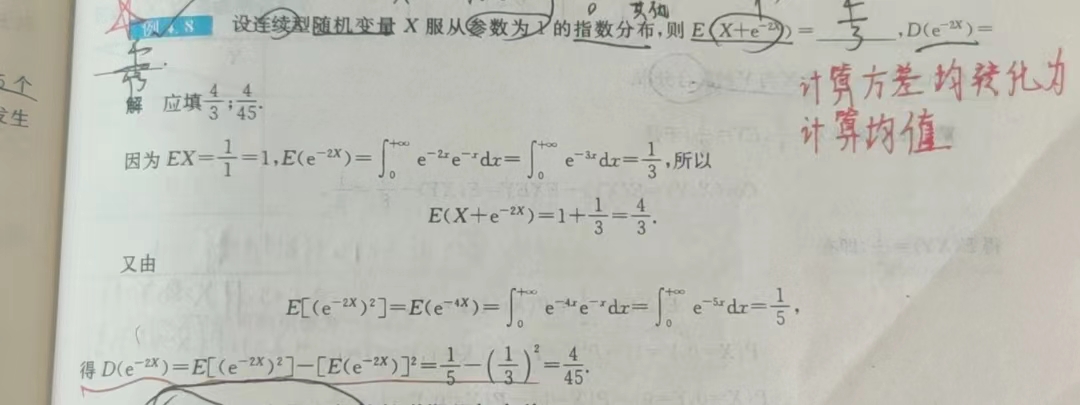
2.2 性质
2.2.1 \(D(aX + b) = a^2D(X)\)
2.2.2 \(D(X\pm Y) = D(X) + D(Y) \pm 2Cov(X, Y)\)
2.2.3 如果X与Y相互独立,\(D(aX + bY) = a^2D(X) + b^2D(Y)\)
3 切比雪夫不等式(偏离期望值的概率小,靠近期望值的概率大)
3.1 \(P\left\{|X - E(X)| < \epsilon \right\} \geq 1 - \frac{D(X)}{\epsilon^2}\)
3.2 \(P\left\{|X - E(X)| \geq \epsilon\right\} \leq \frac{D(X)}{\epsilon^2}\)
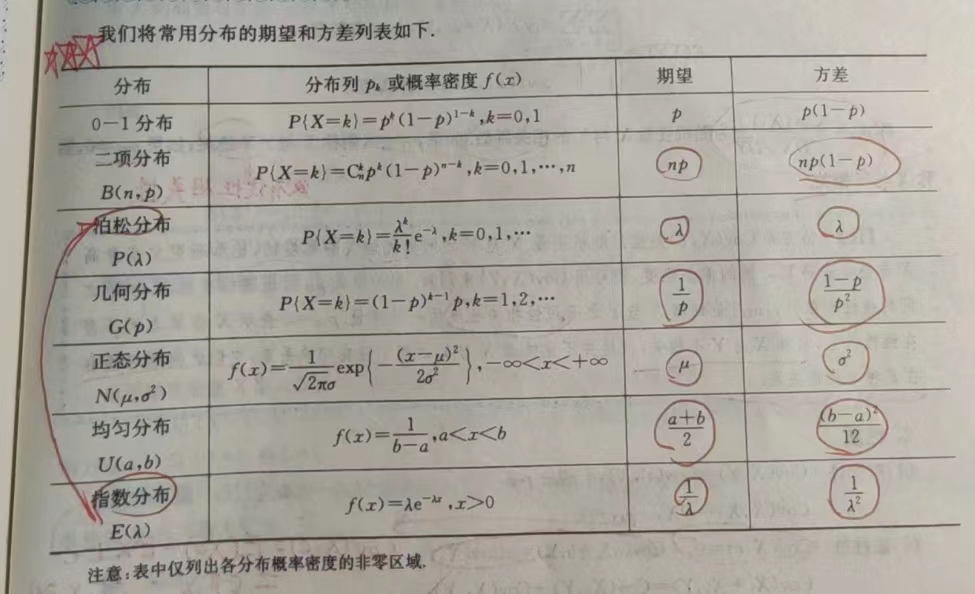
常用期望和分布
(二) 二维随机变量的数字特征
1 期望
1.1 离散型 \(E[g(X, Y)] = \sum_{i}\sum_{j}g(x, y)p_{i, j})\)(g(x, y)实际上代表的是平面定义域)
1.2 连续型 ,设(x, y)~f(x, y) \(E[g(X, Y)] = \iint_{-\infty}^{+\infty}g(x, y)f(x, y)dxdy\)
2 协方差与相关系数
1 概念:
协方差概念 Cov(X, Y) = E[(X - E(X))(Y - E(Y))] = E(XY) - E(X)E(Y)
相关系数概念 \(\rho_{XY} = \frac{Cov(X, Y)}{\sqrt{D(X)} \sqrt{D(Y)}}\)
如果\(\rho _{XY} = 0\),说明X与Y之间没有线性相关性,但可能有其他形式的相关,如果不为0,就是有线性相关性
2 性质(都可以从定义推出来)
2.1 对称性
2.2 线性性
典型题型
1 求二维连续型随机变量相关系数

求EX
求E(X^2)
求DX = E(X^2) - (EX)^2
Y同理
求E(XY)
利用相关系数公式

### 2 独立性与相关性的判定
#### 计算Cov(X, Y)
#### \(Cov(X, Y) \neq 0 \Rightarrow X与Y相关 \Rightarrow X与Y不相互独立\)
####\(Cov(X, Y) = 0 \Rightarrow X与Y不相关 \Rightarrow 通过构造事件组P\left\{X \leq a\right\}, P\left\{Y \leq a\right\}\)