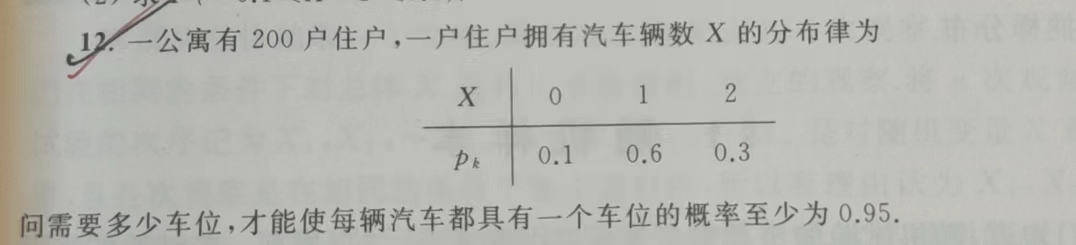
大数定律与中心极限定理
(一)依概率收敛
一:定义
鬼话:\(\forall \epsilon > 0, \exist N > 0, 当n > N时, 有\lim_{n \to \infty}P\left\{|X_n-a| < \epsilon\right\} = 1,则称X_n依概率收敛于a\)

人话:\(形容一列数X_n到点a的距离很近,极限状态下概率是1\)

题型:证明一个随机变量序列收敛



方法
1 构造Xn到一个数的距离小于ε
2 对上面构造的求极限,一般会向切比雪夫不等式靠近
(二)大数定律
1 切比雪夫
条件
(1) 变量序列相互独立
(2) 变量序列的方差存在且有上界
结论 \(\frac{1}{n} \sum_{i=1}^n X_i \overset{P}{\rightarrow} \frac{1}{n}\sum_{i=1}^{n}E(X_i)\) , 这堆变量序列的均值最终依概率收敛到这堆变量序列的期望们的均值
2 辛钦
条件
(1) 独立
(2) 同分布
(3) 期望存在
结论 \(\frac{1}{n}\sum_{i=1}^{n}X_i = \frac{1}{n}\sum_{i=1}^{n}E(X_i) = \frac{1}{n}nu = u\), 与切比雪夫结论类似,不过因为同分布所以\(E(X_i)一样\)
(三) 中心极限定理
条件
(1) Xi独立同分布于某种类型的分布
(2) Xi的期望和方差都存在,分别设期望是u,方差是σ^2
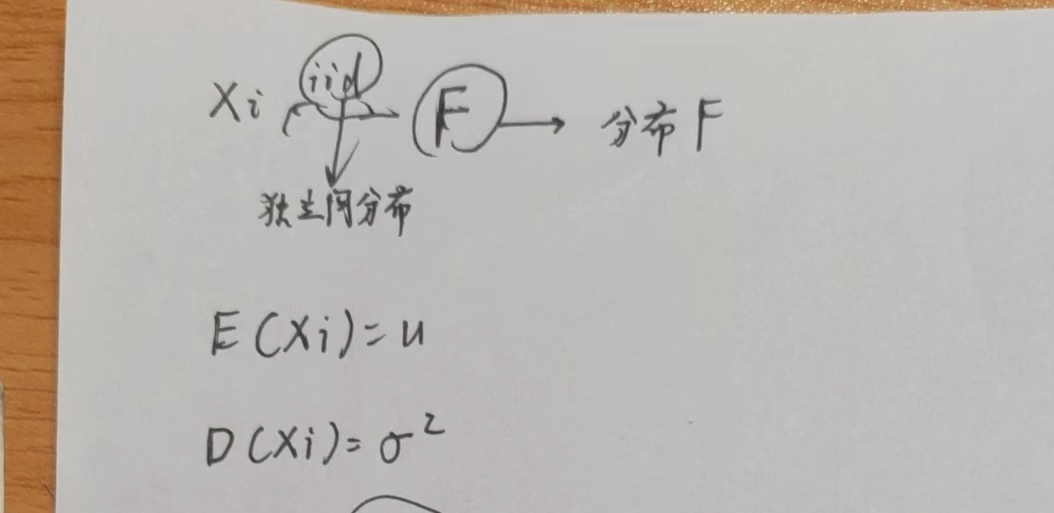
结论:对Xi求和再取极限(n->∞)就趋向于正态分布\(N(n\sigma, n\sigma^2)\)
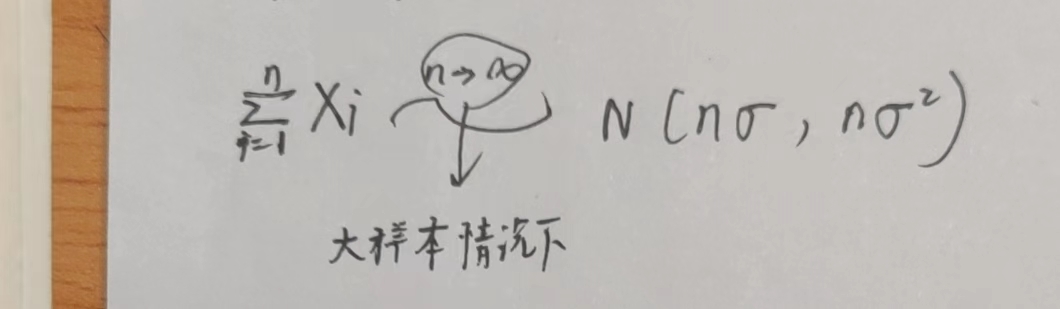
标准化的结论
1 \(\frac{(\sum_{i=1}^{n}X_i)-n\sigma}{\sqrt{n}\sigma} \sim N(0, 1)\)
2 \(\lim_{n\rightarrow\infty}P\left\{\frac{(\sum_{i=1}^{n}X_i)-n\sigma}{\sqrt{n}\sigma} \leq x\right\} = \Phi{(x)}\)

对于二项分布来说,其实每一次是一个0-1分布,所以均值是0-1分布的均值而不是二项分布的均值
题型:求一个范围A~B的概率
1 看一次取样满足于什么分布
2 求这种分布的均值u和方差σ
3 看取了几次样,作为n,得到近似正态分布\(N(nu, nσ^2)\)
4 A~B的概率就是\(Φ(\frac{B-nu}{σ}) - Φ(\frac{A-nu}{σ})\)