数理统计
总体与样本
总体:研究对象全体
样本:
1 n个(没有抽样)的\(X_i(i=1, 2, ……, n)\)
2 相互独立且同分布于某个随机变量X
3 组成的整体\((X_1, X_2, ……,X_n)\) 叫做一个样本,一次抽样结果的n个具体数值\((x_1, x_2, ……, x_n)\)叫做这个样本的观测值
样本的分布:如果样本\((X_1, X_2, ……, X_n)\)服从的X的分布函数是F(x),则\(F(x_1, x_2, x_n) = \prod_{i=1}^nF(x_i)\)(理解上就是相互独立所以可以拆分,另外什么概率密度,分布律类似)
举个例子
离散型
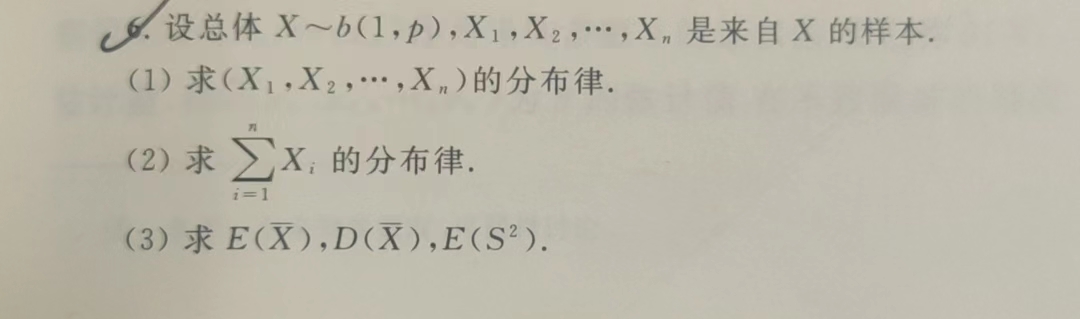
连续型

统计量及其分布
统计量
1 样本数字特征
样本均值: \(\overline{X} = \frac{1}{n}\sum_{i=1}^{n}X_i\)
样本方差,标准差:\(S^2 = \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline X)^2\), \(S = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline X)^2}\)
样本k阶原点矩: \(A_k = \frac{1}{n}\sum_{i=1}^{n}X_i^k(k = 1, 2, ……)\)
样本k阶中心矩: \(B_k = \frac{1}{n}\sum_{i=1}^{n}(X_i-\overline{X})^k\)
2 顺序统计量
最大顺序统计量:\(X_(n) = max\left\{X_1, X_2,……, X_n\right\}\)
分布函数:\(F_{(n)}(x) = [F(x)]^n\)
概率密度:\(f_(n)(x) = n[F(x)]^{n-1}f(x)\)(对上面F求导,注意是复合函数求导)
最小顺序统计量:\(X_{(1)}=min\left\{X_1, X_2, ……X_n\right\}\)
分布函数:\(F_{(1)}(x) = 1-[1-F(x)]^n\)
概率密度:\(f_{(1)}(x) = n[1-F(x)]^{n-1}f(x)\)
3 性质(\(设总体E(X)=\mu,D(X) = \sigma^2\))
\(X_i的期望与方差\)
\(E(X_i) = \mu\)
\(D(X_i) = \sigma^2\)
\(\overline{X}的期望与方差\)
\(E(\overline{X}) = E(X) = \mu\)
\(D(\overline{X}) = \frac{\sigma^2}{n}\)
\(S^2\)
\(E(S^2) = D(X) = \sigma^2\)
三大分布
1 \(\chi^2分布\)
1.1 定义:$ X_i独立同分布于N(0, 1),X = _{i = 1}{n}X_{i}2 ^2(n)$
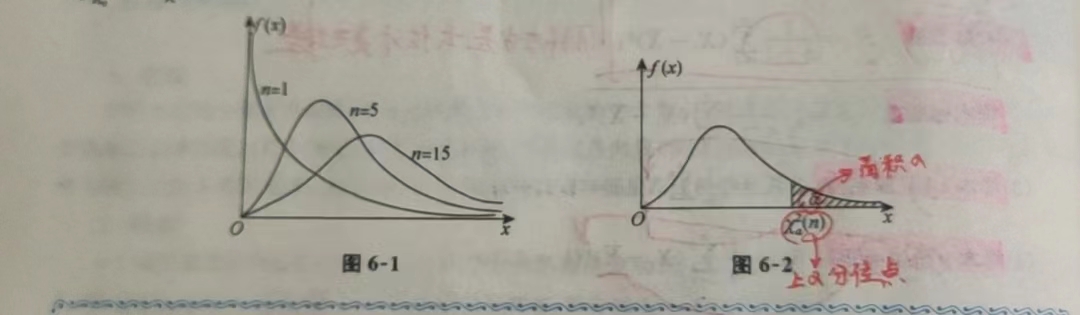
1.2 性质:
(1) \(若X_1 \sim \chi^2(n_1), X_2 \sim \chi^2(n_2), X_1与X_2相互独立,则X_1 + X_2 \sim \chi^{2}(n_1+n_2)\)
(2) \(若X\sim \chi^2(n),E(X)=n, D(X)=2n\)
2 t分布
2.1 定义:\(X\sim N(0, 1), Y\sim \chi^2(n), X与Y相互独立,t = \frac{X}{\sqrt{\frac{Y}{N}}} \sim t(n)\)
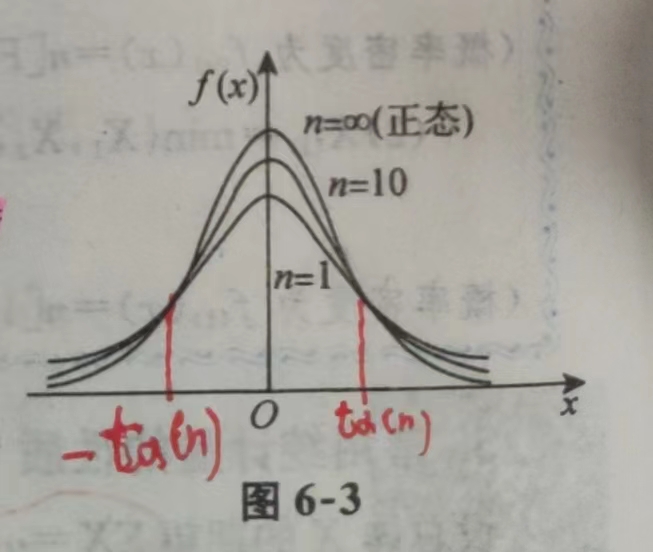
2.2 性质: \(图形关于y轴对称,所以t_{\alpha}(n)(这个点右侧面积是\alpha) = -t_{1-\alpha}(n)(这个点右侧面积是1-\alpha)\)
3 F分布
3.1 定义:\(X\sim \chi^2(n_1), Y\sim \chi^2(n_2),X与Y相互独立,F = \frac{X/{n_1}}{Y/{n_2}}\sim F(n_1, n_2)\)
3.2 性质
(1) \(若F\sim F(n_1, n_2),则\frac{1}{F}\sim F(n_2, n_1)\)
(2)\(若F_{1-\alpha}(n_1, n_2) = \frac{1}{F_{\alpha}(n_2, n_1)}\)
题型:给一个不标准的分布,去表示出一个标准的分布



\(X_1, X_2,……X_n独立同分布正态(N(\mu, \sigma^2))时常用结论\)(这些结论常用于后面区间估计和假设检验)
(1) \(\overline{X}\sim N(\mu, \frac{\sigma^2}{n})(从前面\overline{X}的均值与方差可知),所以\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim N(0, 1)\)
(2) \(\sum_{i=1}^{n}(\frac{X_i-\mu}{\sigma})^2 \sim \chi^2(n)(X_i标准化后的平方和服从与\chi^2)\)
(3) \(\sum_{i=1}^{n}(\frac{X_i-\overline{X}}{\sigma})^2 = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2(n-1)(上面如果总体期望未知,可以用样本均值代替后做相应改动)\)
(4) \(\frac{(\overline{X}-\mu)}{S/\sqrt{n}} \sim t(n-1)(将(1)中的总体标准差\sigma用样本标准差S替换), \frac{n(\overline{X}-\mu)^2}{S^2} \sim F(1, n-1)\)
举个例子

(1)先确定要表示的分布
(2)将要表示的分布里的标准分布通过题干中分布标准化后换元表示
参数的区间估计
首先需要了解一些基本概念:
\(\mu\):表示期望,不随抽样改变而改变
\(\overline{X}\):均值,由每次抽样决定
均值虽然不是期望,但一般来说均值与期望之间距离\(|\overline{X}-u|\)比较小的概率还是很大的,公式表示就是
\(P\left\{|\overline{X}-\mu| \leq \varepsilon \right\} = 1 - \alpha\)
其中\(\alpha\)叫显著性水平,\(1-\alpha\)叫置信区间
\(\sigma^2已知时的置信区间:(\overline{X}-z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}}, \overline{X}+z_{\frac{\alpha}{2}}\frac{\sigma}{\sqrt{n}})\)
证明:
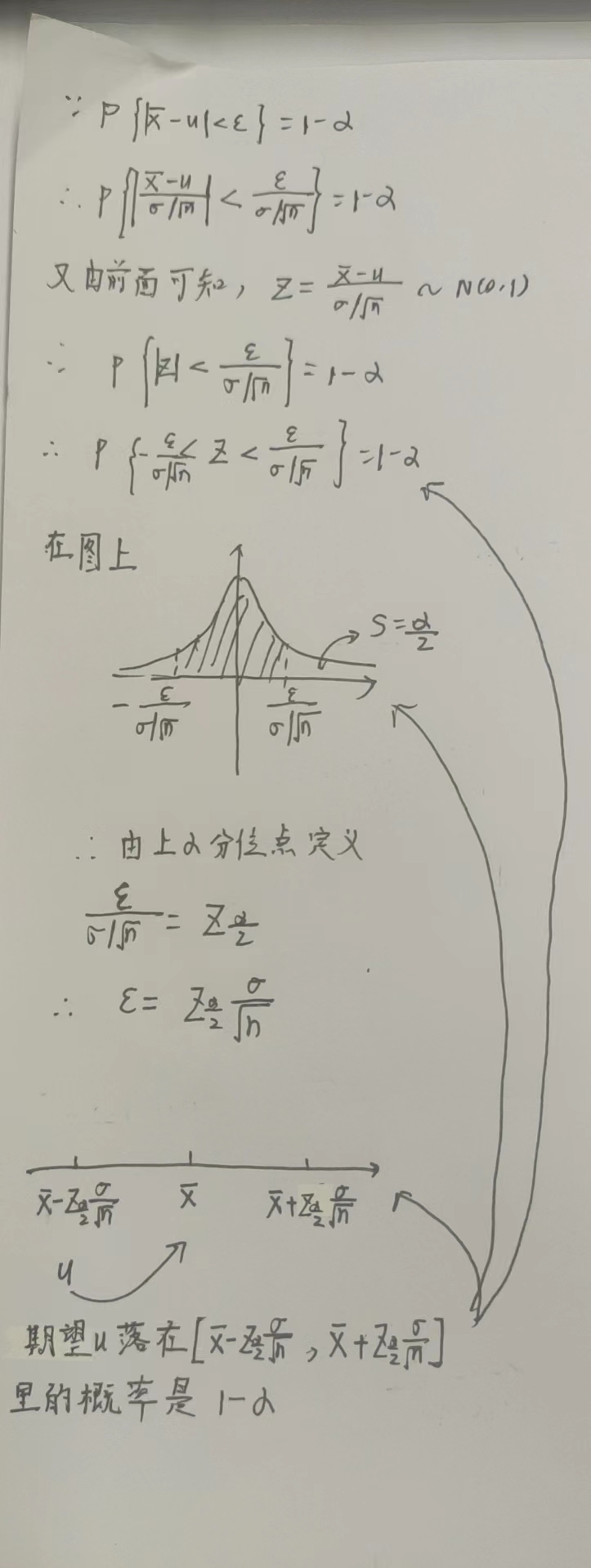
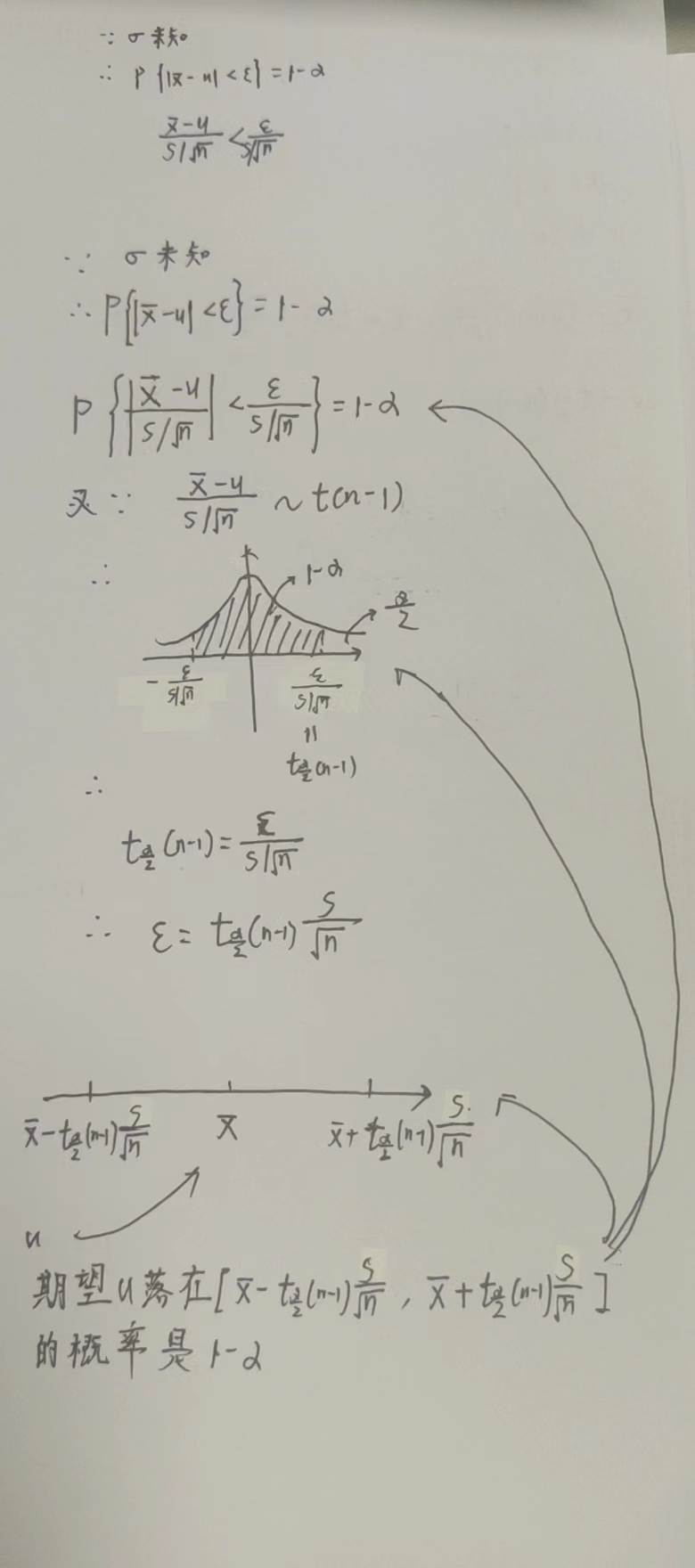
\(\sigma^2未知时的置信区间:(\overline{X}-t_{\frac{\alpha}{2}}(n-1)\frac{S}{\sqrt{n}}, \overline{X}+t_{\frac{\alpha}{2}}(n-1)\frac{S}{\sqrt{n}})\)
证明
举个例子

假设检验(u只是一个假设的值,在求出拒绝域后,看实际得到的结果落在哪里,如果落在拒绝域说明假设不成立)
基本思想是\(P(\overline{A}) = 1 - P(A)\)
拒绝域:拒绝原假设\(H_0\)的全体样本点组成集合
接受域:接受原假设\(H_0\)的全体样本点组成集合
1 双边检验(\(分布的下标是\frac{\alpha}{2}\))
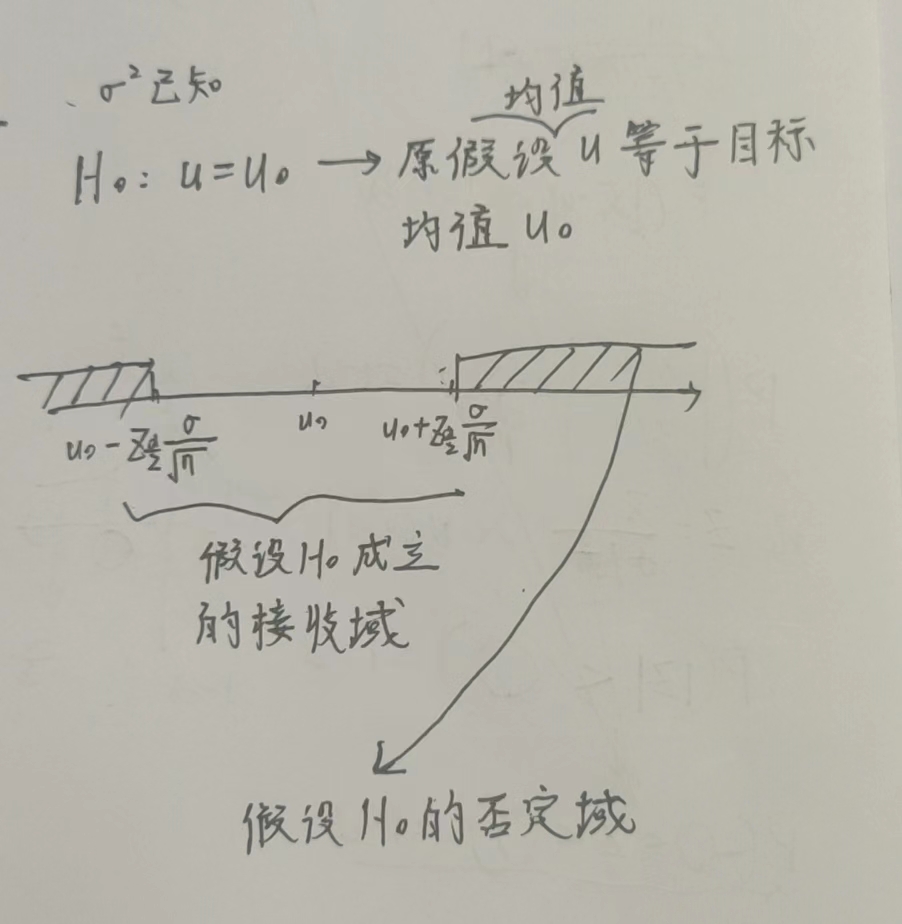
(1) \(\sigma^2已知\)
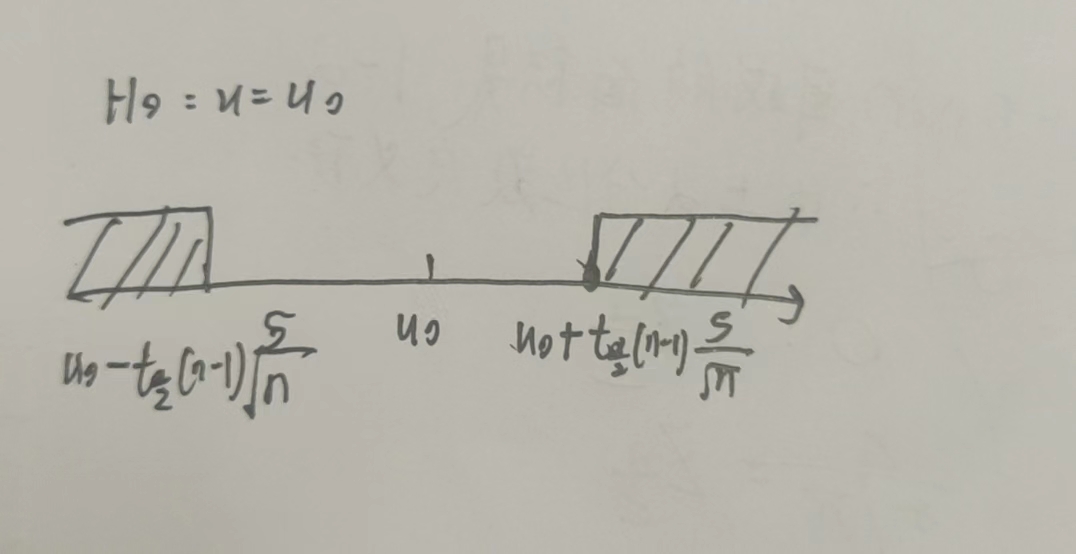
(2) \(\sigma^2未知\)
2 单边检验($分布的下标是$)
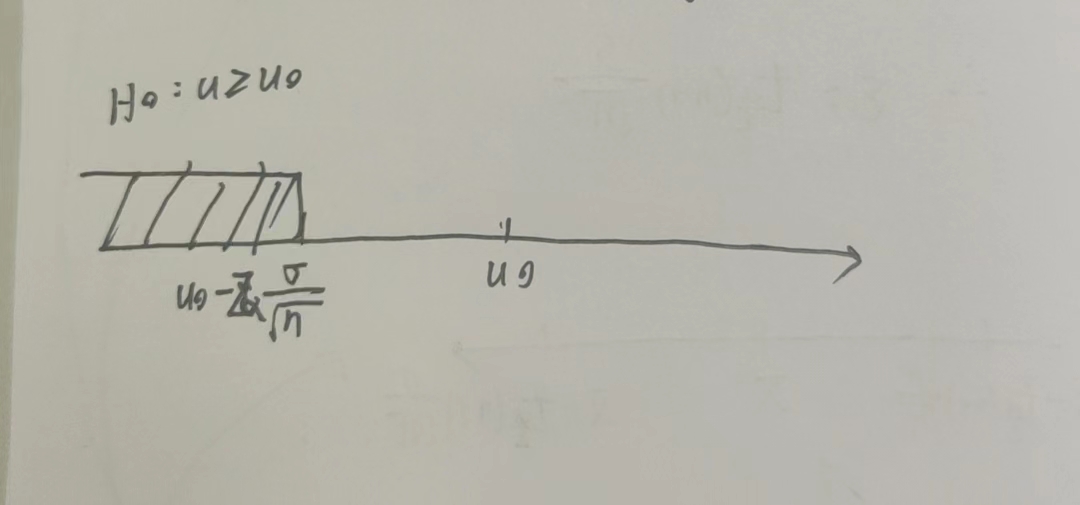
(1) \(\sigma^2已知\)
\(\mu \leq u_0\)
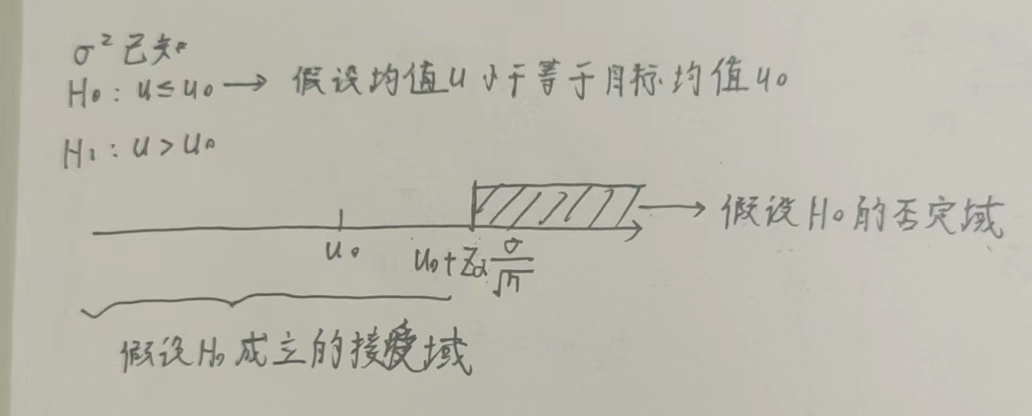
\(\mu \geq u_0\)
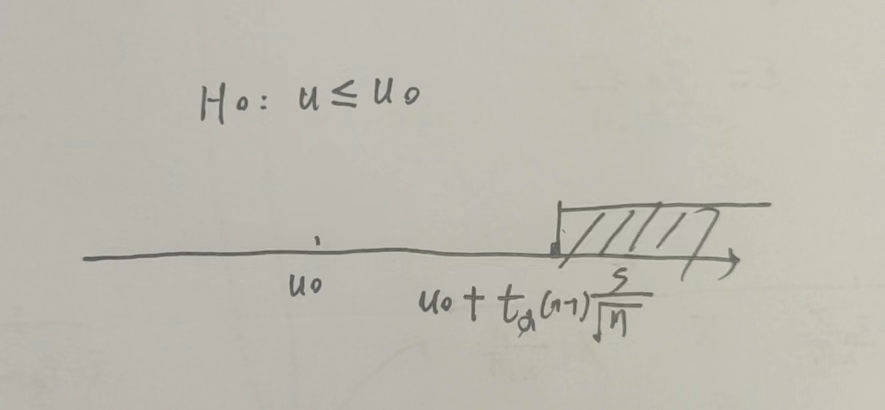
(2)\(\sigma^2未知\)
\(\mu \leq u_0\)
\(u \geq u_0\)
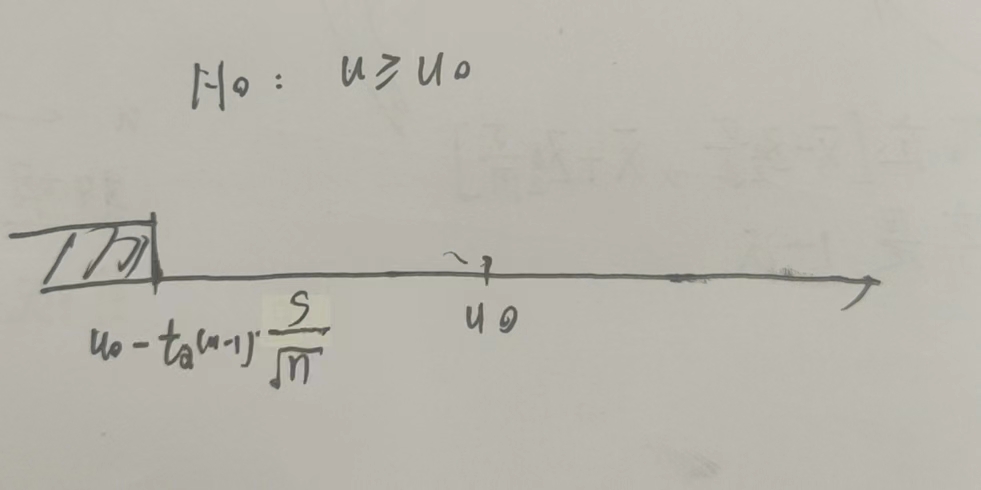
举个例子

参数的点估计
方法
矩估计法:\(样本中有未知值\theta,用样本均值等于总体期望E(X) = \overline{X}来计算\theta的估计值\hat{\theta}\)
1 \(求E(X)\)
2 \(另E(X) = \overline{X}\)
最大似然估计法 \(如果是离散型,概率分布中含\theta,如果是连续型,概率函数含\theta,即后面所求将是包含\theta的函数\)
(1) \(将样本中所有结果相乘得到L(\theta) = \prod_{i=1}^nP\left\{X_i = x\right\}\)
(2) 第一步得到的等式两边取对数
(3) \(等式两边关于\theta求导,并另之为0\)
举个例子
离散型

矩估计法

最大似然估计法

连续型

矩估计法
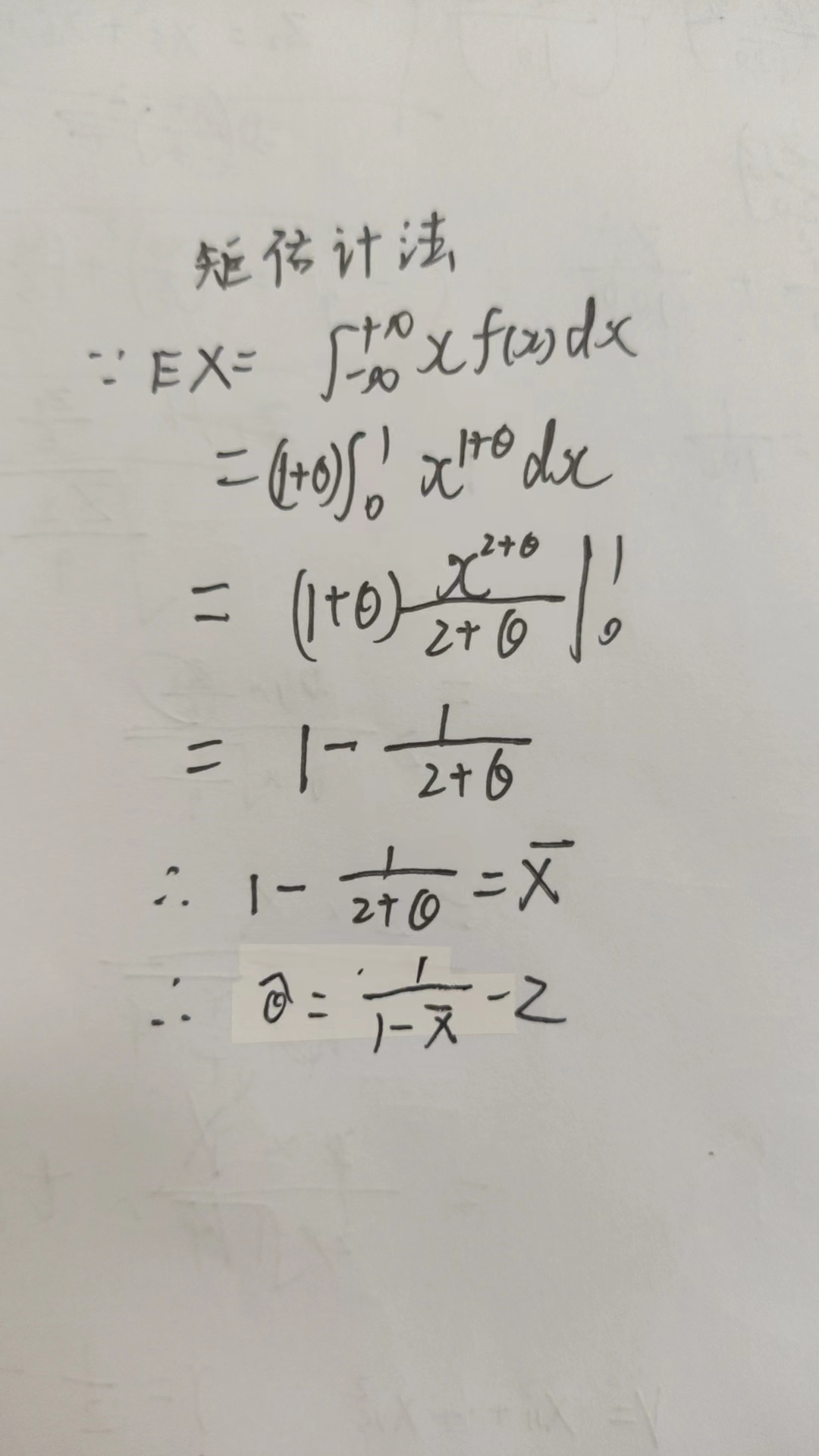
最大似然估计法
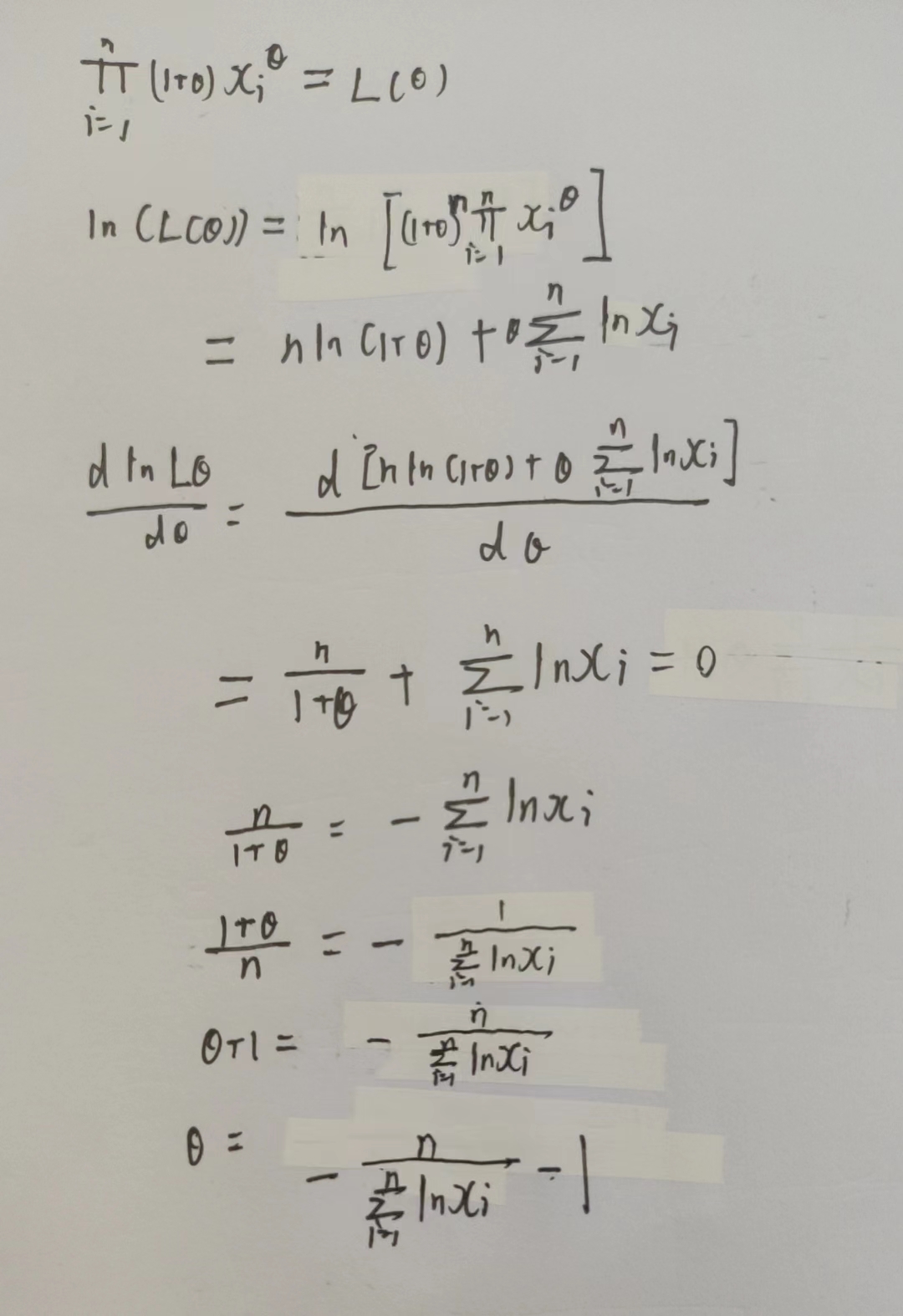
估计量的评价标准
无偏性:\(得到\hat{\theta}后证明E(\hat{\theta}) = \theta\)
举个例子
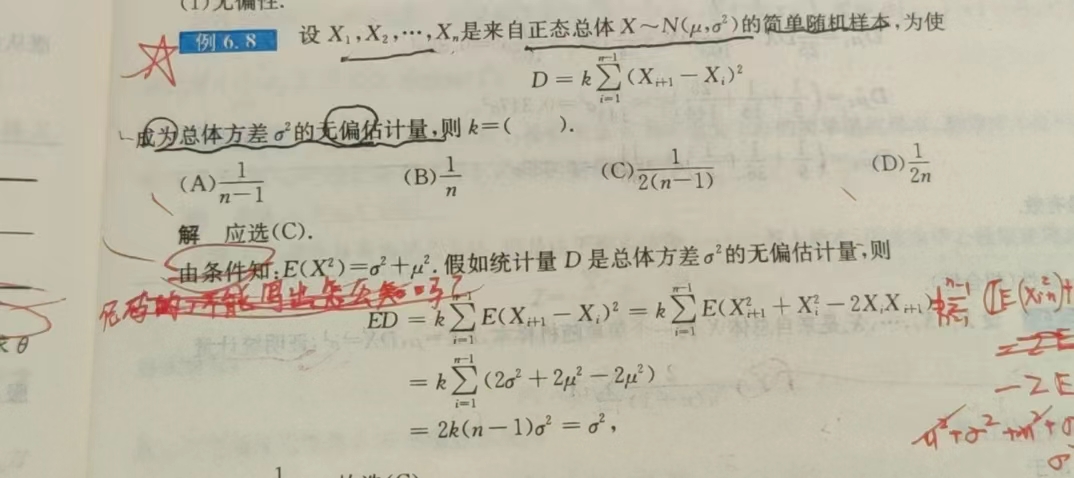
有效性:\(比较哪个D(\hat{\theta})更小\)
举个例子

一致性(相合性):\(证明\hat{\theta}依概率收敛于\theta,即\lim_{n\rightarrow\infty}P\left\{|\hat{\theta}-\theta| < \epsilon\right\} = 1\),使用时往往结合切比雪夫不等式
举个例子

两类错误
以有没有病举例
$P{拒绝H_0|H_0为真} = $ 有病但被判成无病的概率
\(P\left\{接受H_0|H_0为假\right\}\) 无病但被判成有病的概率
举个例子
