随机事件与概率

事件的关系与运算

一：关系

1 包含

2 相等

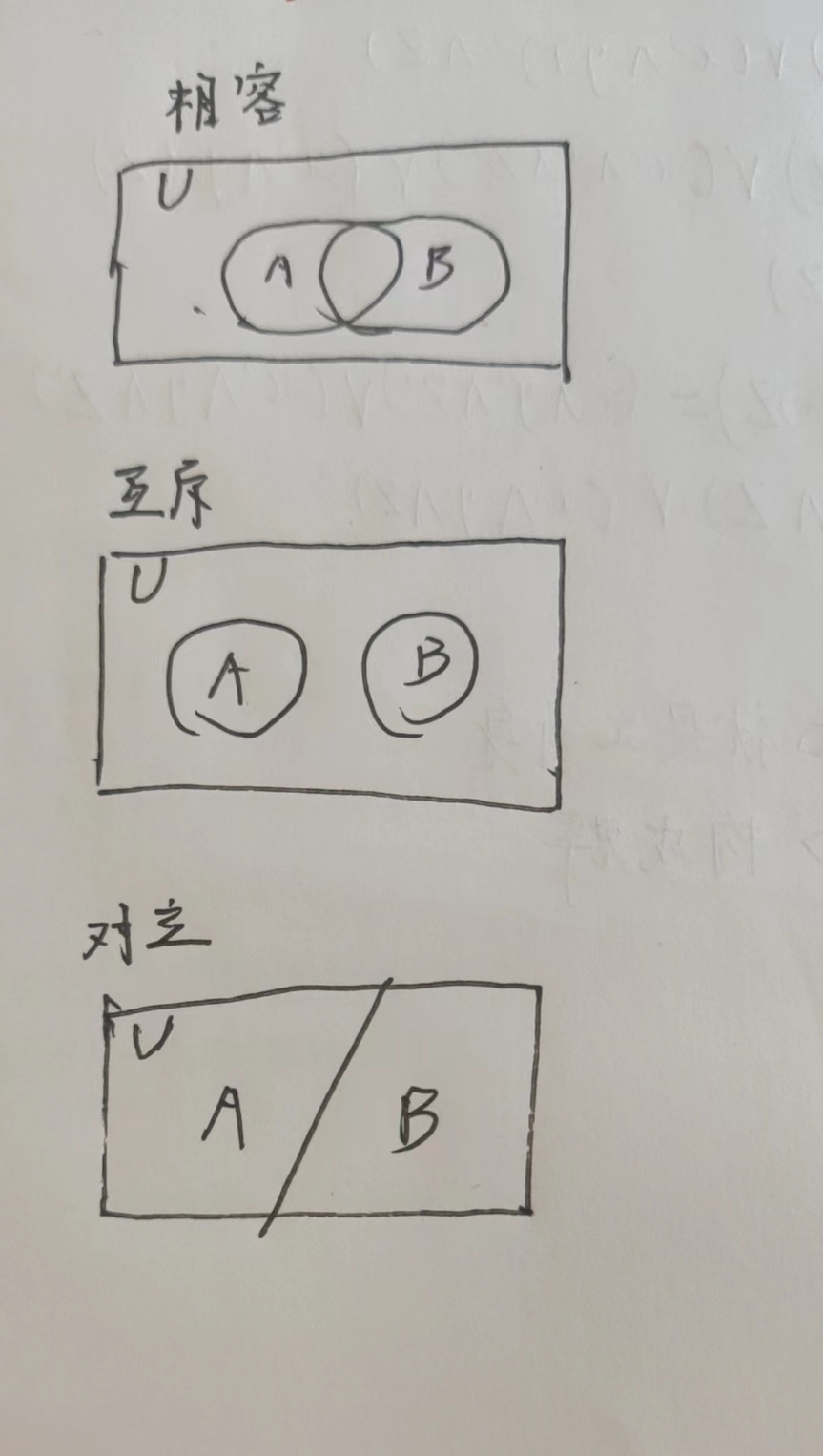
3 相容：AB \(\not=\) \(\emptyset\)

4 互斥：AB = \(\emptyset\)

5 对立：\(\overline{A}\)

举例

二：运算

运算类型

1 并

2 交

3 差

运算律(均只针对交并运算)

1 吸收：若A\(\subset\)B,则A\(\bigcup\)B = B, A\(\bigcap\)B = A

2 交换

3 结合

4 分配

5 德摩根:长杠变短杠，开口换方向、

题型

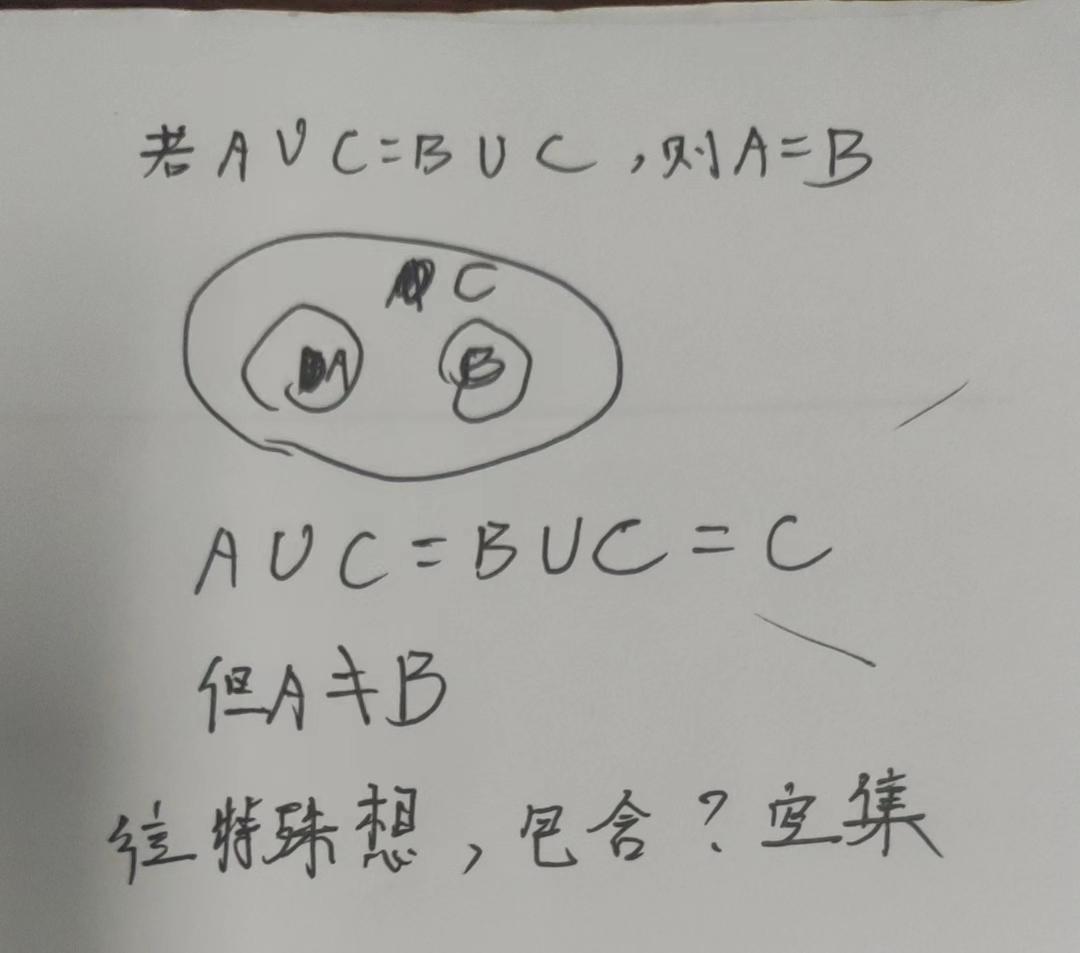
题型一：判断命题是否成立

法一：画文氏图

法二：公式推理

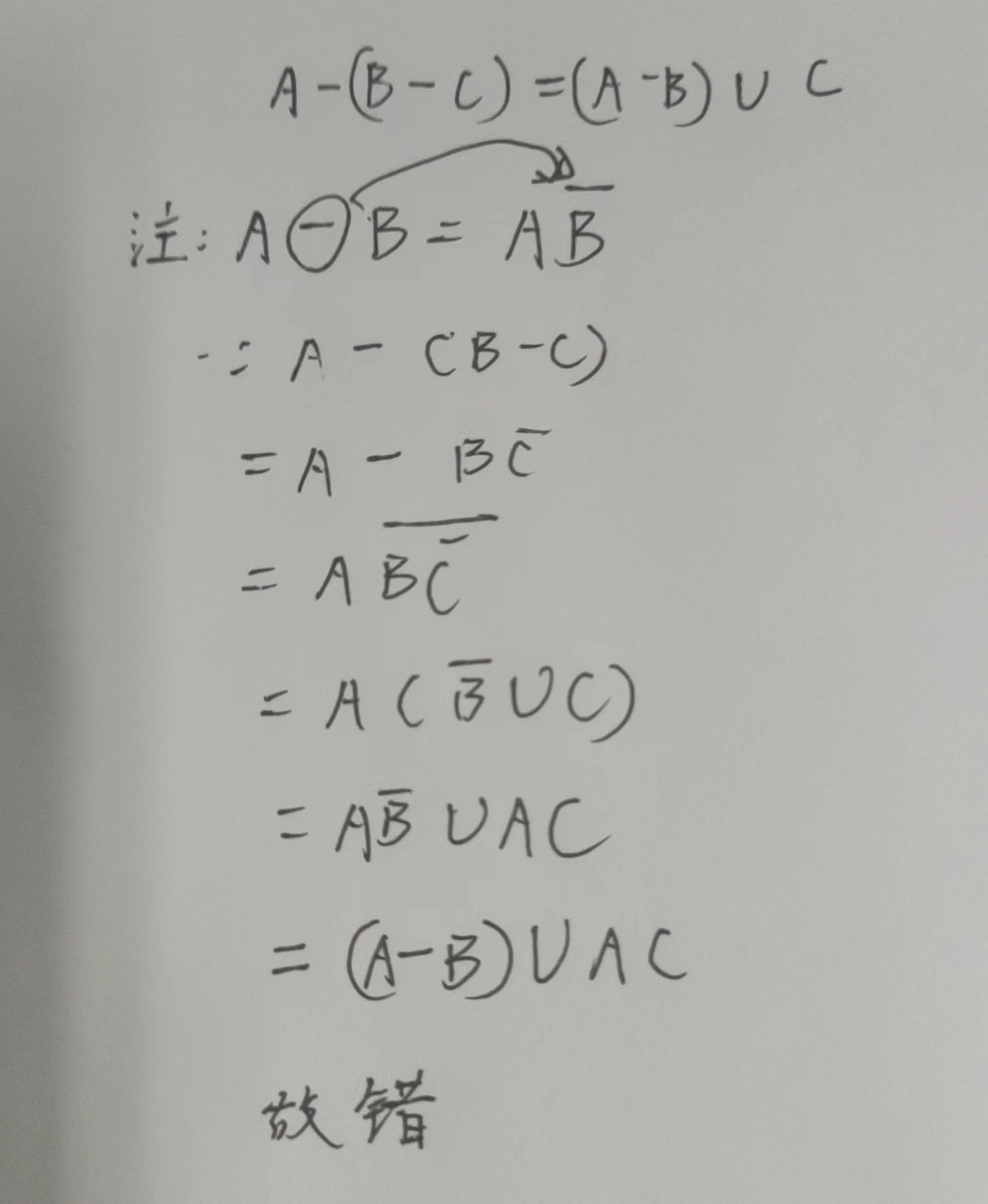
题型二：关于“至少”这个事件

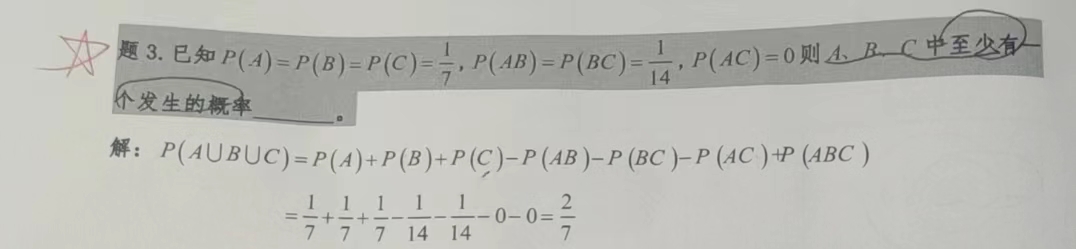
A，B中至少有一个发生\(\Leftrightarrow\)A∪B

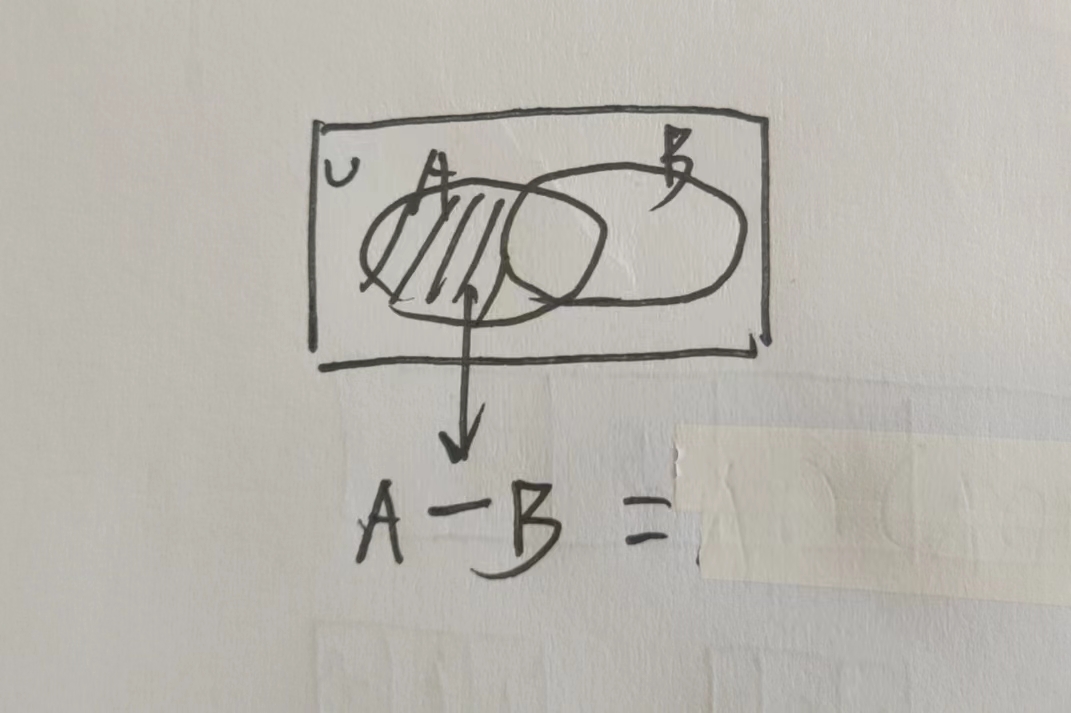
A - B ↔︎ A\(\overline{B}\) ↔︎ A - AB

古典概型和几何概型

一 古典概型

1 排列：从n个元素中取出m个排成一列，所有排列的个数 P，第一个有n种取法，第二个有n - 1种取法……第m个,前面已经选了(m - 1)个，还剩n - (m - 1)个，所以有n - m + 1种取法

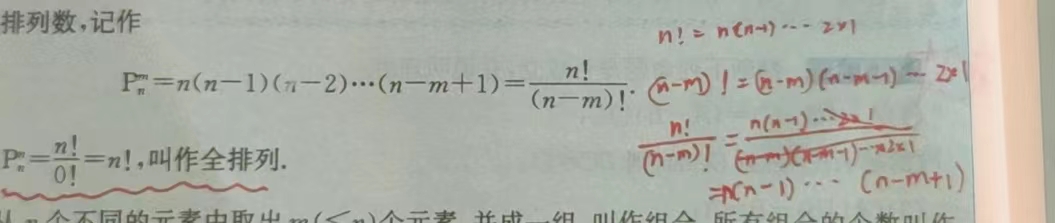
2 组合：从n个元素里挑m个成一种组合，因为m个元素有m!中排列方式，而组合只选择其中一种

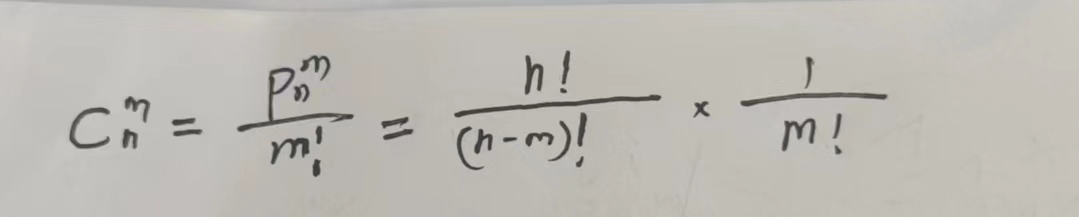
3 题型

3.1 随机分配：将n个质点放到N个盒子里

(1) 盒子容量不限制：每个质点有N个选择，分法总数 = n^N

(2) 盒子最多放一个：第一个质点有N种选择，第二个质点有N-1种选择，……最后一个前面已经选了n - 1个盒子，剩下N - (n - 1)个盒子的选择，即是P_n^m

3.2 简单随机抽样：从盒子N个里抽n个

(1) 有放回：每次都有N个选择，一共n^N

(2) 无放回：第一次有N种选择，第二次有N-1种选择，……最后一个前面已经选了n - 1个，剩下N - (n - 1)个的选择，即是P_n^m

(3) 一口气取：无放回的是排列，一口气取的是组合

二 几何概型：常见面积问题

概率的基本性质与公式

一 性质

1 有界性：任何一个时间的概率在0~1(0与1都能取得到)

2 单调性：若A\(\subset\)B,则P(B- A) = P(B) - P(A)

3 逆概率公式：P(\(\overline{A}\)) = 1 - P(A)

二 公式

1 加法公式(多个字母的并事件)：奇数个字母前面是正号，偶数个字母前面是负号，然后组合排列出所有情况

2 减法公式：P(A - B) = P(A) - P(AB)

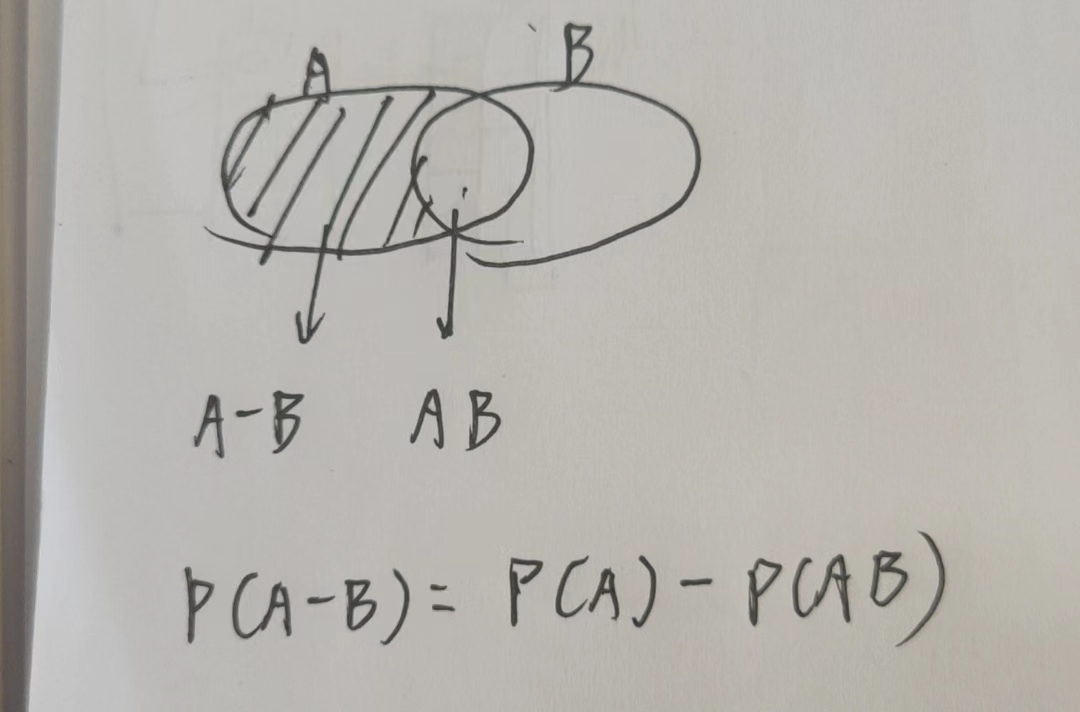
题型： (1) 常在AB 和 A\(\bigcup\)B上做文章

2. 前面公式要熟记

微信图片_20231210144201

3 条件概率公式

4 全概率公式(由因推果，多重因素A_i导致事件B发生，求事件B发生的概率)

4.1 完备事件组的全集分解

4.2 加法公式的互斥

4.3 条件概率公式

举例：

嵌套：

5 贝叶斯公式(由果索因，已知事件B发生，求是因素A_i导致其发生的概率)

举例：

结合全概率公式使用

事件的独立性

两两独立与相互独立

定义

题型

性质：如果若干个事件相互独立，则其中一部分事件与另一部分事件的运算生成的新事件与另一部分事件运算生成的新事件仍然相互独立

题型

​