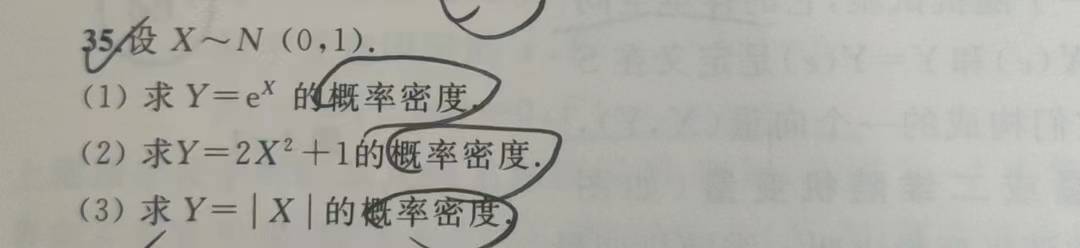
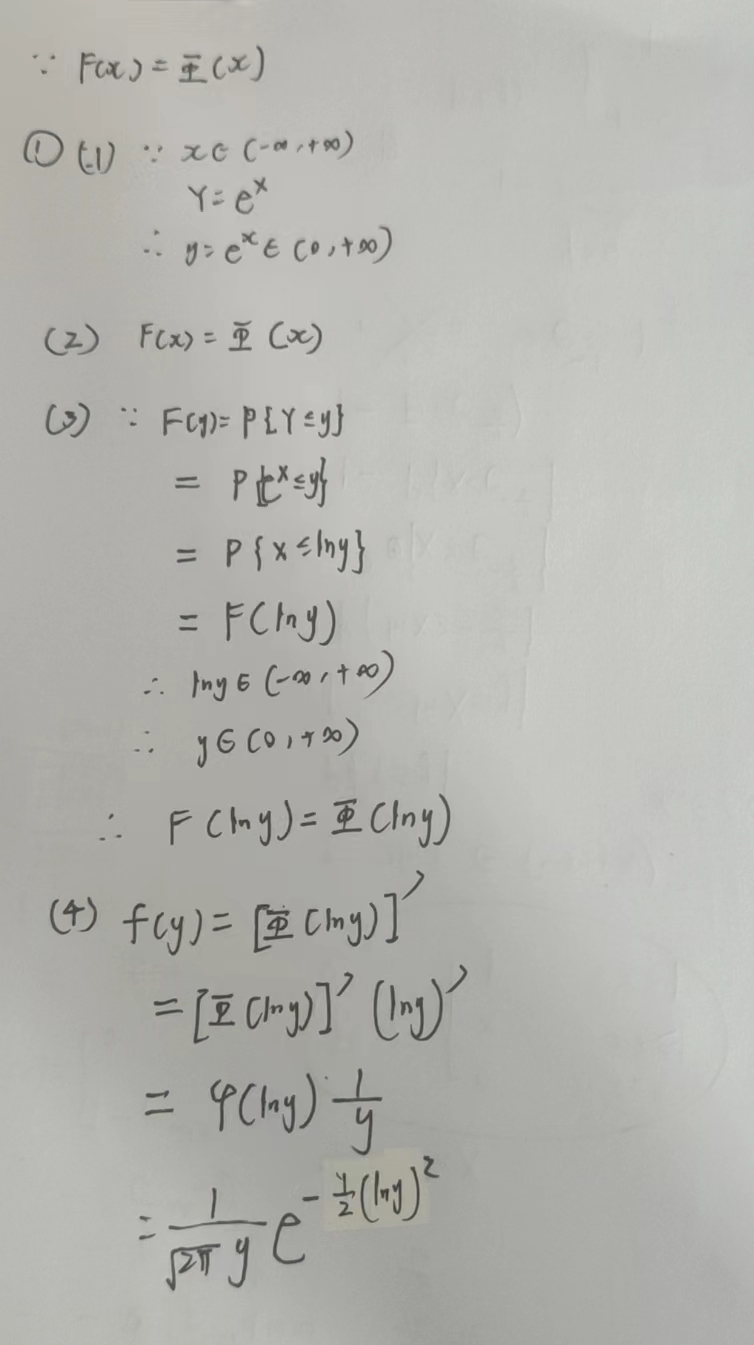一维随机变量及其分布
(一) 一维随机变量分布函数
1 概念:F(x) = P{X \(\leq\)x}
题型

注意求X的分布函数,F(x) = P{X \(\leq\) x} = \(\int_{\infty}^{x} f(x)\, dx\)(因为这里是连续型)
2 性质
2.1 单调不减
2.2 右连续
2.3 向负无穷取极限是0,想正无穷取极限是1
3 应用:求概率
3.1 P{X \(\leq\) a} = F(a)
3.2 P{X < a} = F(a - 0)(左极限)
3.3 P{X = a} = F(a) - F(a - 0)
(二) 一维离散型
1 分布律:将每一个正概率点(不一定值是正,而是对应概率值是正的点) 与其对应的概率做成表格
第一行:每个正概率点的值
第二行:每个正概率点对应的概率

2 分布函数F(x):对所有小于x的正概率点求和,常成阶梯状
3 应用:求概率,说白了就是将区域内所有正概率点求和,比如求P{a < X < b}
从分布律角度,就是将a~b范围内所有正概率点求和
从分布函数角度,就是F(b - 0) - F(a)
4 常见分布
4.1 n重伯努利分布(n, p)
n:重复实验次数
p:一次实验中成功的概率(每次实验只有两种结果)
分布律
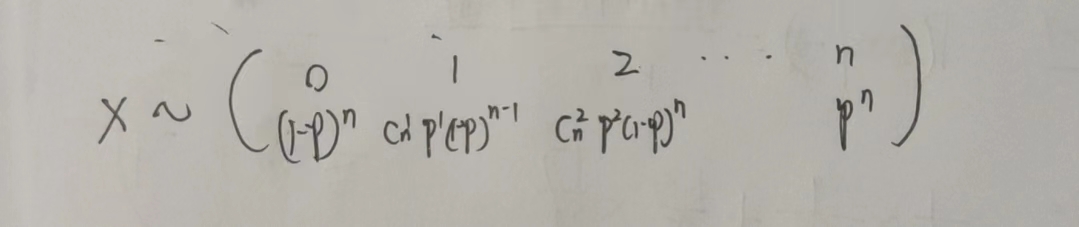
n重伯努利分布里几种特殊的分布
(1) 0 - 1分布:就取1次
(2) 几何分布:前(n - 1)次都没中,第n次中
举例

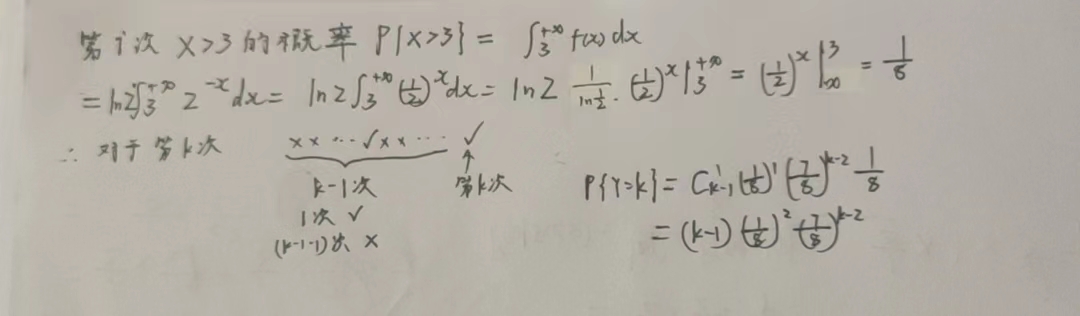
4.2 超几何分布:好的坏的混在一起,一共有N个,其中好的有M个,取n个,n个里面有k个好的,(n - k)个坏的

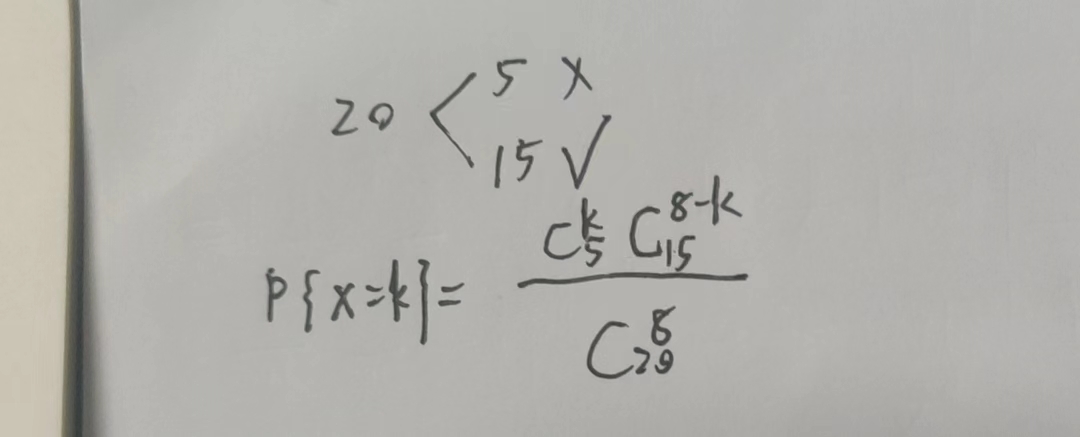
4.3 泊松分布
公式

性质 \(\lambda\) = np


上面这道题计算要用到\(\lambda\) = np
(三) 一维连续型
1 概率密度f(x)
2 分布函数:F(x) = \(P\left\{X\leq\ x \right\} = \int_{-\infty}^{x} f(x)\, dx\)
3 应用:求概率,说白了就是对在指定区域的f(x)求积分
4 主要分布
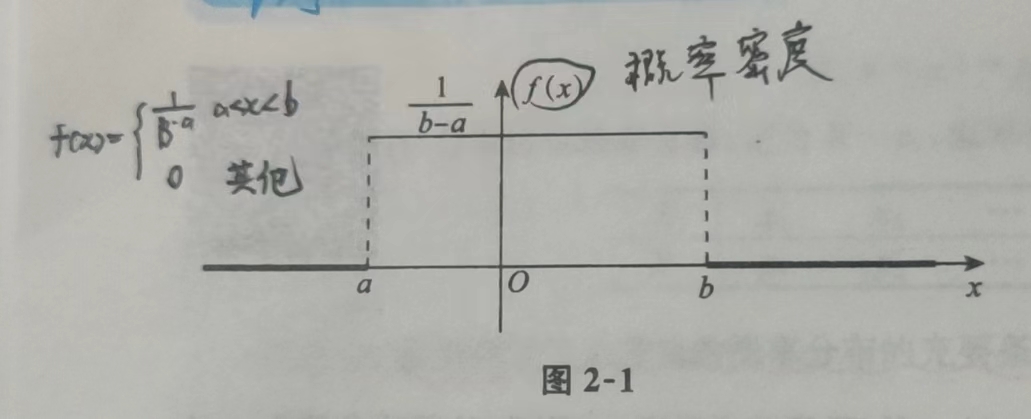
4.1 均匀分布U(a, b)
概率密度
分布函数
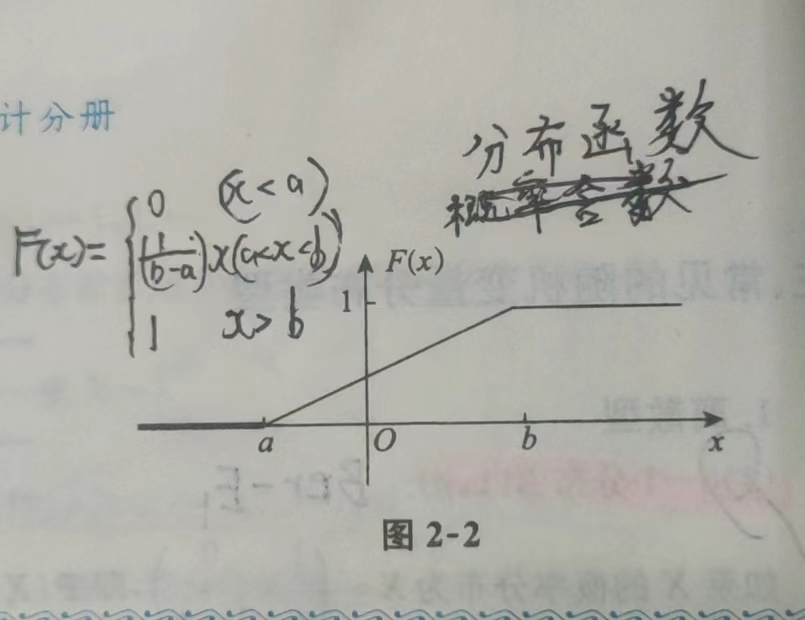
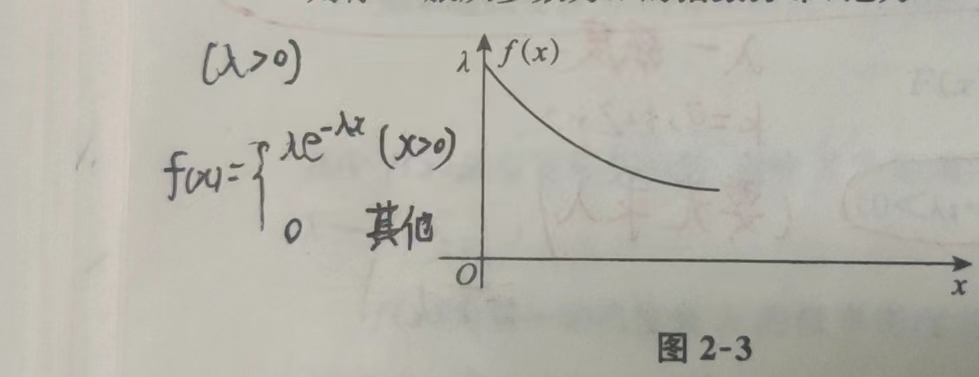
4.2 指数分布E(\(\lambda\))(指数分布具有无记忆性)
概率密度
分布函数
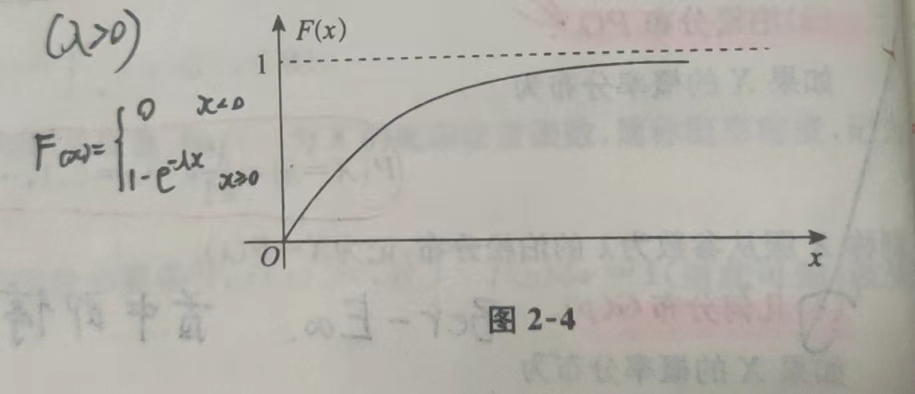
题型:

4.3 正态分布N(u, σ2)
概率密度
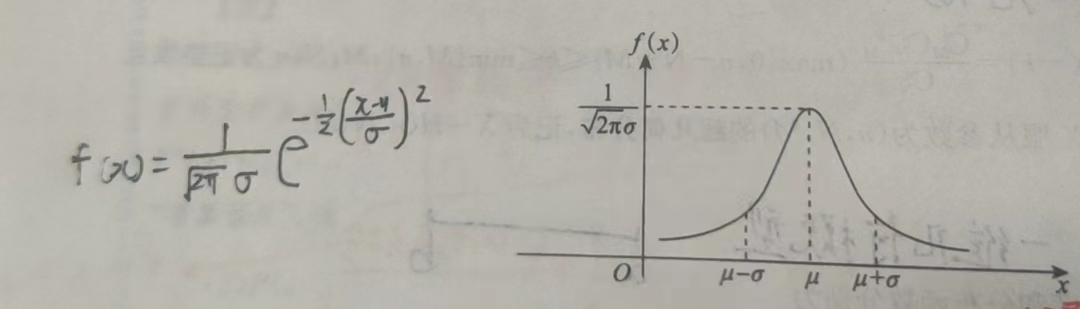
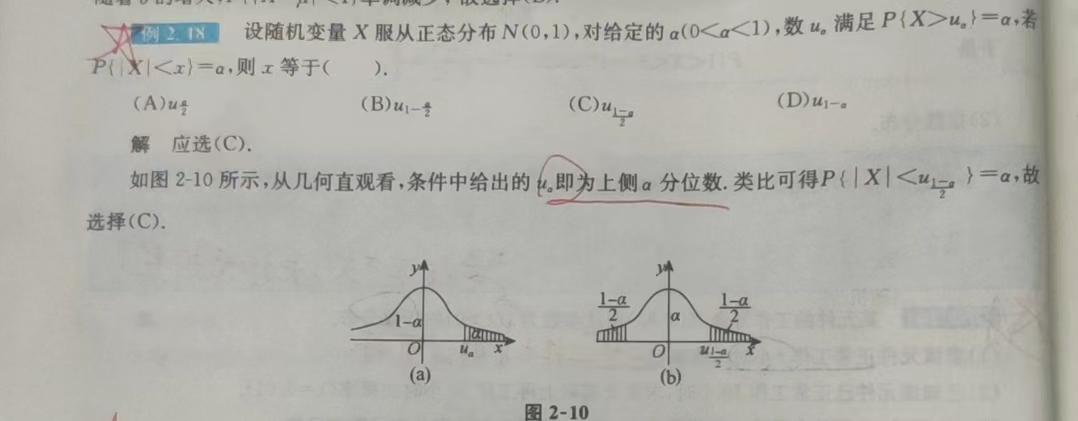
上\(\alpha\)分位数u\(\alpha\):使点\(\alpha\)右侧φ的面积是\(\alpha\),计算出\(\alpha\)右侧面积就是下标\(\alpha\)
举例
标准正态分布N(0, 1)
概率密度\(\phi\)(x)
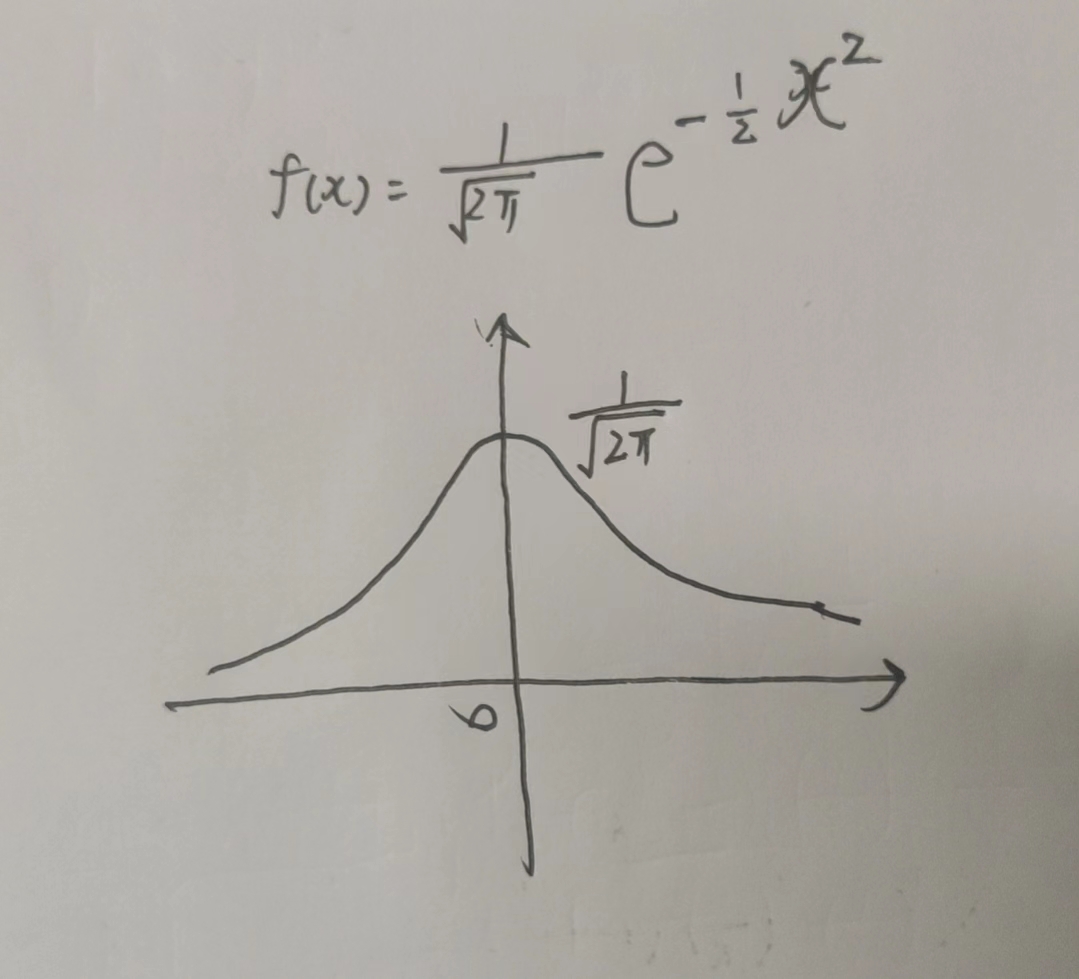
分布函数:只用记住是\(\Phi\)(x)就行,性质围绕其奇偶性展开

标准化(所有有关正态分布不等式的判别都要标准化)
题型

换元标准化

性质
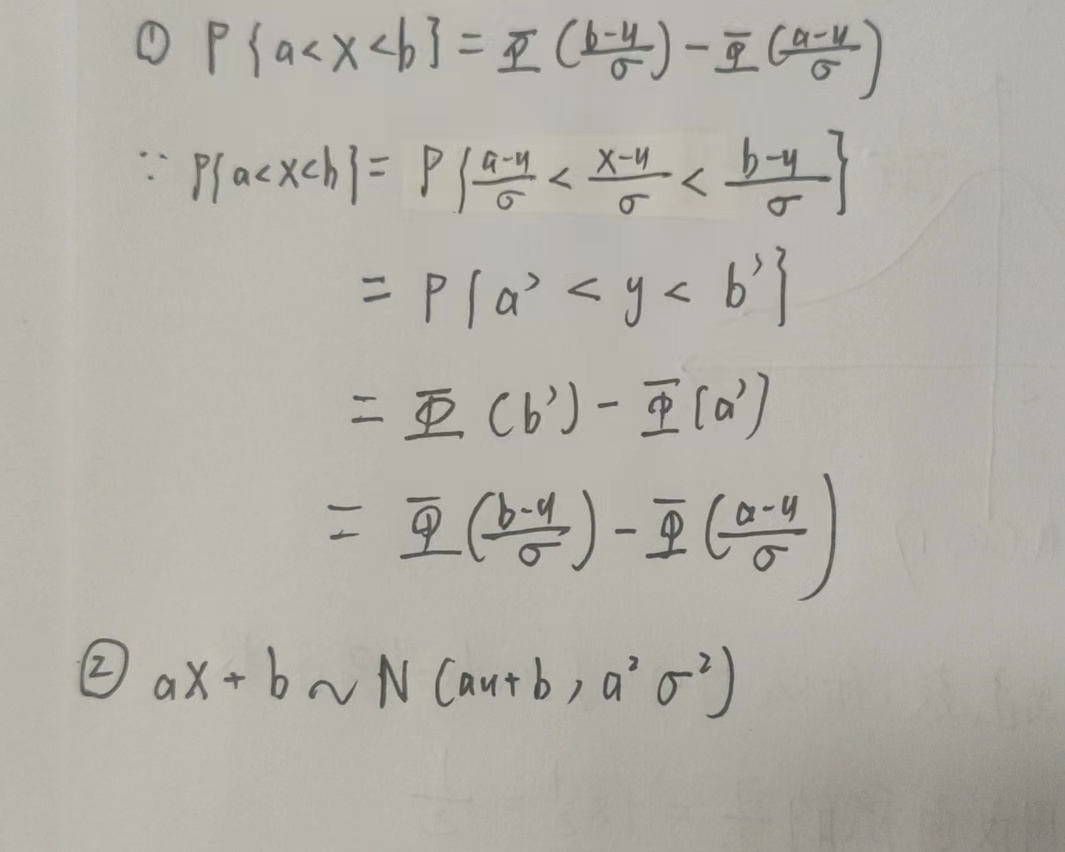
(四) 典型题型:一维随机变量函数的分布,已知一种随机变量的概率分布f(x),通过某种函数变换得到另一种函数Y, 求f(y)的概率分布
1 根据函数变换Y = g(X)得y = g(x),代入x的范围得到y的范围作为Y的定义域
2 求出F(x)的分布函数
3 利用定义F(y) = P{Y\(\leq\)y},将Y用X代入,转化为P{X \(\leq\)h(y)}后将h(y)代入F(X)得到F(h(y))和定义域(因为F(x)一般是分段函数,所以也要将h(y)代入到分段的定义域里得到新的分段定义域)
4 对F(y)求导得到概率分布f(y)
开胃小菜

难度加强