一些基础
扩展结点:一个正在产生儿子的结点称为扩展结点
活结点:一个自身已生成但其儿子还没有全部生成的节点称做活结点
死结点:一个所有儿子已经产生的结点称做死结点
深度优先的问题状态生成法:如果对一个扩展结点R,一旦产生了它的一个儿子C,就把C当做新的扩展结点。在完成对子树C(以C为根的子树)的穷尽搜索之后,将R重新变成扩展结点,继续生成R的下一个儿子(如果存在)
回溯法:为了避免生成那些不可能产生最佳解的问题状态,要不断地利用限界函数(bounding function)来处死那些实际上不可能产生所需解的活结点,以减少问题的计算量。具有限界函数的深度优先生成法称为回溯法
子集树和排列树
子集树
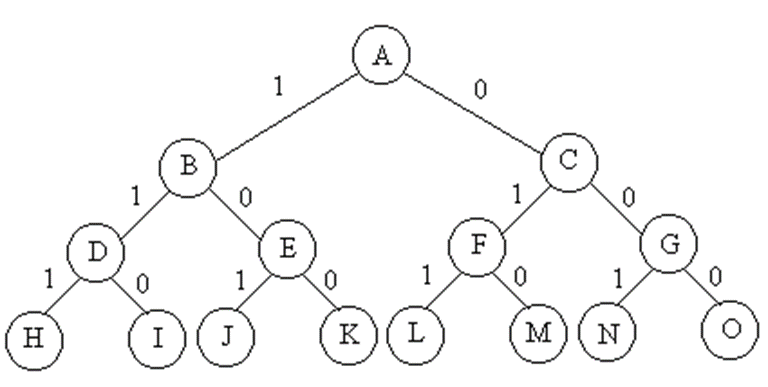
遍历子集树需\(O(2^n)\)计算时间
1 | void backtrack (int t) |
排列树
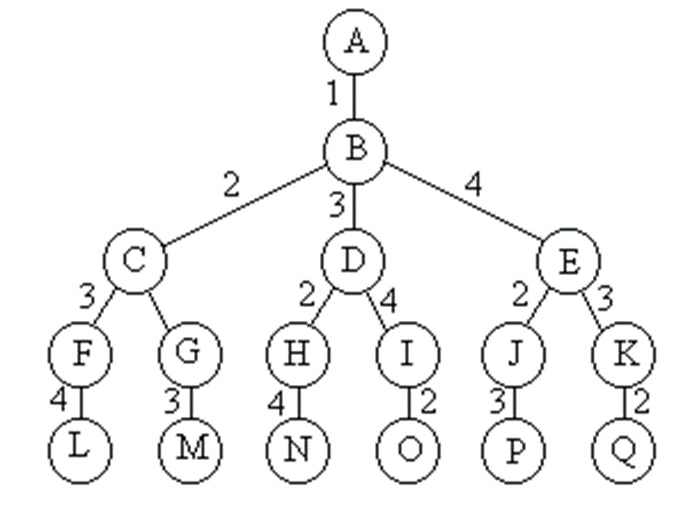
遍历排列树需要O(n!)计算时间 (就是有n!个叶子节点,n个元素的排列数就是n!)
1 | void backtrack (int t) |
装载问题

算法思想
有点类似于贪心,首先需要将第一艘传尽可能装满,然后剩下的箱子放第二艘船
而将第一艘船装满,就是一种0-1背包问题
解空间树是子集树
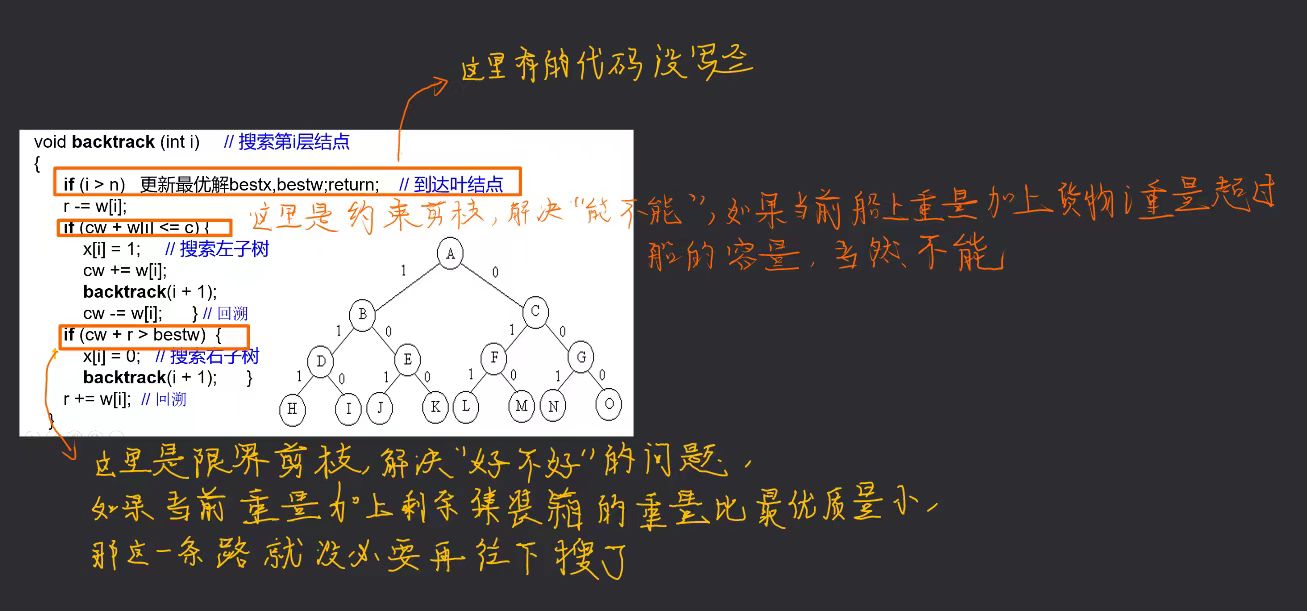
在上面两个剪枝下如果能遍历到叶子节点就是最优解
批处理作业调度

在机器1上是一条线,就是所有作业在机器1上耗时和
但是在机器2上就断断续续的,并且每一次机器2的结束就是一个任务的结束,将所有任务的结束时间相加就是要得到的完成时间
算法思想
解空间树是排列树
代码分析

n皇后
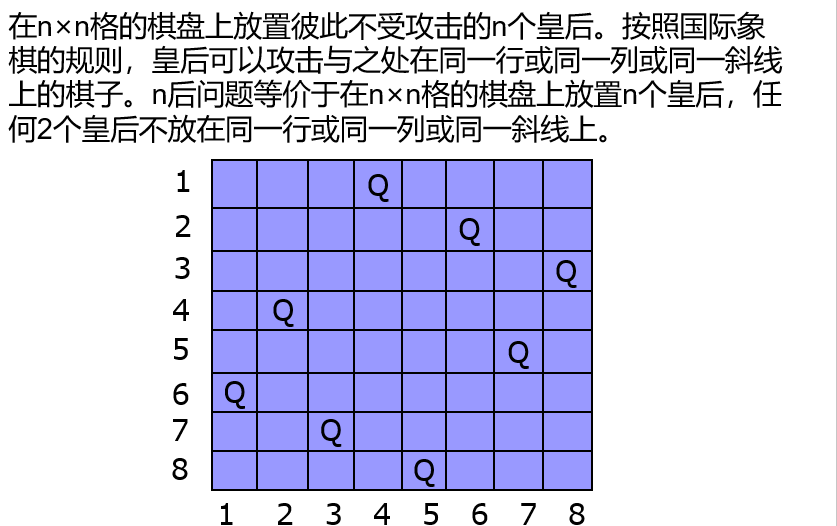
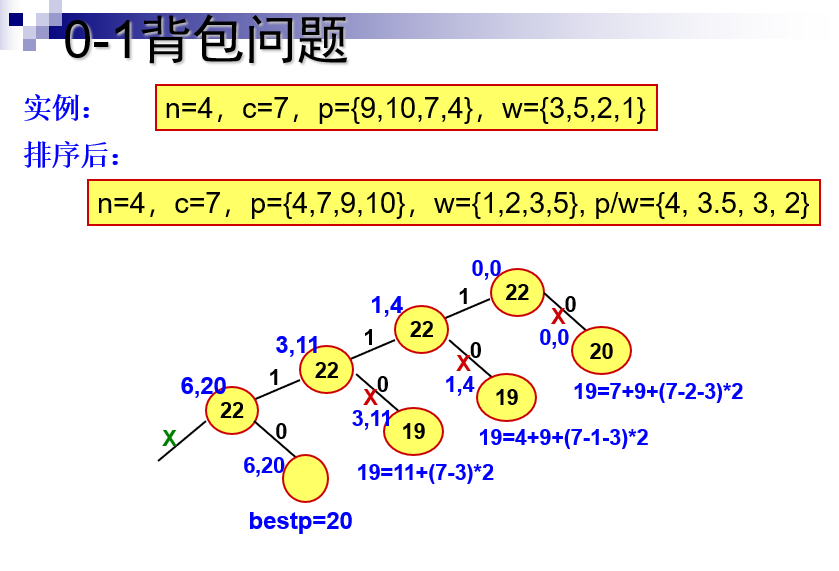
再探0-1背包
算法思想
一个子集树,每一层对应一个物品,左子树放这个物品(来),右子树不放这个物品(不来)
限界函数
- 将0-1背包看成背包,就是物品可以拆,利用贪心,先将所有物品按照单位价值排序,然后依次放入背包,剩下不能放下一整个物品的就拆开来放,这样就能得到当前状态节点往下走能获得的最大价值。
- 将这个最大价值与bestp比较判断有没有继续往下走的必要
- bestp是在走到叶子节点后才能得出
最大团
一些定义
完全子图和最大团
完全子图就是从一个图中抽出一部分顶点,这些顶点两两之间都有边相连
最大团就是一个图中顶点数最多的完全子图
举例:
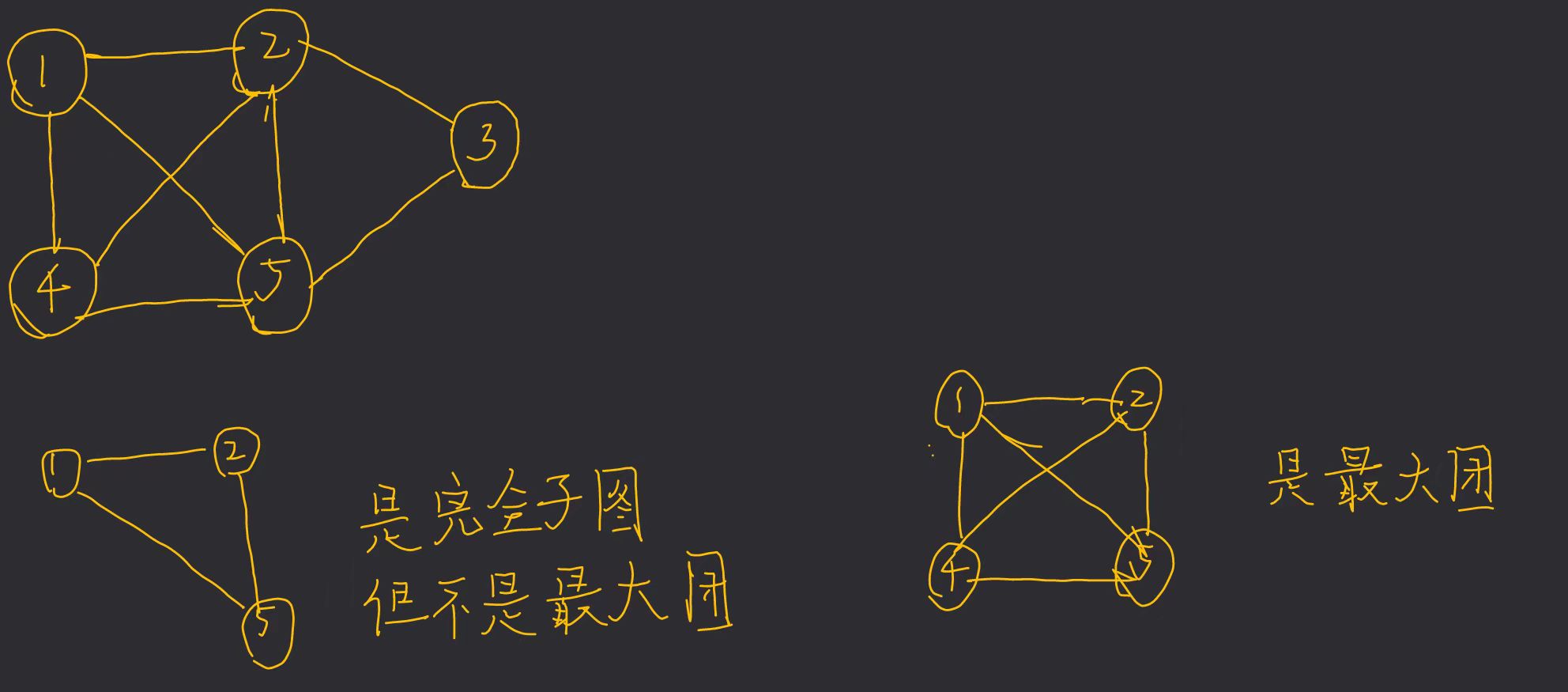
空子图和最大独立集
空子图和最大独立集就是上面的相对,节点两两之间没有边相连
算法思想
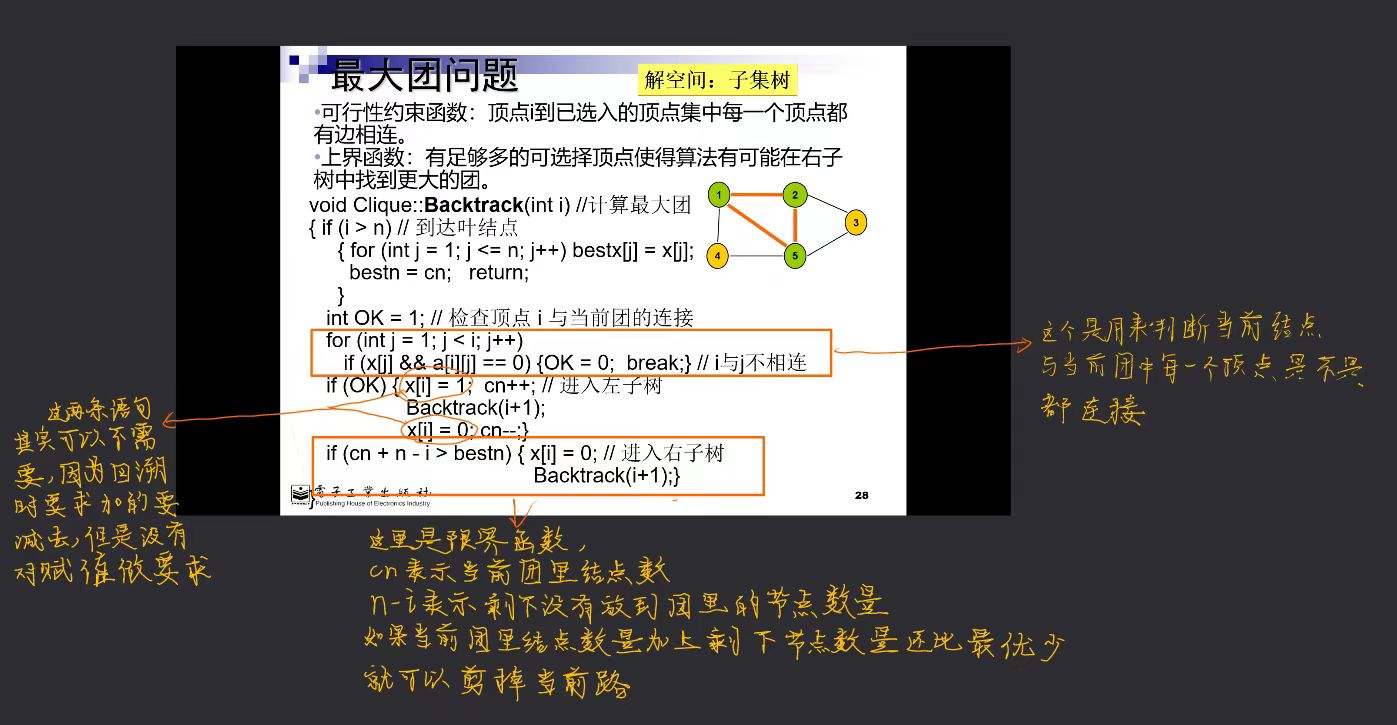
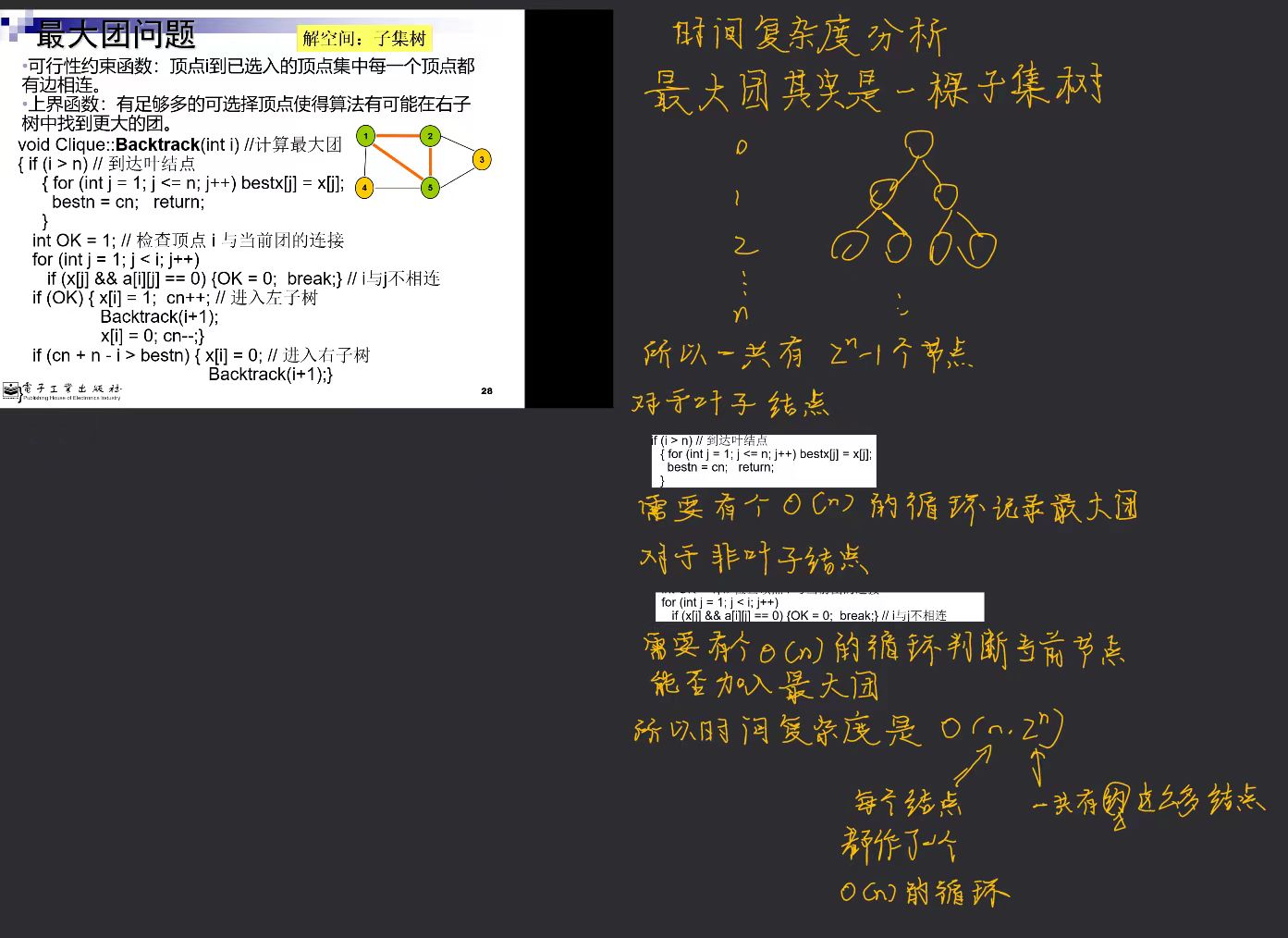
时间复杂度分析如下
图的m着色
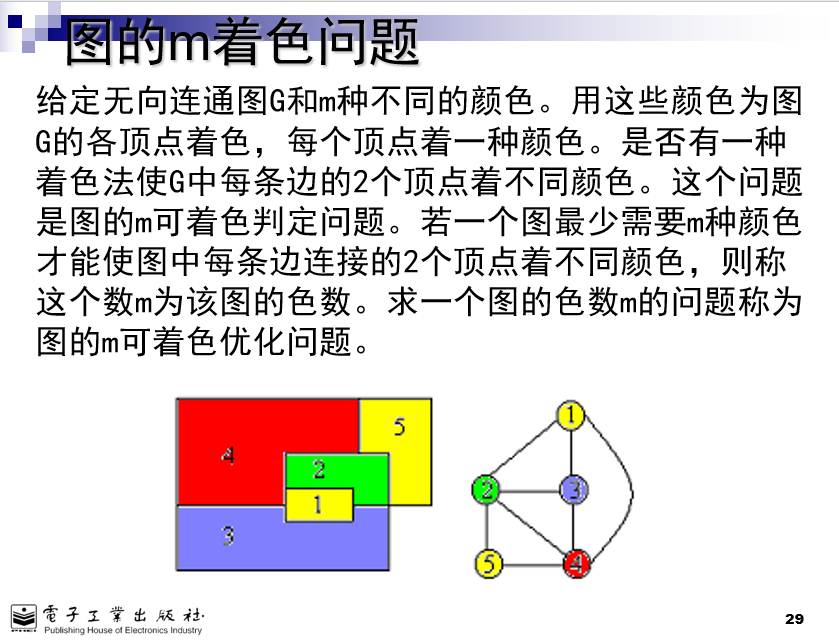
算法思想
•解向量:(x1, x2, … , xn)表示顶点i所着颜色x[i]
•可行性约束函数:顶点i与已着色的相邻顶点颜色不重复。
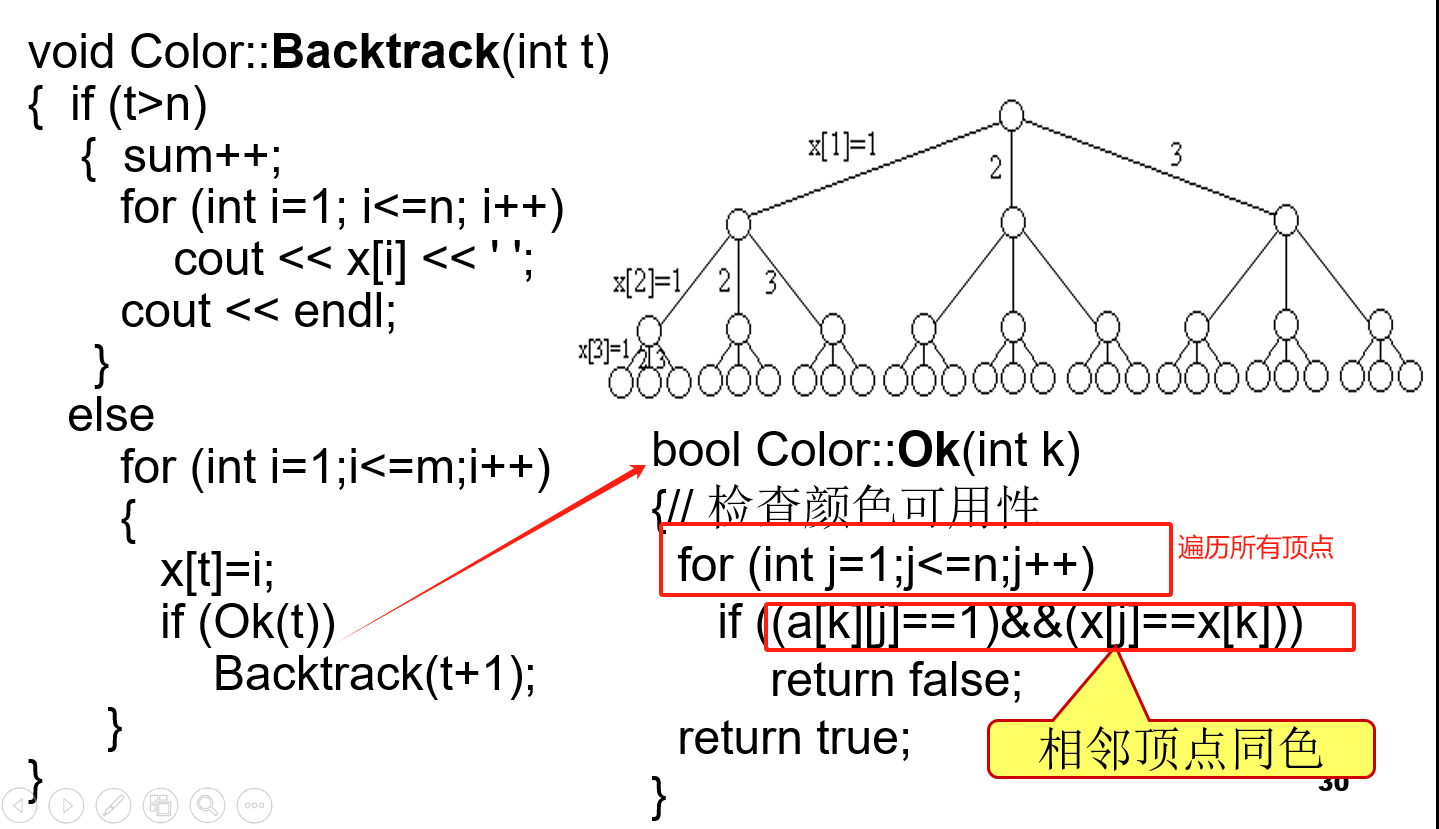
时间复杂度分析类似上面的最大团
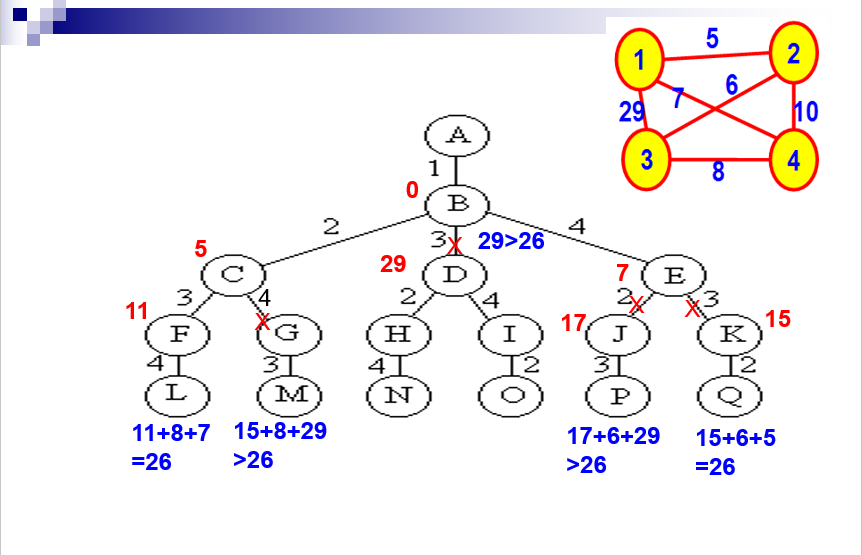
旅行售货员
一个售货员从起点节点绕一圈回来并且走的路程最短
算法思想
是一个排列树
符号三角形
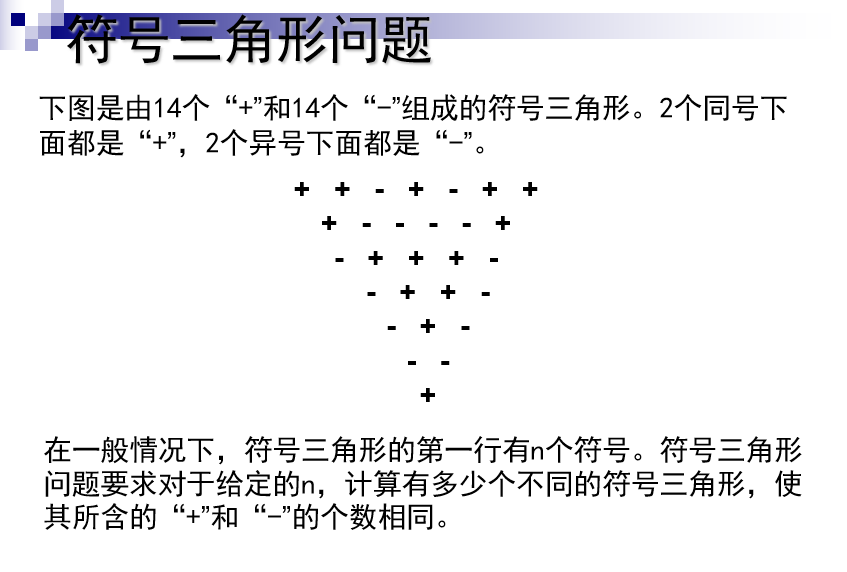
算法思想
- 解向量:用n元组x[1:n]表示符号三角形的第一行
- 可行性约束函数:当前符号三角形所包含的“+”个数与“-”个数均不超过n*(n+1)/4
- 无解的判断:n*(n+1)/2为奇数
- 比较反直觉的是,解空间是子集树不是排列树

概率方法估计回溯产生的节点数
