又探0-1背包
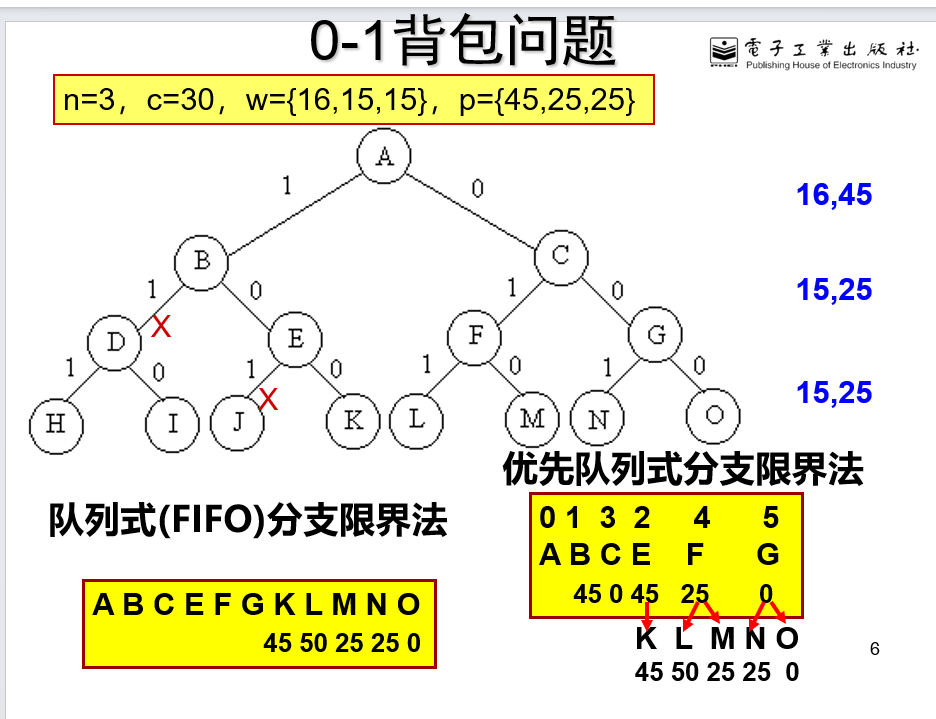
队列式分支限界法
就是按照普通队列先进先出规则,然后要注意可行性剪枝,升级可以加上限界剪枝
优先队列分支限界法
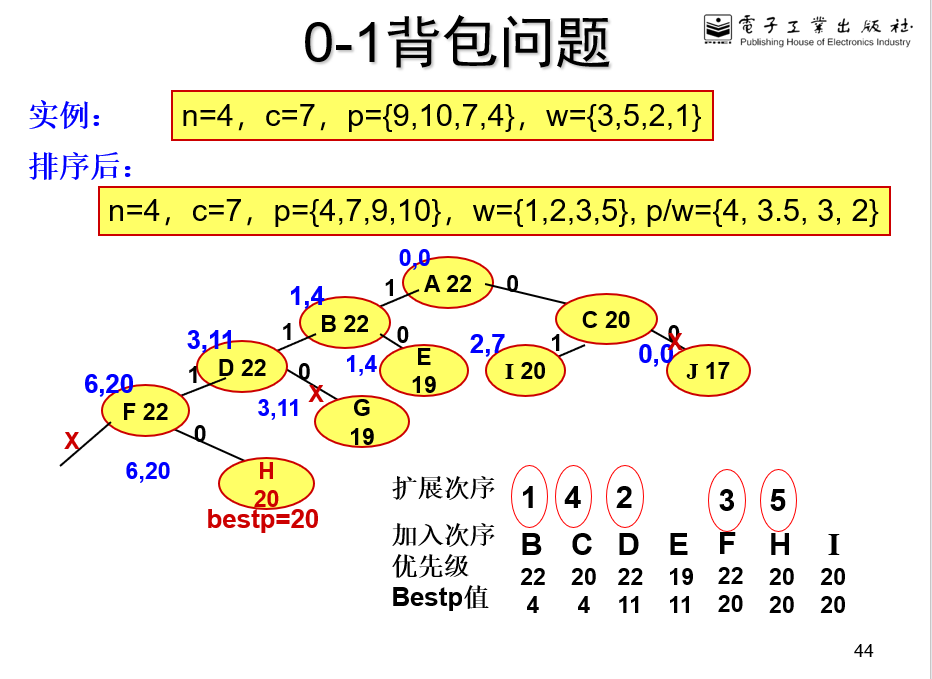
要选择一个优先的标准,本题标准就是当前背包里价值,优先将背包里价值大的出列并且将其对应的儿子放入队列中
广搜,根据优先级将当前节点出优先队列(一般是是大顶堆或者小顶堆),然后将当前节点的左孩子和右孩子加入优先队列,加入左孩子前要进行可行性剪枝,加入右孩子前进行限界剪枝
优先级:当前price最大的节点
限界函数:如果右节点贪心所得到的可能最大值比bestp小,就剪枝
注:这里的限界函数与深搜的做对比的,深搜是将右节点贪心所得到的可能最大值,就是深搜的bestp是在遍历到叶子才会产生,而广搜的bestp是可能没有遍历到叶子就得到了
又探旅行收货商
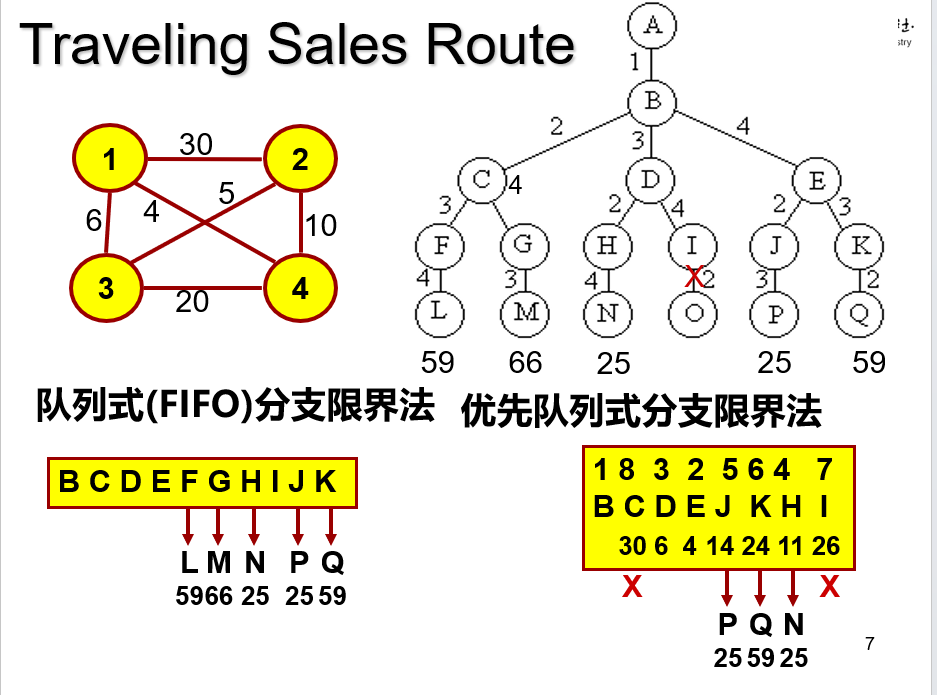
队列是分支限界法
优先队列分支限界法
- 优先级 = 当前已经走过的路程 + 未来走的最小路程
- 未来走的最小路程的计算方式:对于每个节点,计算从这个节点走出的最短路径,然后到达每个节点之后,要想计算未来走的最短路径,就是将从当前节点与所有还没有到过的节点的从这个节点走出的最短路径求和,所以建立的树的每一层的未来走的最小路程是相等的
- 其他注意点与优先队列一样,不懂可以看下面最大团里的视频讲解
单源最短路
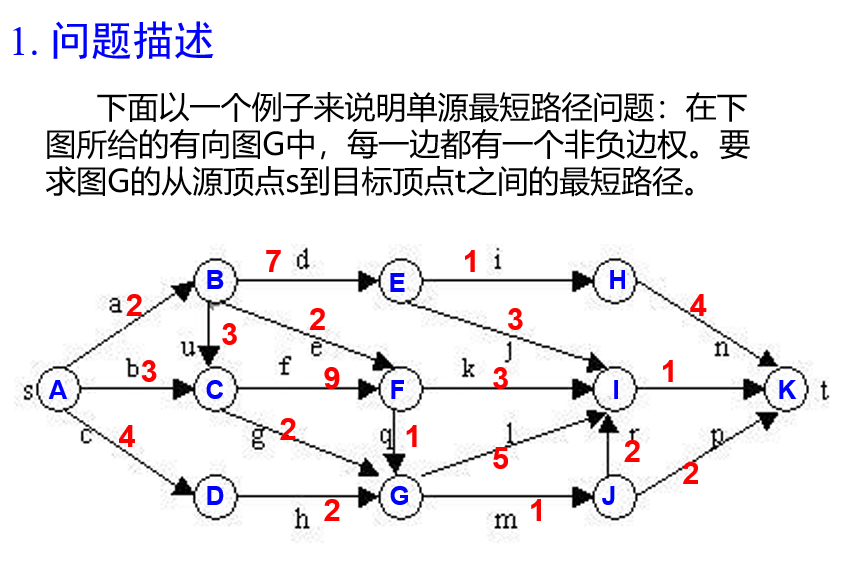
算法思想
就是迪杰斯特拉算法
这里的一种新型剪枝:如果优先队列中一个节点已经存在,又把这个节点放入优先队列,如果新放入的比原来的大,那么新放入的就被剪枝
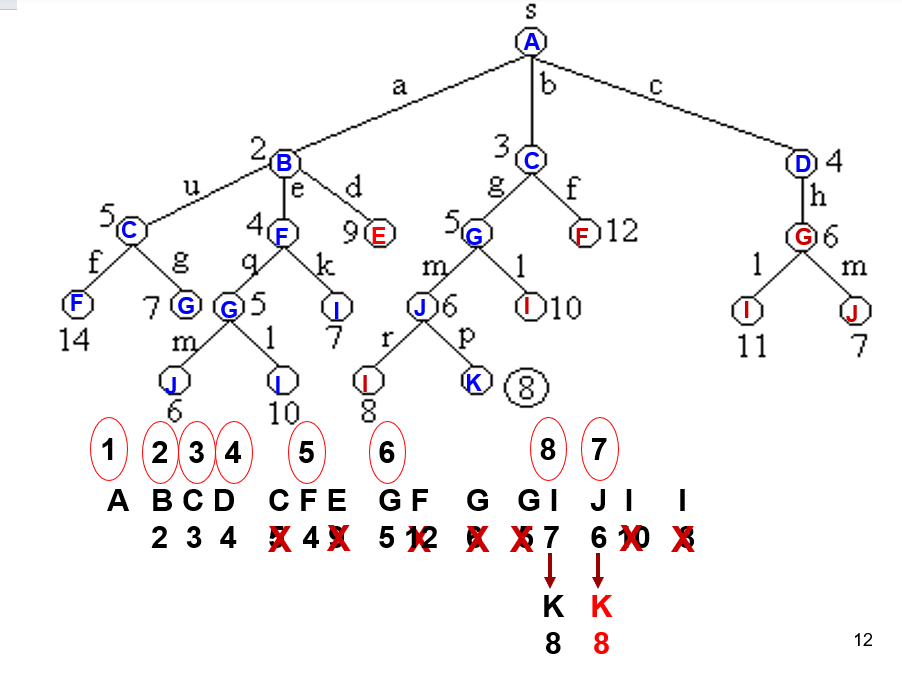

又探装载问题
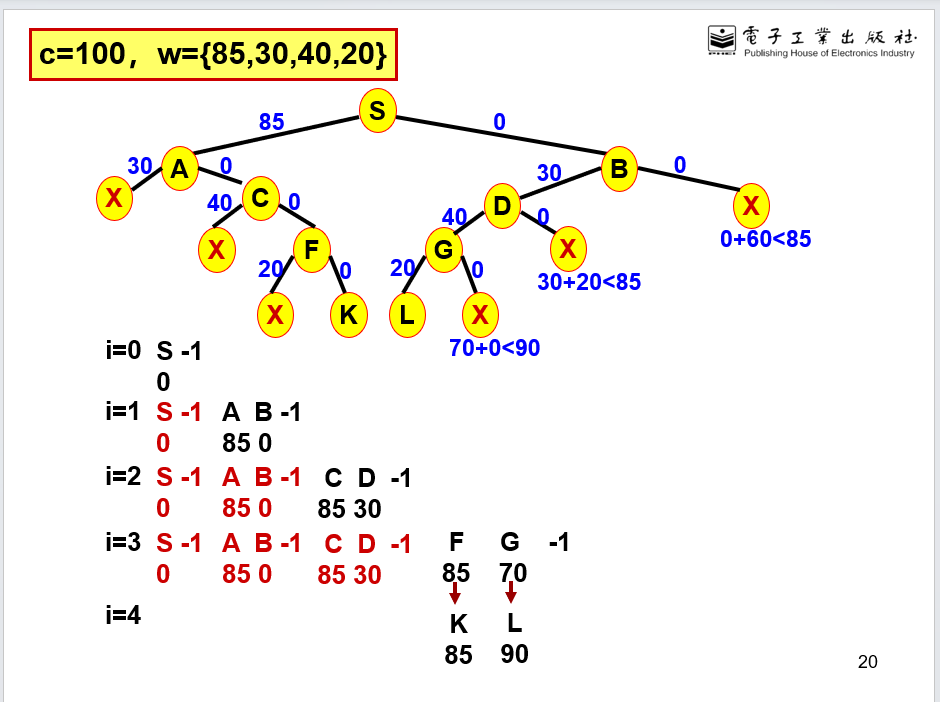
普通队列
普通队列并且加上了限界剪枝,限界剪枝函数是如果舍弃一个货物,判断当前船上货物加上剩余货物是否大于之前搜索得到的最大,如果小,这条路剪去
优先队列
又探最大团
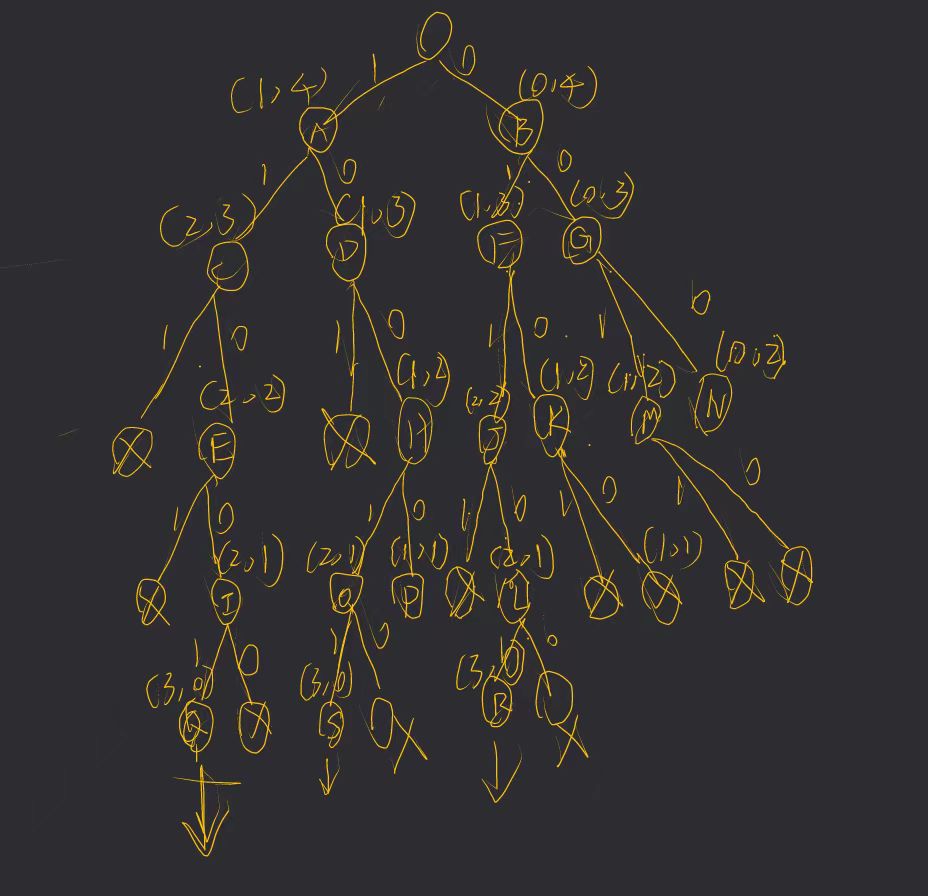
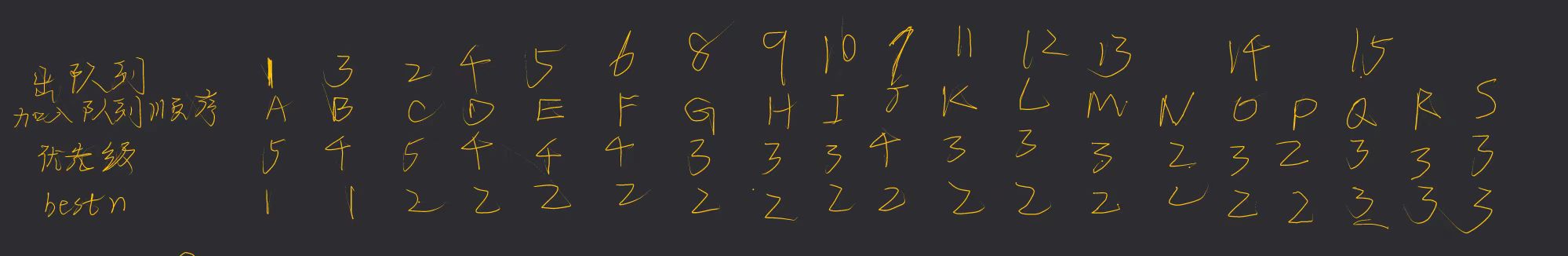
- 优先队列和树是同时画的
- 每次选择优先级最大的团
- 这里优先级的标准是(当前团里已有的元素) + (还没有遍历过的元素)
- 将优先级最大的出队,然后将它的孩子入队,左孩子要经过可行性剪枝才能入队,右孩子要经过限界剪枝才能入队
- 限界剪枝的标准是判断(当前团里已有的元素) + (还没有遍历过的元素)是否大于等于bestn,如果小就剪掉‘
- 如果优先级一样,就需要看优先队列里谁先入的队,先入队的先拓展
- 即使已经将最优节点找到了,也要继续往下遍历,直到当前遍历的节点就是叶子节点
布线问题
题目要求
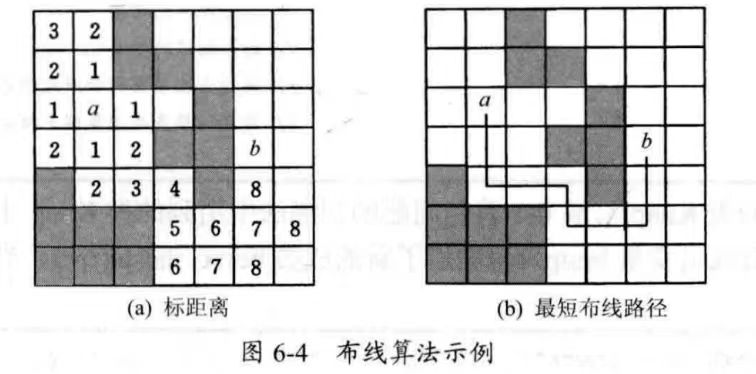
求从a到b的最短路线
算法思想
利用广搜,记录从起点到当前节点的路径长度,将当前节点加入队列
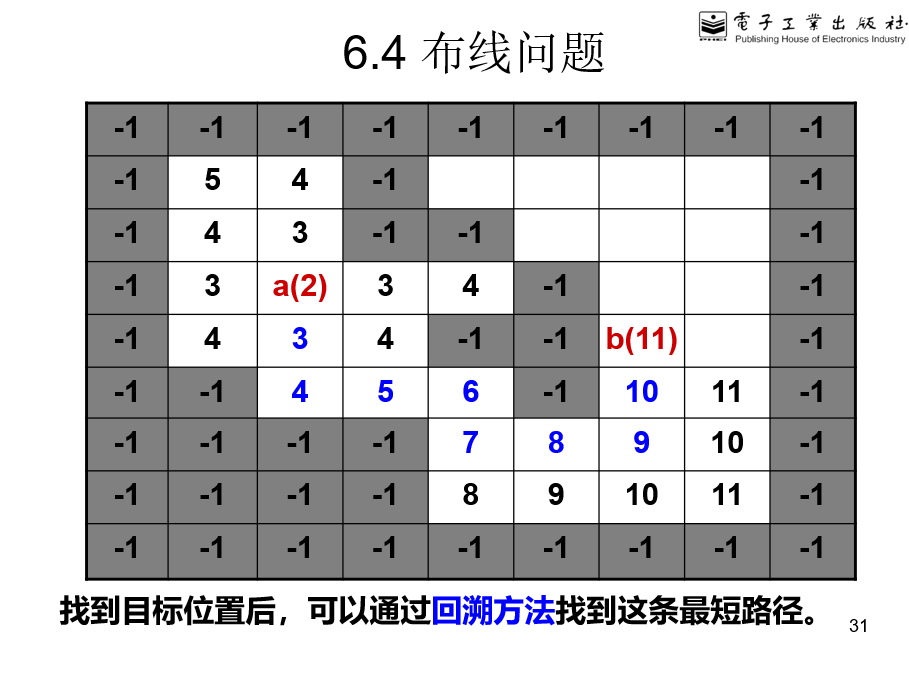
找到到终点的路径后,利用回溯,从终点往起点深搜,就是每次从当前节点出发搜一圈,如果有个节点路径长度减1就跳到这个节点,将这个节点加入堆栈直到找到起点,然后把堆栈里面所有倒出来就是要找的路径
代码


重排九宫问题
题目描述
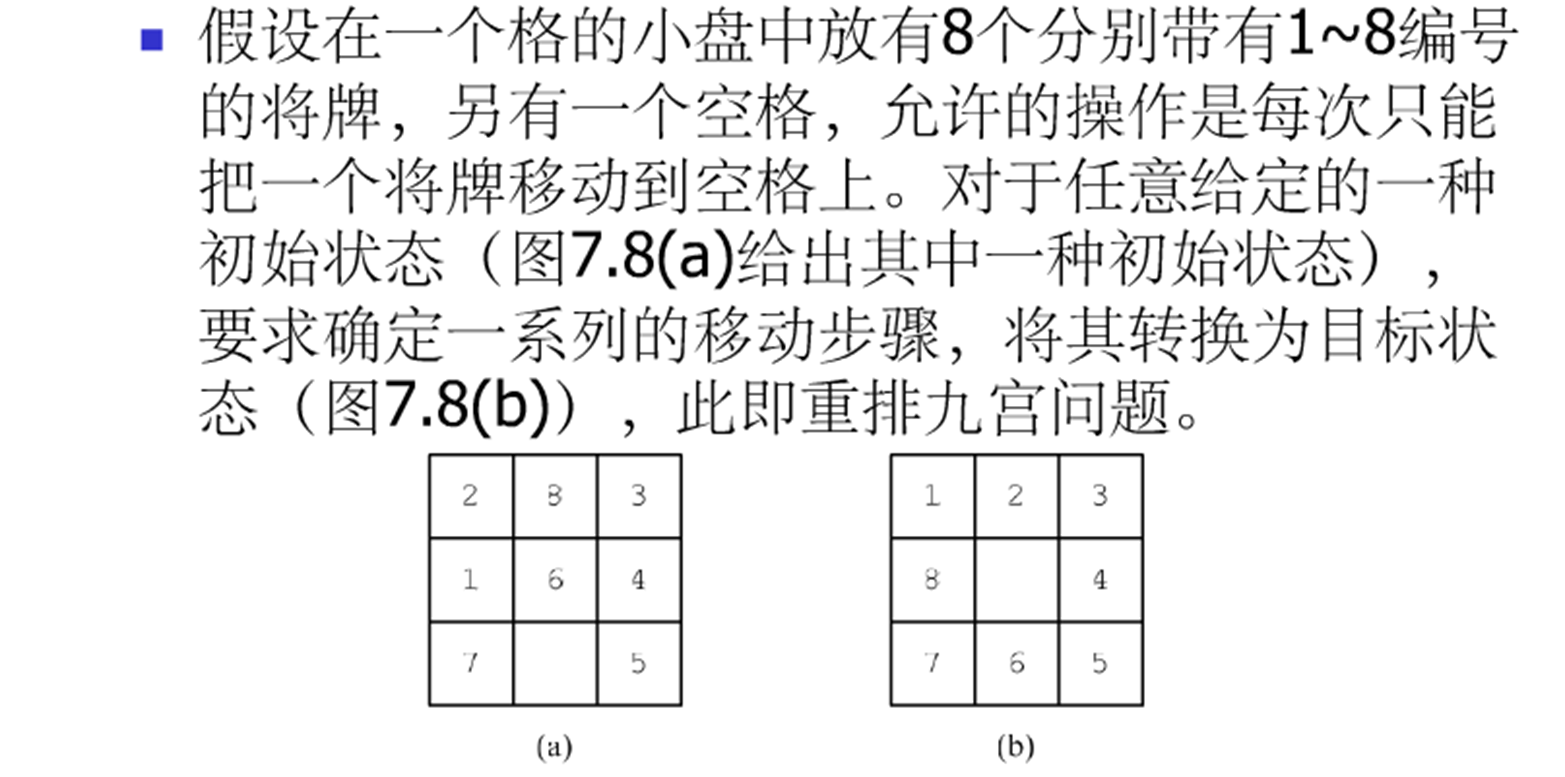
算法思想
优先级 = h(x)已移数字的次数(当前路径长) + p(x)错位数字离开目标位置距离之和 +s(x)每个数字与后接数字相对位置标记之和
s(x)= 0:x与后接数字相对位置不变 1:x在中心位置 2:其他
举例说明
第一个是目标状态,第二个是比较容易得到目标状态的状态,第三个是比较难得到目标状态的状态
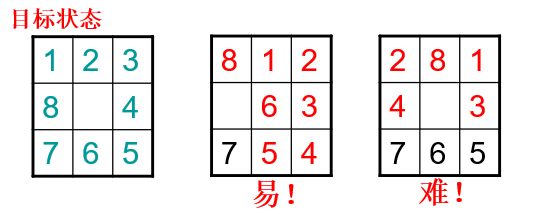
比较容易得到目标状态的状态的计算
P(1)=P(2)=…=P(6)=P(8)=1,P(7)=0
S(1)=S(2)=…=S(5)=S(8)=0,S(6)=1,S(7)=2
P(x)= 7, S(x)=3
P(x)+S(x)=10
比较难得到目标状态的状态的计算
P(1)=P(4)=P(8)=2, P(2)=P(3)=1,P(5)=P(6)=P(7)=0
S(5)=S(6)=S(8)=0, S(1)=S(2)=S(3)=S(4)=S(7)=2
P(x)= 9, S(x)=10
P(x)+S(x)=19