函数的定义与性质
定义
一句话,不能一对多
举例: 例 F1={<x1,y1>,<x2,y2>,<x3,y2>}
F2={<x1,y1>,<x1,y2>}
F1是函数, F2不是函数
注:如果两个函数相等,定义域和值域都要相等
从A到B的函数
说白了,就是一个定义域A,在这个定义域上构建一个函数,由此产生的值域在集合B内,就叫从A到B的函数
写作\(B^A\),读作B上A,A为定义域,B为值域
举例:
设A={1,2,3}, B={a,b}, 求\(B^A\)
f0 = {<1,a>,<2,a>,<3,a>}
f1 = {<1,a>,<2,a>,<3,b>}
f2 = {<1,a>,<2,b>,<3,a>}
f3 = {<1,a>,<2,b>,<3,b>}
f4 = {<1,b>,<2,a>,<3,a>}
f5 = {<1,b>,<2,a>,<3,b>}
f6 = {<1,b>,<2,b>,<3,a>}
f7 = {<1,b>,<2,b>,<3,b>}
函数的性质
设 f:A→B
满射
值域中每一个元素都在定义域中有对应元素,不过不一定是一个
单射
值域中一个元素如果被映射,那么在定义域中能映射到它的x只有一个
只要x不同,y就不同
双射
一一对应
注:双射函数一般都是单调函数
举例:
例2 判断下面函数是否为单射, 满射, 双射的, 为什么? (1) \(f:\mathbb{R} \to \mathbb{R}, f(x) = -x^2+2x-1\) (2) \(f:\mathbb{Z}^+ \to \mathbb{R}, f(x) = \ln x\), \(\mathbb{Z}^+\)为正整数集 (3) \(f:\mathbb{R} \to \mathbb{Z}, f(x) = \lfloor x \rfloor\) (4) \(f:\mathbb{R} \to \mathbb{R}, f(x) = 2x + 1\) (5) \(f:\mathbb{R}^+ \to \mathbb{R}^+, f(x) = \frac{x^2+1}{x}\), 其中 \(\mathbb{R}^+\) 为正实数集
判断:
重新打印上面段落,将不可见字符用人可以阅读的形式打印如下:
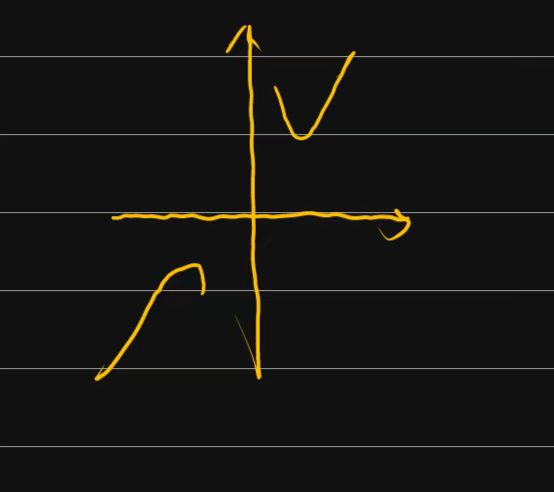
解 (1) \(f:\mathbb{R} \to \mathbb{R}, f(x) = -x^2 + 2x - 1\) 图像是抛物线,既不是单射也不是满射的。 (2) \(f:\mathbb{Z}^+ \to \mathbb{R}, f(x) = \ln x\) 是单调上升的,是单射的。但不满射, \(\text{ran} f = \{\ln 1, \ln 2, \ldots\}\)。 (3) \(f:\mathbb{R} \to \mathbb{Z}, f(x) = \lfloor x \rfloor\) 是满射的,但不是单射的,例如 \(f(1.5) = f(1.2) = 1\)。 (4) \(f:\mathbb{R} \to \mathbb{R}, f(x) = 2x + 1\) 是满射、单射、双射的,因为它是单调函数并且 \(\text{ran} f = \mathbb{R}\)。 (5) \(f:\mathbb{R}^+ \to \mathbb{R}^+, f(x) = \frac{x^2 + 1}{x}\) 有极小值 \(f(1) = 2\)。该函数既不是单射的也不是满射的。

单射定义域基数小于等于值域(因为只要x不同,y就不痛,那么值域至少和定义域相等,值域可以更大)
满射定义域基数大于等于值域(因为y都可以找到对应,那么定义域至少和值域相等或者更大)
双射的话定义域A和值域B的基数(就是集合中元素的数量)相等
恒等映射
自己到自己
函数的像与完全原像
像
给一个定义域集合,函数的像就是这个定义域集合对应的值域集合
注:函数像与函数值的区别在于像是一个集合,值是一个元素
完全原像
给一个值域中的数,得到定义域中一个集合,这个集合中所有数经过函数都可以得到这个值域中的值

某些重要函数
特征函数
在定义域里再划分一个小子集,在这个小子集里的都是1,不在里面的就是0

自然映射
举例:

函数的复合与反函数
函数的复合
定义
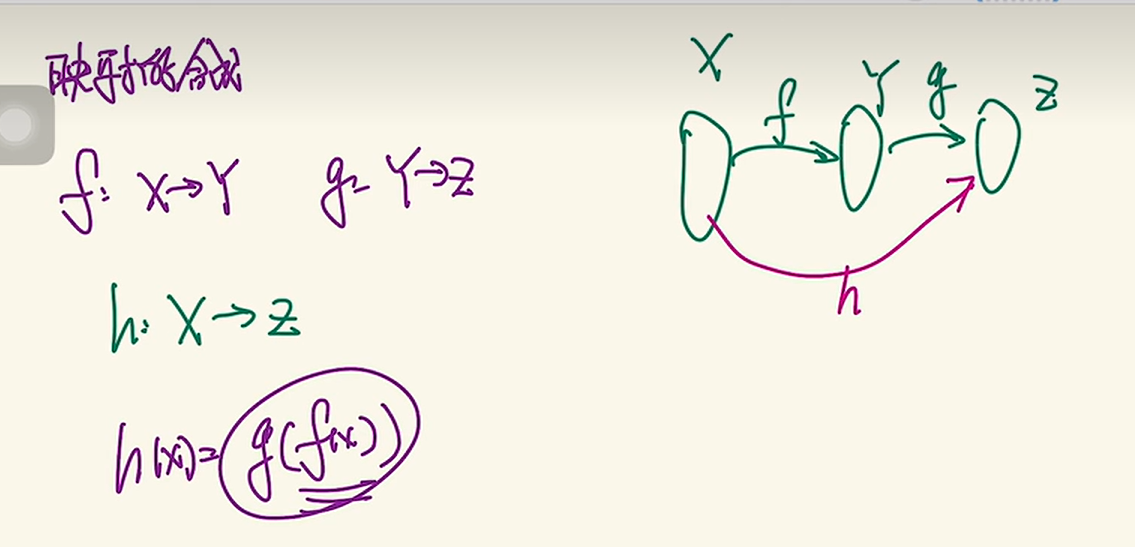
有顺序,所以不满足交换律,满足结合律

上图说明的就是从X到最终结果W有不同的路径,左图路径是X -> Z -> W,右图路径是X -> Y -> W
关于单射满射和双射的定理
定理8.2 设 \(f:A \to B\), \(g:B \to C\) (1) 如果 \(f:A \to B\), \(g:B \to C\) 是满射的, 则 \(f \circ g:A \to C\) 也是满射的 (2) 如果 \(f:A \to B\), \(g:B \to C\) 是单射的, 则 \(f \circ g:A \to C\) 也是单射的 (3) 如果 \(f:A \to B\), \(g:B \to C\) 是双射的, 则 \(f \circ g:A \to C\) 也是双射的
反函数

原像与逆映射的区别,下面就是一个反例
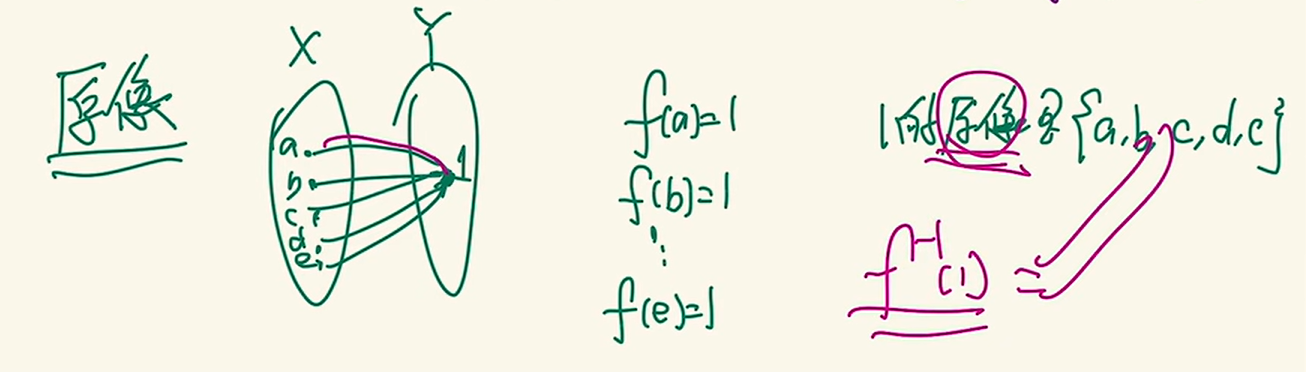
充要条件是一一映射,也就是双射
双射函数与集合的基数
势
势的定义
设A, B是集合, 如果存在着从A到B的双射函数, 就称A和B是等势的, 记作A≈B. 如果A不与B 等势, 则记作A≉B.
势的性质
定理8.6 设A, B,C是任意集合, (1) A≈A ("自反") (2) 若A≈B,则B≈A ("对称") (3) 若A≈B,B≈C,则A≈C. ("传递")
集合的优势
从A到B的单射函数就叫B优势于A,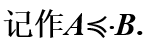
等势与不等势
等势
- N ≈ Z ≈ Q ≈ N×N
- 任何实数区间都与实数集合R等势
不等势

集合基数
就是集合中元素的数量
常见集合的基数
对于有穷集合 \(A\),称与 \(A\) 等势的那个惟一的自然数为 \(A\) 的基数,记作 \(\text{card}(A)\)(也可以记作 \(|A|\)) \(\text{card}(A) = n \iff A \approx n\)
自然数集合 \(\mathbb{N}\) 的基数记作 \(\aleph_0\),即 \(\text{card}(\mathbb{N}) = \aleph_0\)
实数集 \(\mathbb{R}\) 的基数记作 \(\aleph\),即 \(\text{card}(\mathbb{R}) = \aleph\)
基数和势的关系
定义8.13 设 \(A\), \(B\) 为集合, 则 (1) \(\text{card}(A) = \text{card}(B) \iff A \approx B\) (2) \(\text{card}(A) \leq \text{card}(B) \iff A \preceq . B\) (3) \(\text{card}(A) < \text{card}(B) \iff \text{card}(A) \leq \text{card}(B) \wedge \text{card}(A) \neq \text{card}(B)\)
基数的大小
不存在最大的基数。将已知的基数按从小到大的顺序排列就得到: 0, 1, 2, …, n, …, \(\aleph_0\), \(\aleph\), …
其中: 0, 1, 2, …, n, … 是全体自然数,是有穷基数。 \(\aleph_0\), \(\aleph\), … 是无穷基数,\(\aleph_0\) 是最小的无穷基数,\(\aleph\) 后面还有更大的基数,如 \(\text{card}(\mathcal{P}(\mathbb{R}))\) 等。