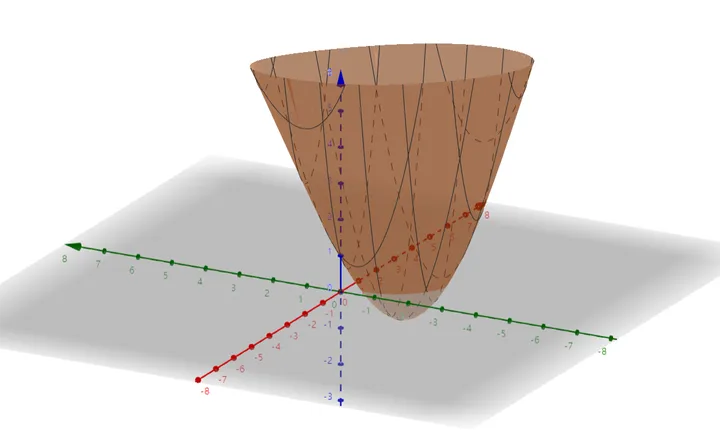
求一元单峰函数的极值

二分法使用的场景是单调函数，也就是一次函数。

三分法会将区间分成三份，这个我们都已经知道了。分成三份，自然需要两个端点。这两个端点各有一个值，我们分别叫做m1和m2。我们要求的是函数的最小值，所以我们要想极值逼近。

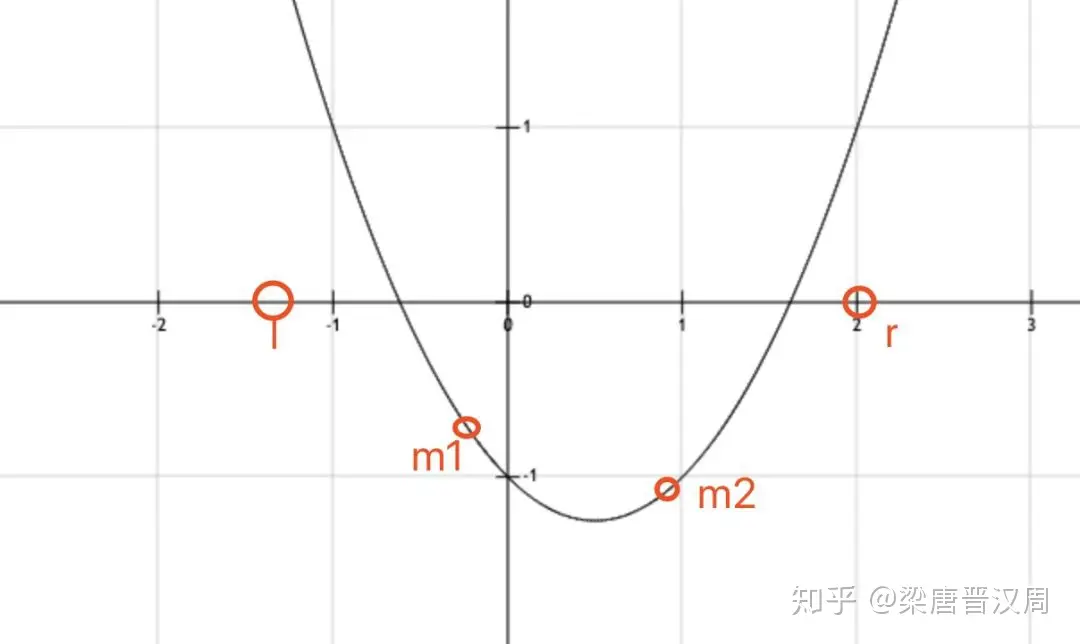
每次通过比较两个值的大小，缩小三分之一的区间。直到最后区间的范围小于我们设定的阈值为止

三分法是二分法的变种，他最基本的用途是求单峰函数的极值点。

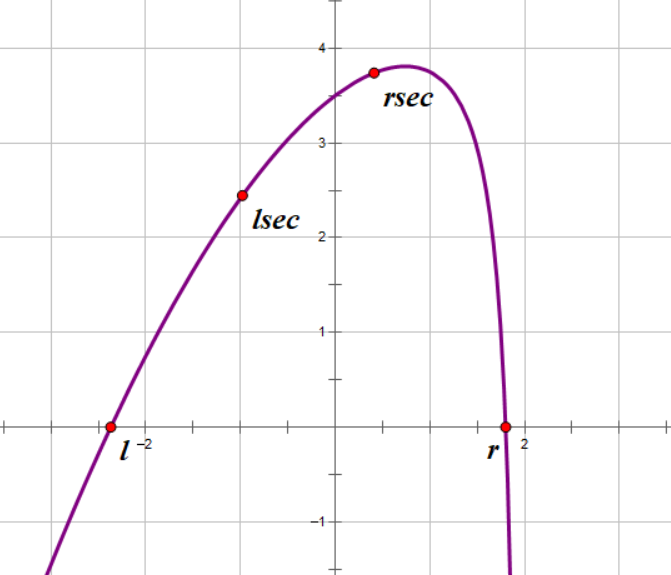
以求极大值为例，每次对一个区间[l,r]求三等分点lsec和rsec：

如果f(lsec) < f(rsec) ，说明极大值一定在[lsec,r]内取到，因为如果在[0,lsec)内，那rsec一定处于单调下降的区间内，它的函数值不可能大于lsec的函数值。于是我们令l=lsec并继续。

如果f(lsec) > f(rsec)，同理，极大值一定在[l,rsec]内取到，令r=rsec并继续。

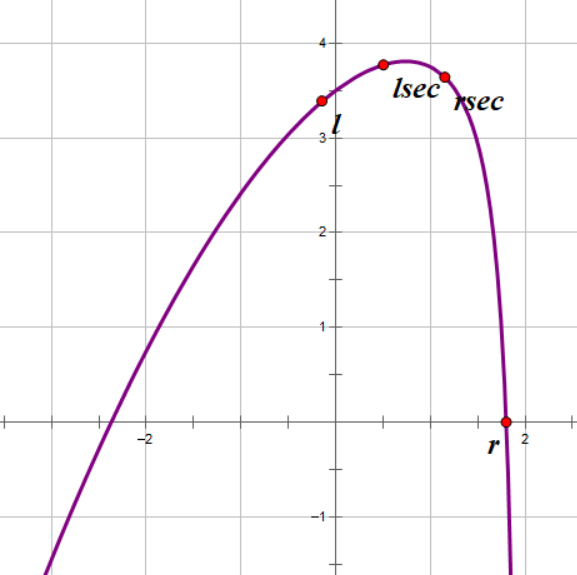
这样进行下去，直到l和r的差距小于设定的eps为止。如果求的是极小值而非极大值，只需把上面条件判断处的大于、小于互换。

求二元函数的极致

三分套三分