题目

从 1∼n 这个整数中随机选取任意多个，输出所有可能的选择方案。

输入格式

输入一个整数 n。

输出格式

每行输出一种方案。

同一行内的数必须升序排列，相邻两个数用恰好 11 个空格隔开。

对于没有选任何数的方案，输出空行。

本题有自定义校验器（SPJ），各行（不同方案）之间的顺序任意。

数据范围

1≤n≤15

输入样例：

输出样例：

分析

利用dfs的思想递归，每一层对应当前的数，分成两个子树，左子树代表选，右子树代表不选

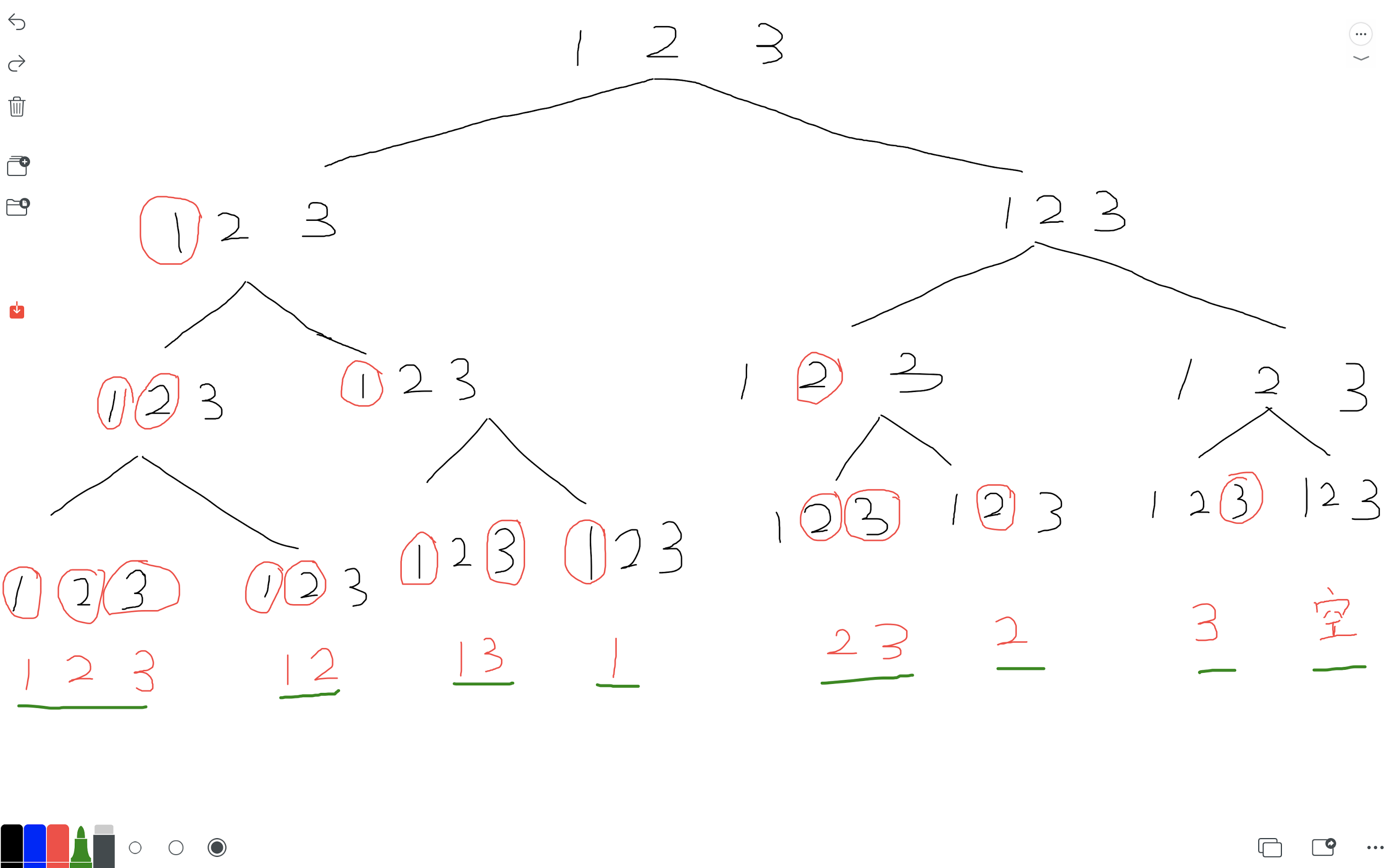
代码

import java.util.Scanner;
public class Main {
	static int n;
	static boolean[] isChoose = new boolean[16];
	static void dfs(int a) {
		if(a > n) {	//如果当前层超过最后一层，就可以输出全部结果了
			for(int i = 1; i <= n; i++) {
				if(isChoose[i]) {
					System.out.print(i + " ");
				}
			}
			System.out.println();
		} else {	//如果还没有超过最后一层
			// 选当前层
			isChoose[a] = true;
			dfs(a + 1);
			// 不选当前层
			isChoose[a] = false;
			dfs(a + 1);
		}
	}
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		n = scan.nextInt();
		dfs(1);
		scan.close();
	}
}

举一反三

题目一

递归三要素：参数值和返回值，终止条件，递归逻辑

root表示当前的根，count表示当前root对应是第几层

题目二

分析

为什么要把这题放在枚举里面了？

因为这是就是一道用dfs解决的题目

因为一共有16个开关，每个开关有2种选择，所以一共有\(2^{16}\)种选择，所以可以用暴力解决

用dfs树的思路：当前层的开关不调整是左子树，调整是右子树，如果是右子树就要将该开关本身所在的行与列都调整

举个例子

代码

import java.util.Arrays;
import java.util.Scanner;
public class Main {
    static char CLOSED = '-';
    static char OPEN = '+';
    static char[][] data = new char[4][4];
    static boolean[][] tmpIsVisited = new boolean[4][4];
    static boolean[][] minIsVisited = new boolean[4][4];
    static int minStride = Integer.MAX_VALUE;
    static int tmpStride = 0;
    static boolean validate() {
        boolean flag = true;
        for(int i = 0; i < 4; i++) {
            for(int j = 0; j < 4; j++) {
                if(data[i][j] == OPEN) {
                    flag = false;
                    break;
                }
            }
        }
        return flag;
    }
    static void reverse(int row, int col) {
        if(data[row][col] == CLOSED) {
            data[row][col] = OPEN;
        } else {
            data[row][col] = CLOSED;
        }
    }
    static void change(int row, int col) {
        reverse(row, col);
        for(int i = 0; i < 4; i++) reverse(row, i);
        for(int j = 0; j < 4; j++) reverse(j, col);
    }
    static void dfs(int count) {
        if(count == 16) {
            if(validate()) {
//              printMatrix();
                if(tmpStride < minStride) {
                    minStride = tmpStride;
                    for(int i = 0; i < 4; i++) {
                        minIsVisited[i] = Arrays.copyOf(tmpIsVisited[i], 4);
                    }
                }
            }
            return;
        }
        int row = count / 4;
        int col = count % 4;
//      System.out.format("当前开关是%d %d\n", row, col);
//      System.out.println("当前层开关不按");
//      printMatrix();
        dfs(count + 1);
        tmpIsVisited[row][col] = true;
        change(row, col);
//      System.out.println("当前层开关按");
//      printMatrix();
        tmpStride += 1;
        dfs(count + 1);
        tmpIsVisited[row][col] = false;
        change(row, col);
        tmpStride -= 1;
//      System.out.println("恢复当前层");
//      printMatrix();
    }
    static void printMatrix() {
        for(int i = 0; i < 4; i++) {
            for(int j = 0; j < 4; j++) {
                System.out.print(data[i][j] + " ");
            }
            System.out.println();
        }
        System.out.println("----------------------");
    }
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        // 读取
        int row = 0;
        while(scan.hasNextLine() && row < 4) {
            String line = scan.nextLine();
            for(int i = 0; i < 4; i++) {
                data[row][i] = line.charAt(i); 
            }
            row++;              
        }
        dfs(1);
        change(0, 0);
        tmpStride += 1;
        tmpIsVisited[0][0] = true;
        dfs(1);
        
        System.out.println(minStride);
        for(int i = 0; i < 4; i++) {
            for(int j = 0; j < 4; j++) {
                if(minIsVisited[i][j] == true) {
                    System.out.format("%d %d\n", i + 1, j + 1);
                }
            }
        }
        scan.close();
    }
 }

Pilot's Blog

递归实现指数型枚举

题目