滤波
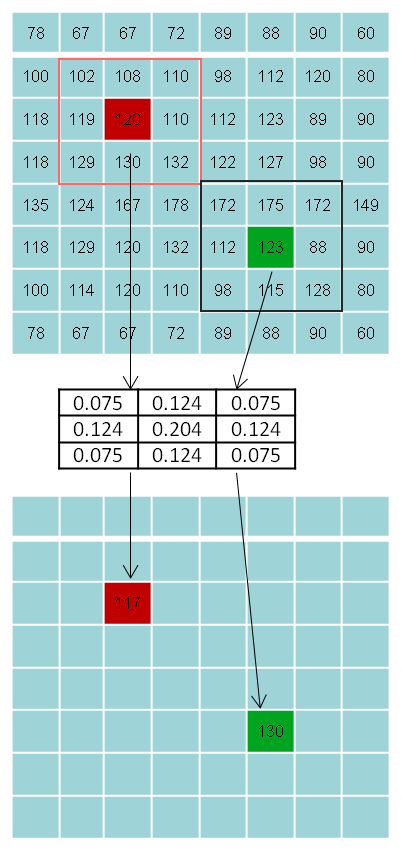
1 滤波是对输入信号进行卷积处理的一个过程,分两步 1.1 计算掩膜
1.2 将计算出的掩膜与原图卷积——掩膜上每一个位置的值和图像上对应位置的像素值的乘加运算
2 卷积模板/掩膜 的不同决定了不同的滤波方式,也因此产生了高通、低通、带通、带阻等基本的滤波方式。
低通滤波,就是保留将信号中的低频部分,抑制高频部分。要达到这个目的,可以利用均值掩膜、高斯掩膜等对输入信号进行处理。 采用均值掩膜对输入信号进行卷积的滤波方式叫均值滤波; 采用高斯掩膜对输入信号进行卷积的滤波方式叫高斯滤波;
举个例子:均值掩膜
3x3均值滤波的掩膜:
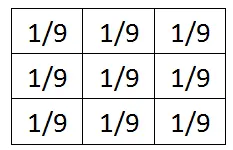
均值掩膜内所有系数均相等——为1/9,且他们的和为1
高斯滤波(高斯滤波和高斯模糊指的是一个操作)
高斯分布
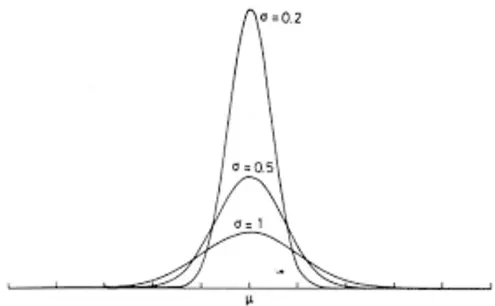
正态分布,\(\mu\)决定了分布对称中心,\(\sigma\)决定了分布的形状——越小形状越瘦高,越大越矮胖
作用:计算高斯滤波用的掩膜(Mask)
如何利用高斯分布求掩膜
高斯分布公式是一维的,但掩膜是二维的怎么办? 很简单,只需要把数值\(x\)变为向量\(\vec{x}\)即可:
\(\vec{x}\)表示一个点的坐标
\(\vec{u}\)表示这个mask中心的坐标
举例说明
对于图像中任意一点(x,y),它周围的坐标为:
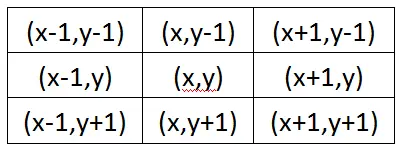
遍历所有点与均值做差后平方
中间的(x,y)就是\(\vec{u}\)了, 当\(\vec{x}\)遍历图中所有点时,计算\((\vec{x}-\vec{u})^2\),其中x和y被消除,得到下面
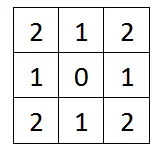
带入正态分布公式
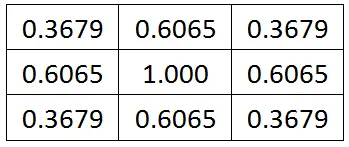
归一化
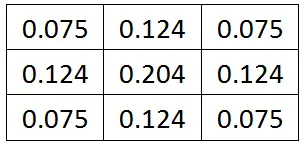
利用高斯掩膜和图像进行卷积求解高斯模糊
如下图所示,没有别的,就是卷积