有序对与笛卡儿积
有序对
定义
由两个元素 x 和 y,按照一定的顺序组成的二元组称为有序对或序偶,记作<x,y>
性质
- 有序性\(<x,y> \neq
<y,x>\)(当\(x \neq
y\)时)
(2)\(<x,y>\)与\(<u,v>\)相等的充分必要条件是
\(<x,y> = <u,v> \iff x=u \land y=v\).
笛卡尔积
定义
设\(A,B\)为集合,\(A\)与\(B\)的笛卡尔积记作\(A \times B\),且\(A \times B = \{ <x,y> | x \in A \land y \in B \}\)
上面要求集合A中元素在前,集合B中元素在后
举例:
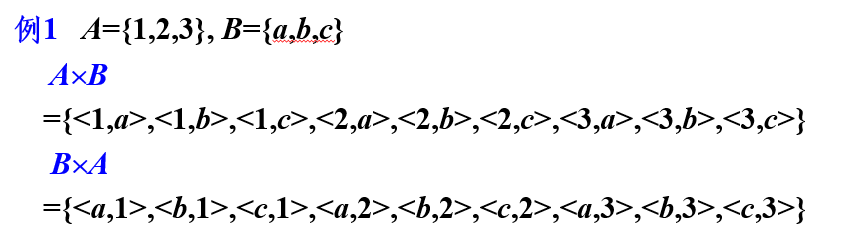
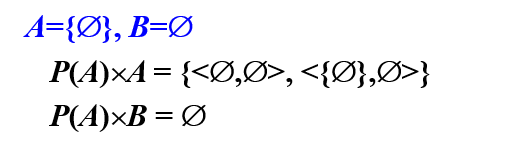
性质
不适合交换律: \(A \times B \neq B \times A \quad (\text{当 } A \neq B, A \neq \emptyset, B \neq \emptyset \text{ 时})\)
不适合结合律: \((A \times B) \times C \neq A \times (B \times C) \quad (\text{当 } A \neq \emptyset, B \neq \emptyset, C \neq \emptyset \text{ 时})\)
对于并或交运算满足分配律: \(\begin{align*} A \times (B \cup C) &= (A \times B) \cup (A \times C) \\ (B \cup C) \times A &= (B \times A) \cup (C \times A) \\ \\ A \times (B \cap C) &= (A \times B) \cap (A \times C) \\ (B \cap C) \times A &= (B \times A) \cap (C \times A) \end{align*}\)
若\(A\)或\(B\)中有一个为空集,则\(A \times B\)就是空集: \(A \times \emptyset = \emptyset \times B = \emptyset\)
若\(A \subseteq C\)且\(B \subseteq D\),则\(A \times B \subseteq C \times D\).
若\(|A| = m\),\(|B| = n\),则\(|A \times B| = mn\)
举例:
例1


二元关系
二元关系定义
如果一个集合满足以下条件之一:
集合非空, 且它的元素都是有序对
集合是空集
则称该集合为一个二元关系, 简称为关系,记作R
举例:

A到B的关系与A上的关系
定义
设A,B为集合, A×B的任何子集所定义的二元关系叫做从A 到B的二元关系, 当A=B时则叫做A上的二元关系.
举例:

注:关系数量的计算
A上的二元关系数量等价于A\(\times\)A的子集数量
举例:
A上重要关系
空关系
\(\emptyset\)是\(A\)上的关系,称为空关系。
全域关系
全域关系\(E_A = \{ (x,y) \mid x \in A \land y \in A \} = A \times A\)
恒等关系
恒等关系\(I_A = \{ (x,x) \mid x \in A \}\)
小于等于关系
小于等于关系\(L_A = \{ (x,y) \mid x,y \in A \land x \leq y \}\),\(A\)为实数子集
整除关系
整除关系\(D_A = \{ (x,y) \mid x,y \in A \land x \text{ 整除 } y \}\),\(A\)为非零整数子集
包含关系
包含关系\(R \subseteq = \{ (x,y) \mid x,y \in A \land x \subseteq y \}\),\(A\)是集合族。
举例:

关系的表示
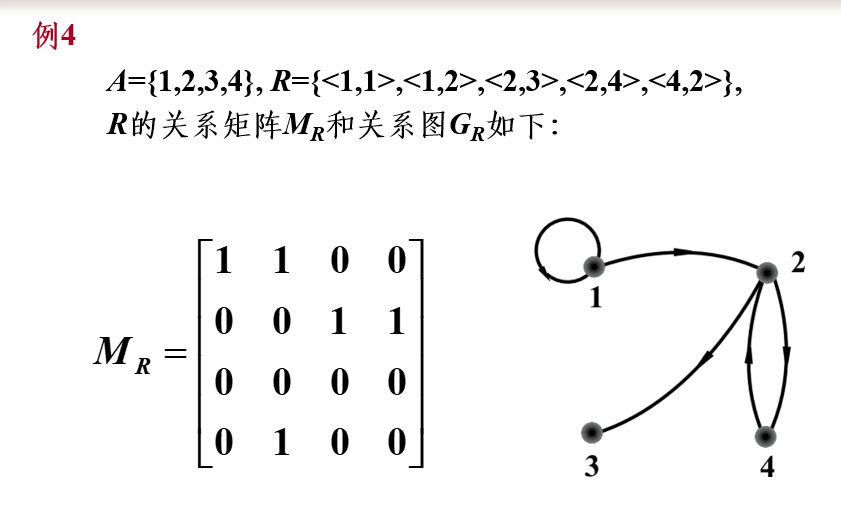
关系矩阵与关系图
举例:
关系的运算
定义域、值域与域
定义域:第一个元素组成的集合
值域:第二个元素组成的集合
域就是定义域和值域合并
举例:
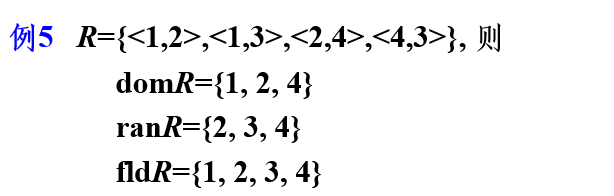
逆运算
就是前后交换位置
右复合运算\(\circ\)
两个不同关系集合之间某两个关系之间传递
举例:
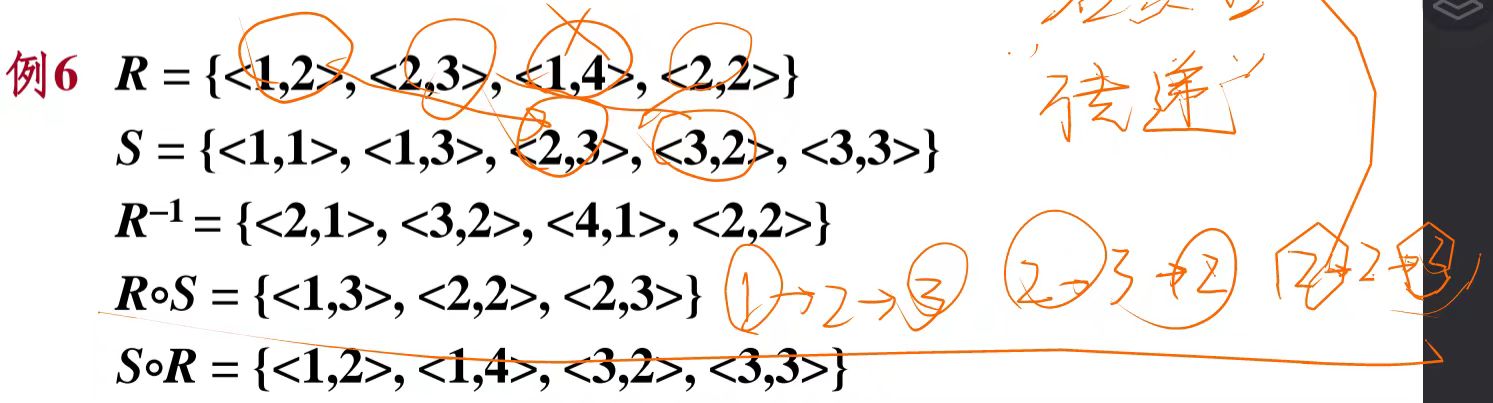
右复合(合成)画图
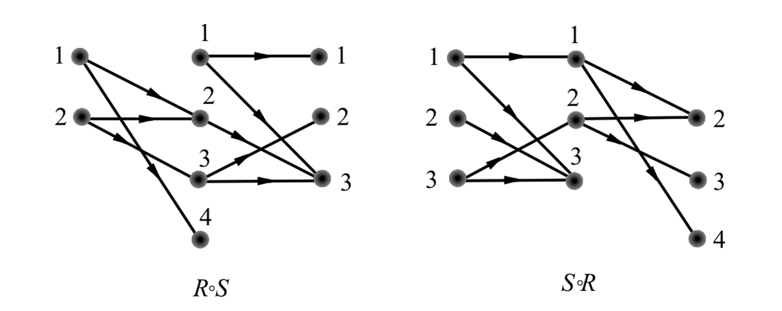
限制
依次从A中选择元素,这些元素作为关系集合R中第一位,获得的是一个有序对
R在A上的限制记作 R↾A, 其中 R↾A = { <x,y> | xRy∧x∈A }
像
依次从A中选择元素,这些元素在关系集合R中对应的第一位,获得的是一个元素
举例:
关系运算的性质
逆关系
"奇变偶不变",两重含义,一个是这个关系本身与自己的逆,一个是定义域与值域之间的转换
设\(F\)是任意的关系,则
\((F^{-1})^{-1} = F\)
\(\text{dom}(F^{-1}) = \text{ran}(F)\),\(\text{ran}(F^{-1}) = \text{dom}(F)\)
结合律
\((F \circ G) \circ H = F \circ (G \circ H)\)
逆关系的分配律
分配以后还要调换顺序
\((F \circ G)^{-1} = G^{-1} \circ F^{-1}\)
单位元
\(R \circ I_A = I_A \circ R = R\)
与并运算的分配律
\(F \circ (G \cup H) = F \circ G \cup F \circ H\)
\((G \cup H) \circ F = G \circ F \cup H \circ F\)
与交运算的分配包含
\(F \circ (G \cap H) \subseteq F \circ G \cap F \circ H\)
\((G \cap H) \circ F \subseteq G \circ F \cap H \circ F\)
限制↾与交、并的分配律
F ↾(A∪B) = F ↾A∪F ↾B
F ↾(A∩B) = F ↾A∩F ↾B
像[]与并分配,与交包含
F [A∪B] = F [A]∪F [B]
以下是重新使用 LaTeX 语法打印上述内容:
\(F[A \cap B] \subseteq F[A] \cap F[B]\)
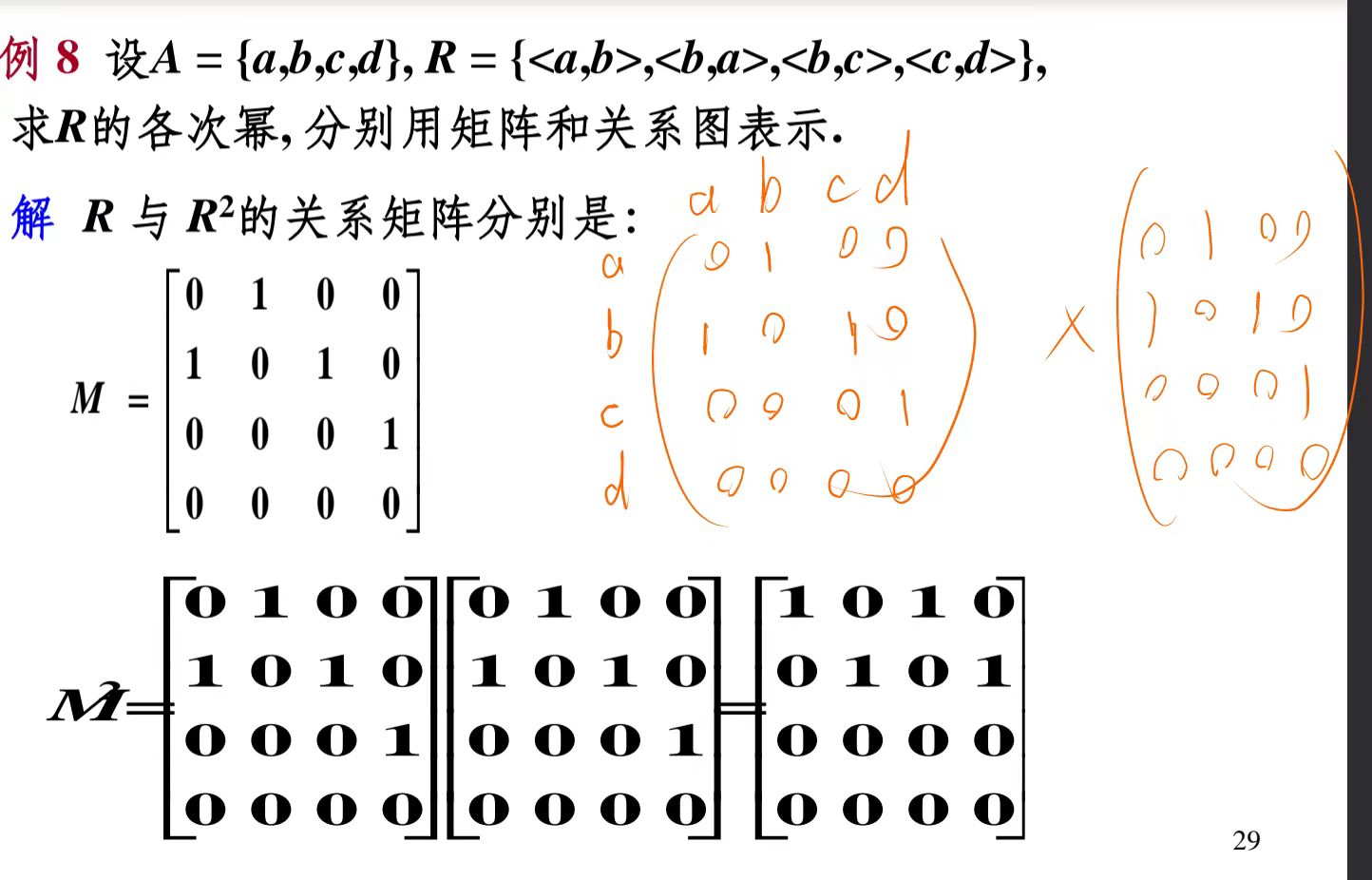
关系的幂运算
本质上比如已知关系集合,就是以每个有序对的第一个元素A为起点,看经过有序对的第二个元素B能到达哪个终点C,有序对<A, C>就是新的关系集合里的一个元素
定义
\(R^0 = \{ (x,x) \mid x \in A \} = I_A\)
\(R^{n+1} = R^n \circ R\)
举例:

幂运算的性质
循环
设 A 为 n 元集, R 是A上的关系, 则存在自然数 s 和 t, 使得\(R^s = R^t\).
幂的相加和想乘
\(R^m \circ R^n = R^{m+n}\)
\((R^m)^n = R^{mn}\)
关系的性质
自反与反自反
定义
自反就是这种关系能让元素x得到自己本身,反自反就是得不到
举例:

关系矩阵与关系图
1. 自反的关系矩阵主对角线元素都是1
2. 自反的关系图每个节点都有自回路
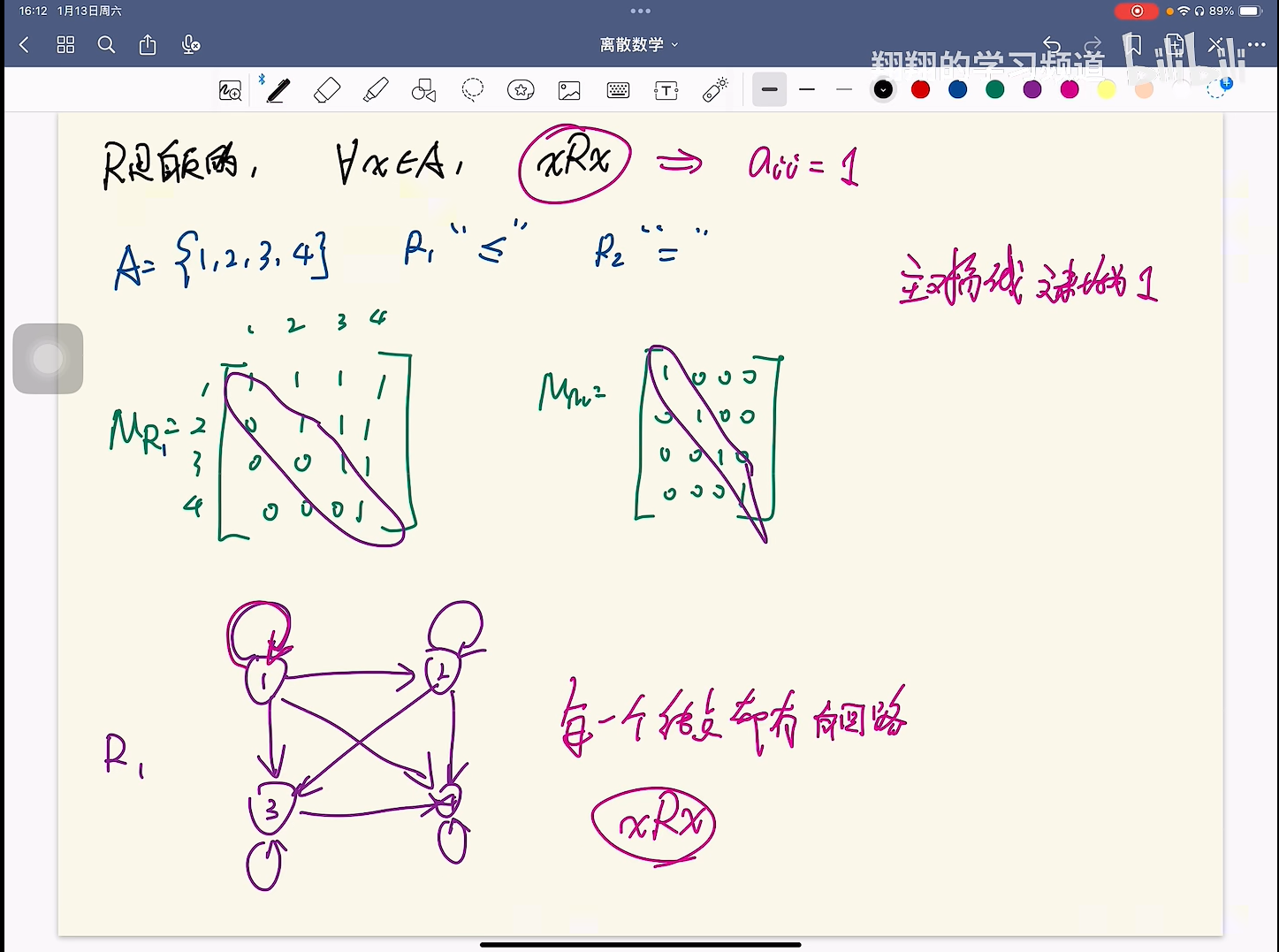
反自反关系关系矩阵主对角线都是0,关系图每个节点没有自回路
对称与反对称
定义
对称关系就是两个不同的元素x和y在交换位置后关系依然满足,反对称就是两个元素x和y只有在相等时才能实现
对称是2个不同元素,自反是1个元素
关系矩阵与关系图
对称关系
1. 对称关系关系矩阵关于主对角线对称
2. 对称关系关系图有成对的有向边
反对称关系
1. 反对称关系的关系矩阵中除了对角线,\(a_{ij}与a_{ji}\)不能同时为1
2. 反对称关系的关系图两个节点之间最多只有1条有向边
传递
关系的闭包
定义
关系闭包个人理解就是在原来关系集合R基础上加上尽可能少的关系,组成新集合R',新集合R’满足自反或者对称或者传递

构造闭包
自反闭包r
就是并上一个恒等关系
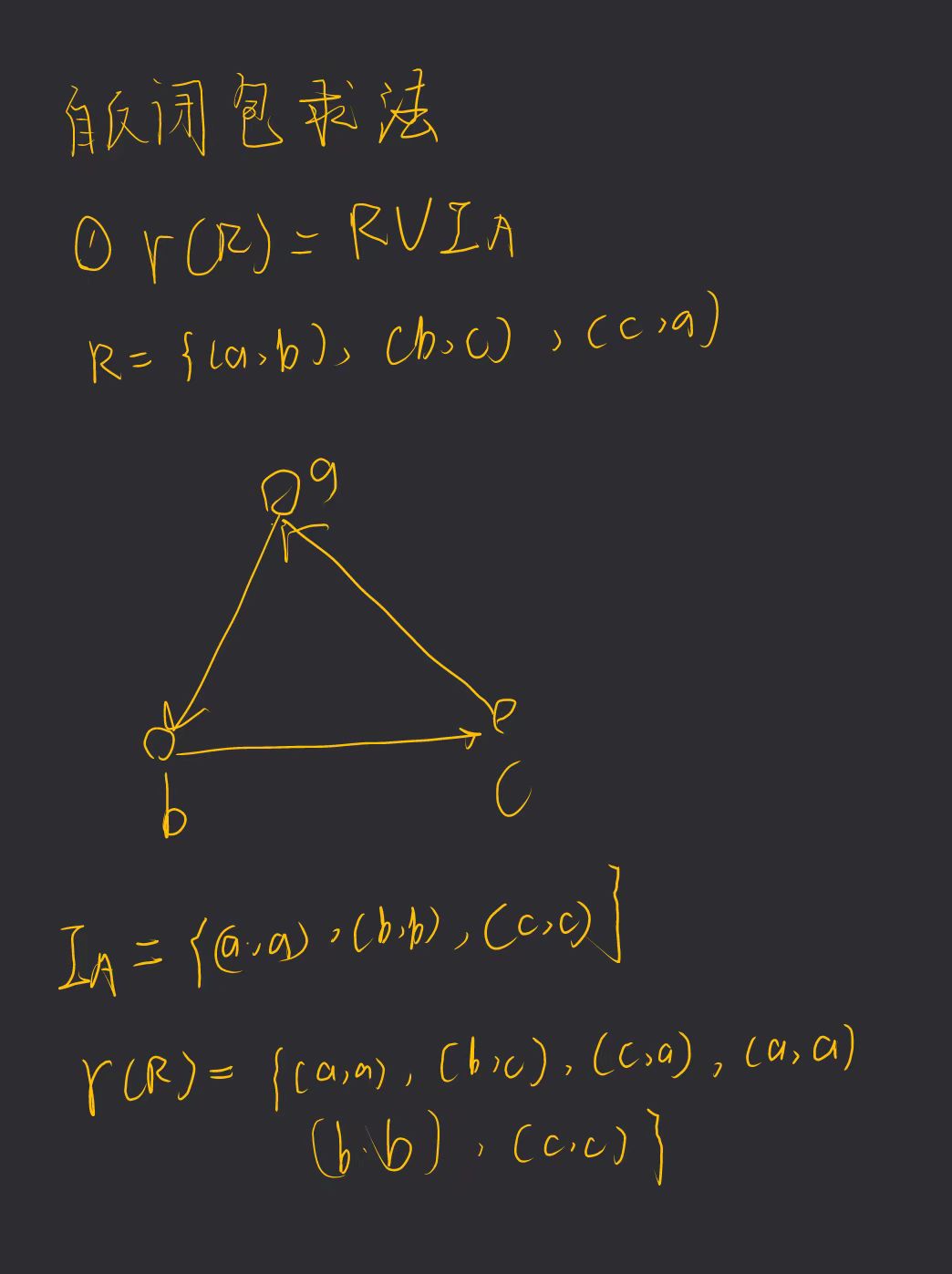
对称闭包s
就是并上一个逆关系
传递闭包t
传递闭包就是将所有独立的幂(就是有的幂最后循环是一样的)并起来,一般就是算到R的某个幂变成恒等关系就行
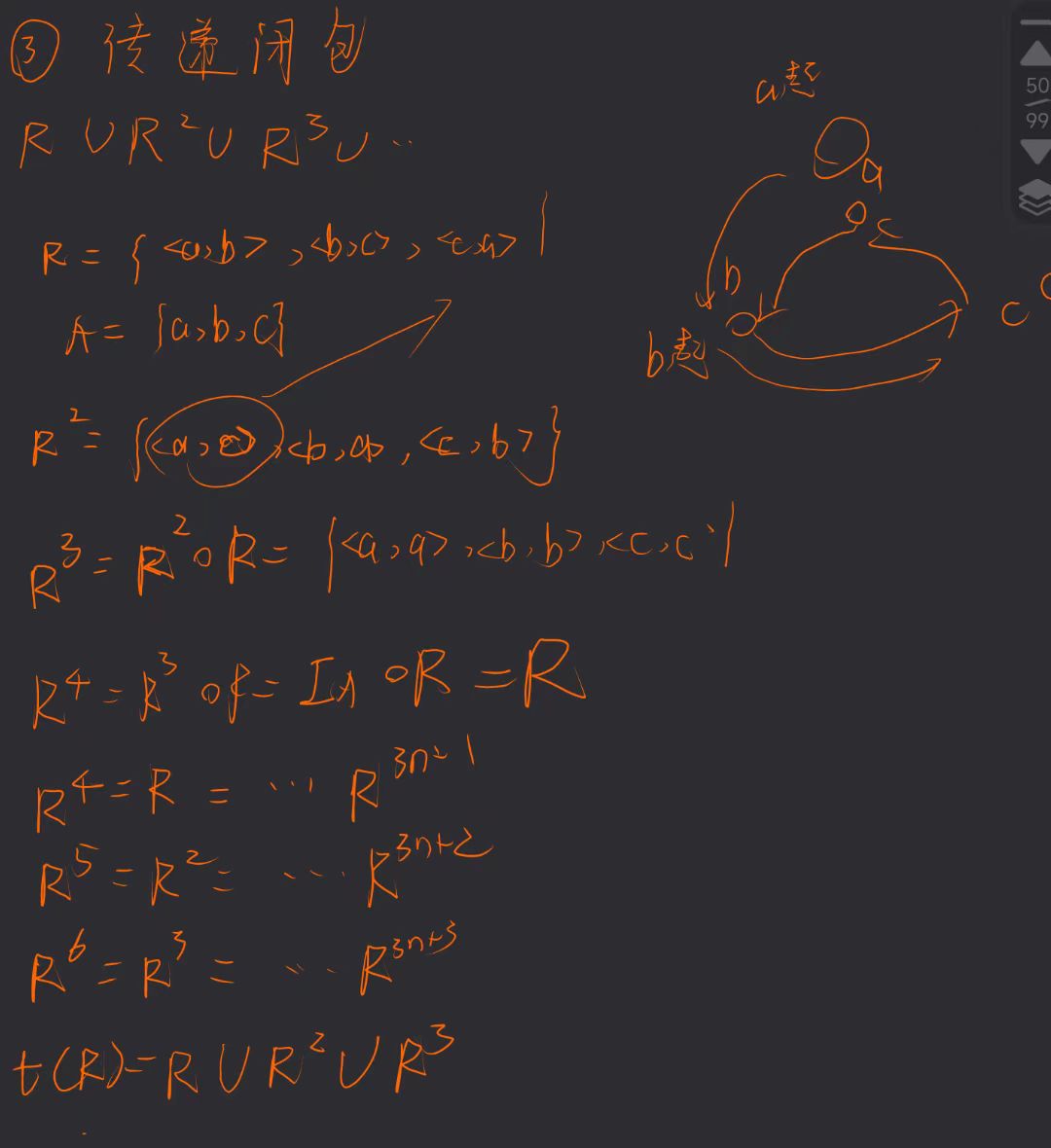
warshall算法
举例:
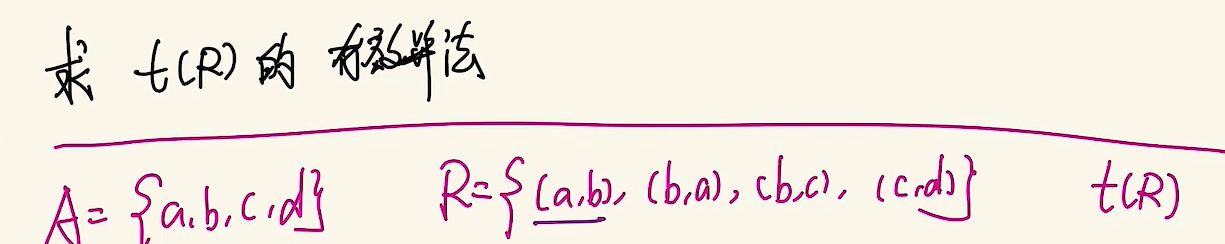
"看列加行"
- 这里的加是逻辑加(就是或)
- 看一列,这一列如果有1,将对应的行加到另一行
闭包的性质
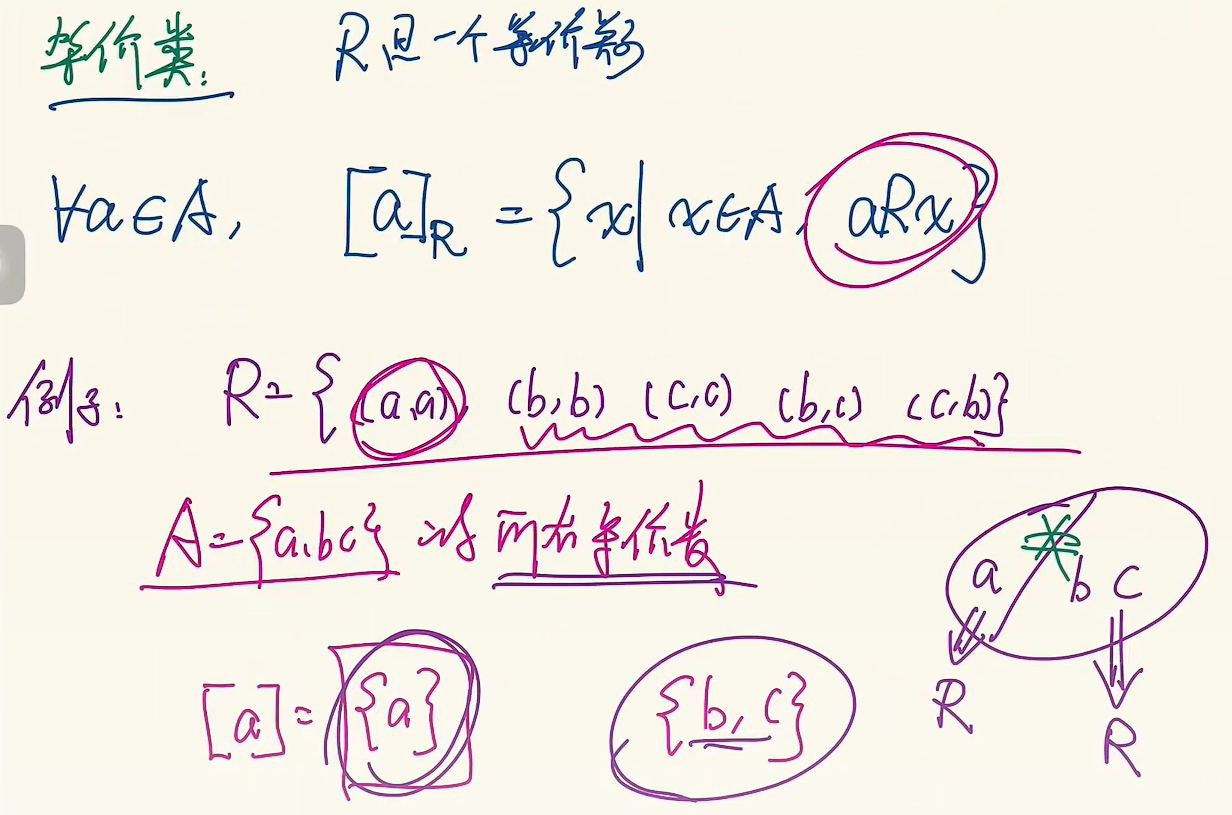
等价类
等价关系
定义
满足:自反、对称、传递的关系
举例:

首先根据(a - b)/3将所有有序对列出,然后根据关系图说明
模n同余
模n同余的定义

证明模n同余是等价关系
关键就是证明不同形式的k(-k,k+t)属于整数Z
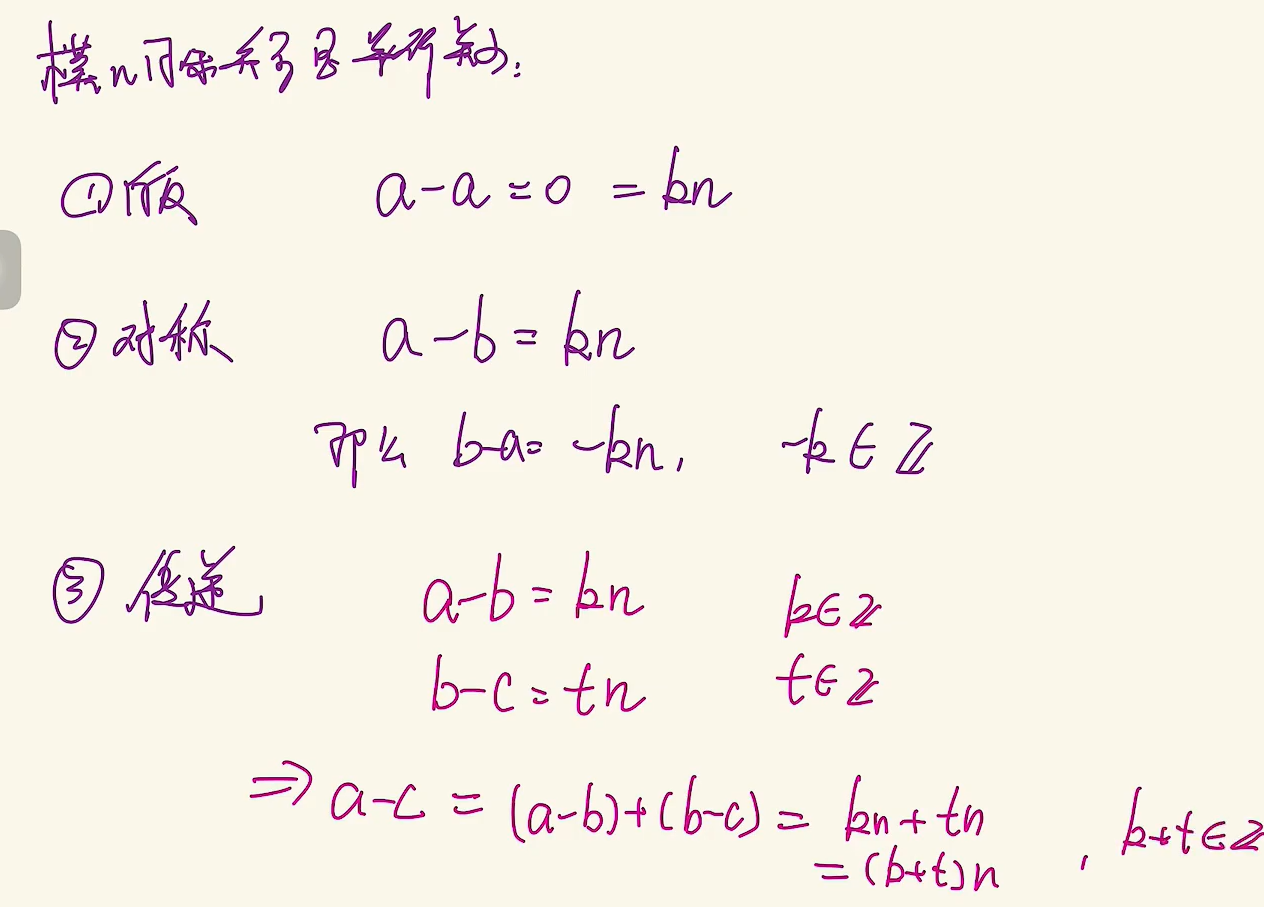
等价类
定义

任意在A中的元素a的等价类,就是在任意在A中的元素x,a和x都满足某种关系,这些x集合就是a的等价类,比如模7同余,那么所有余数为0的就是一个等价类。0, 7, 14这些都满足模7余0,它们就是一个等价类;1, 8, 15都满足模7余1,它们就满足一个等价类。但是7,8之间不满足一个等价类
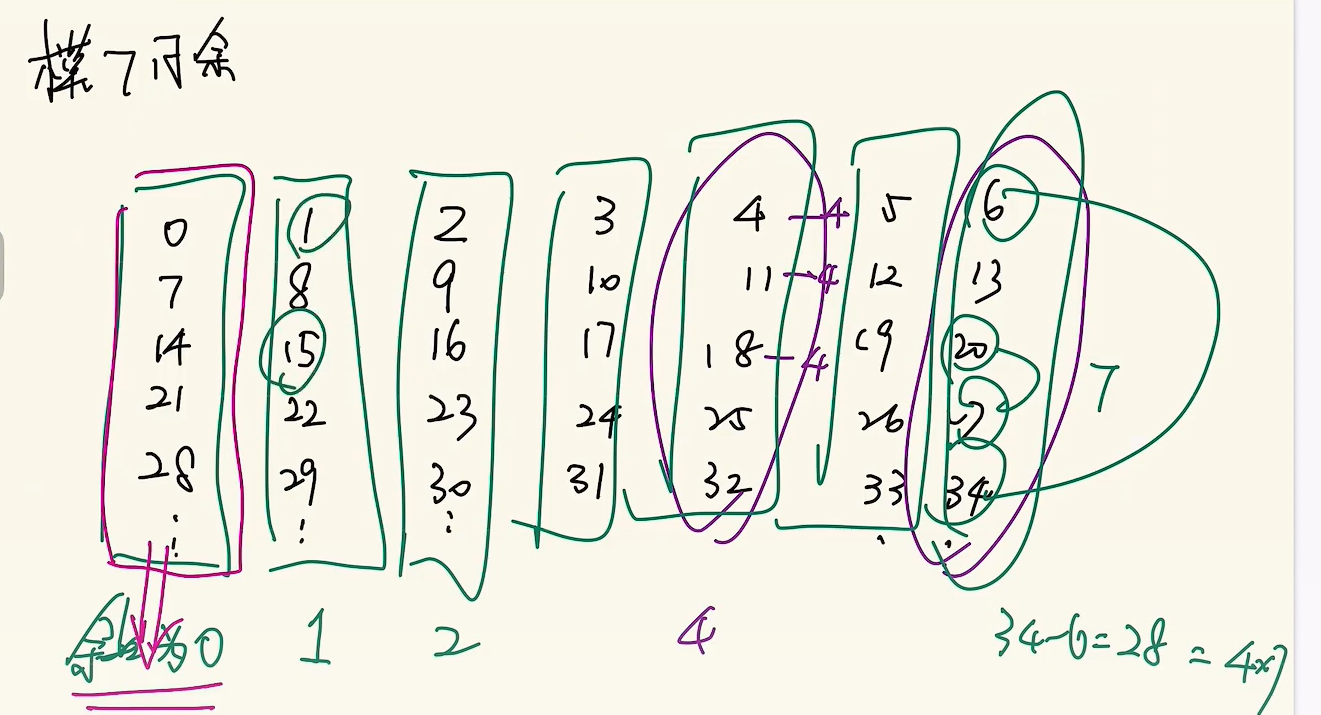
更抽象点如下图,其中和a有关系的只有a,所以a的等价类中只有a,与b有关系的有b和c,与c有关系的有b和c,所以b的等价类有b,c,同理c的等价类有b,c
商集
定义:
将等价类中的每个类当做一个元素。本来一个等价类是一个集合,现在将这个集合看做一个元素
偏序关系
视频讲解:偏序关系与偏序集、Hasse图、极大元、极小元、全序关系、最大元、良序集
定义
对于“比较大小”这种关系的推广
性质
- 自反性
- 反对称性
- 传递性
注:偏序关系和等价关系区别
举例1:证明包含关系是偏序关系:
- 证明自反性
- 证明传递性
- 证明反对称性

举例2:证明整除关系是偏序关系

关键是证明反对称
思路是证明只有两个相等才满足关系

覆盖
y如果盖住了x,y和x之间不会有z能满足大小关系,x和y近邻
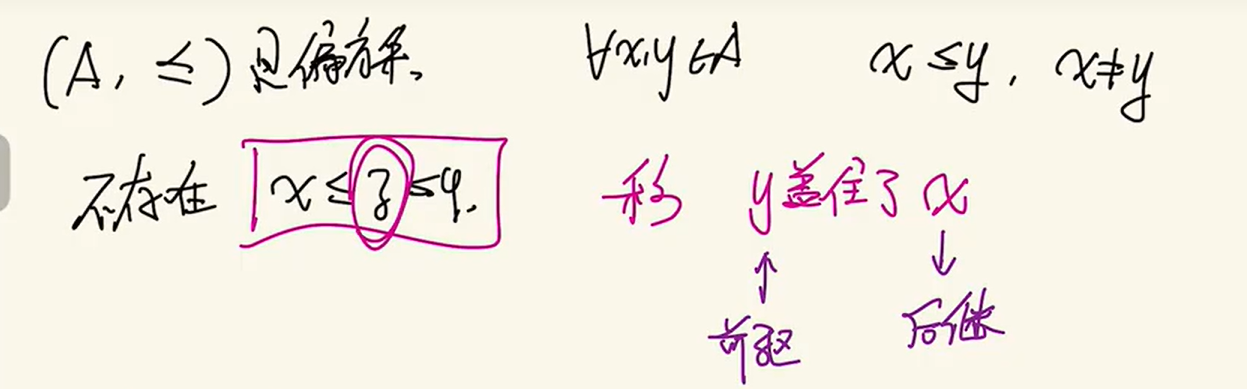
举例:
整除关系下的覆盖关系

2能整除6,4不能整除6,所以2和6之间也是覆盖关系
哈斯图
定义

上面的哈斯图
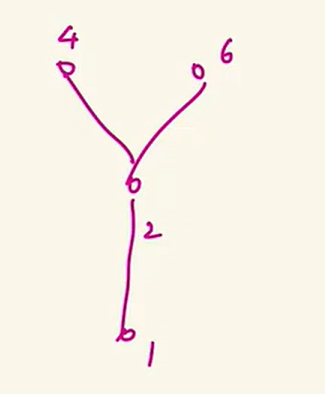
最大元和最小元,极大元和极小元
最小元:里面每个元素都比这个元素“大”
最大元:里面每个元素都比这个元素“小”
注:最大元和最小元唯一
极小元:找不到更小的,但是不一定每个元素都比这个元素“大”,因为有的元素和它没有“大小”关系
极大元:找不到更大的,但是不一定每个元素都比这个元素“小”,因为有的元素和它没哟“大小”关系


