定点数的表示
无符号数和有符号数
无符号数:
整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值。
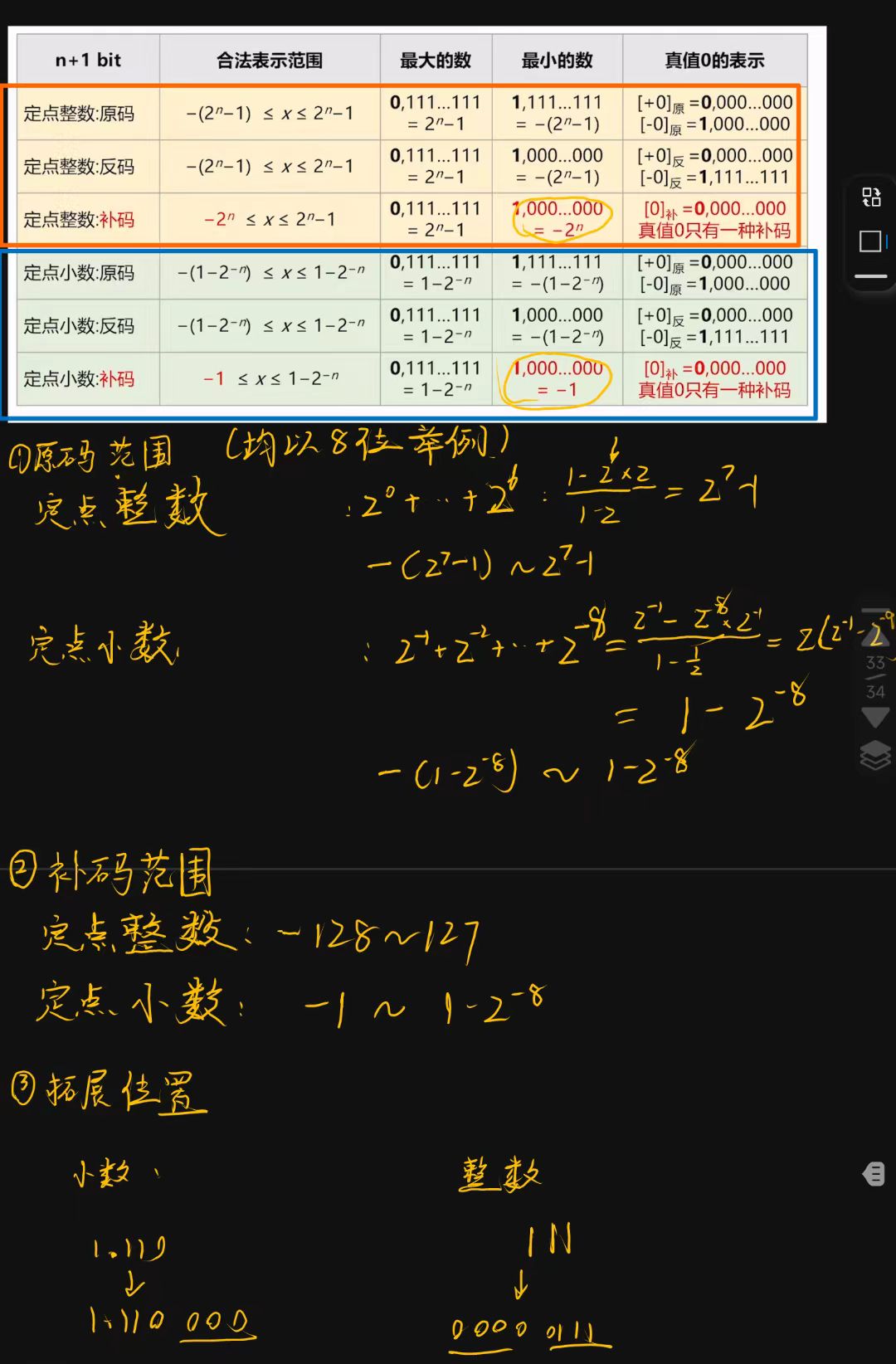
n位无符号数的表示范围是\(0 \sim2^n - 1\)

有符号数
真值:该数字的实际值,包含正负;
机器数:用数字表示正负号的二进制数
定点小数:约定符号位后面就是小数点
- +0.75D = 0.11B
- -0.75D =1.11B
定点整数:约定小数点在数值的最后
- +3D = 011.B
- -3D = 111.B
定点整数和定点小数区别和联系
原码、补码、反码、移码
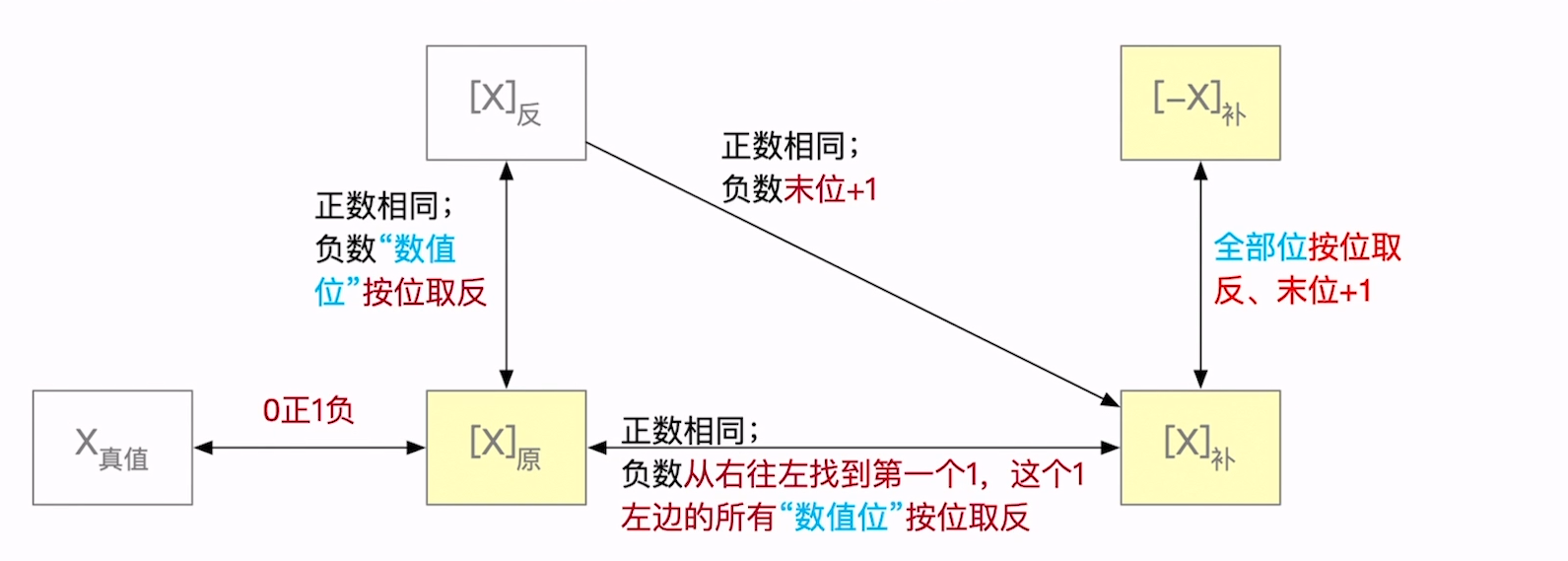
原码

补码
补码数值位不能解读为位权,而应该先转换为原码
补码的-128无法转换成原码
求一个数的相反数的补码的另类小技巧
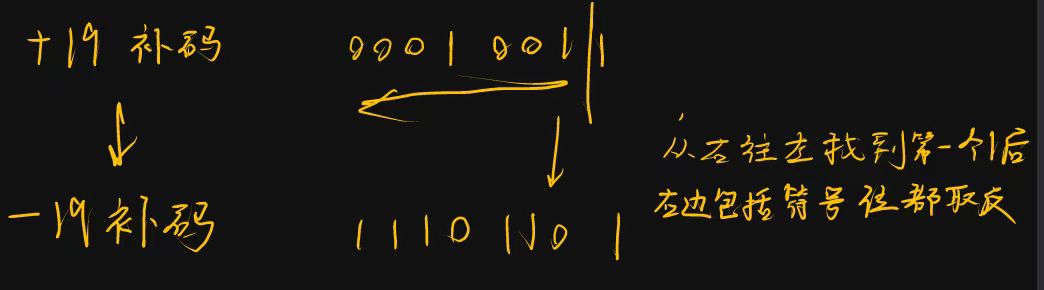
关于补码正儿八经的解释
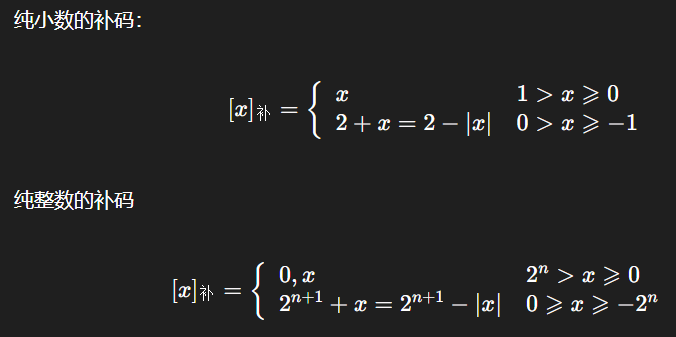
整数方面,负数的补码的求法就是用二进制上比当前数二进制多1位,多出来的高位是1减去当前数的绝对值
举例:

不同码之间相互转换
定点数的运算
定点数的移位运算
算术移位
原码
符号位保持不变,仅对数值位进行移位。
右移:高位补0,低位舍弃。若舍弃的位=0,则相当于-2;若舍弃的位0,则会丢失精度
左移:低位补0,高位舍弃。若舍弃的位=0,则相当于x2:若舍弃的位0,则会出现严重误差
反码
正数与原码相同,负数补1
举例: 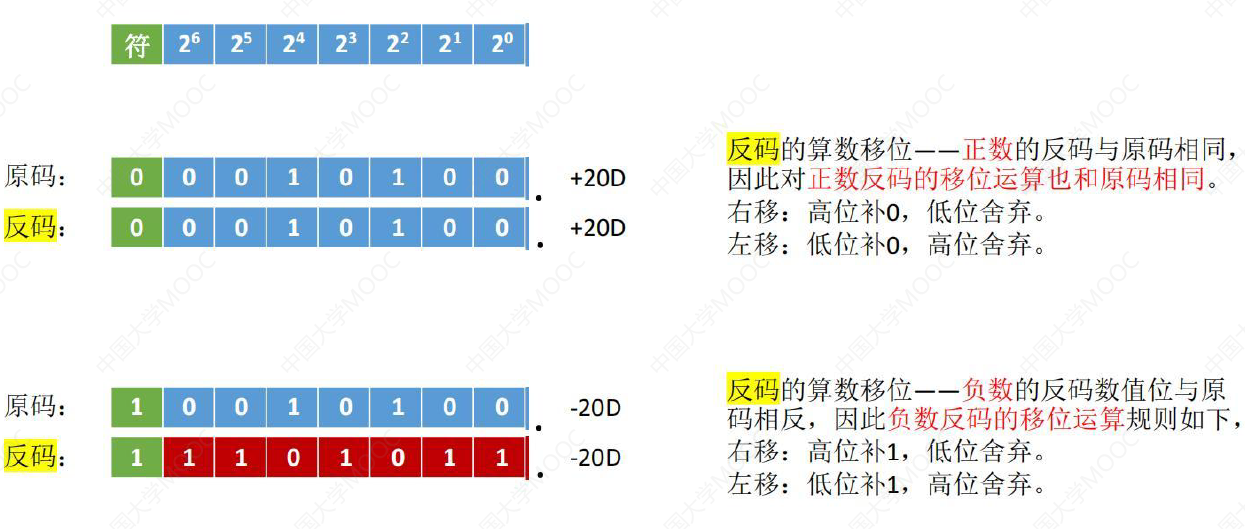
补码
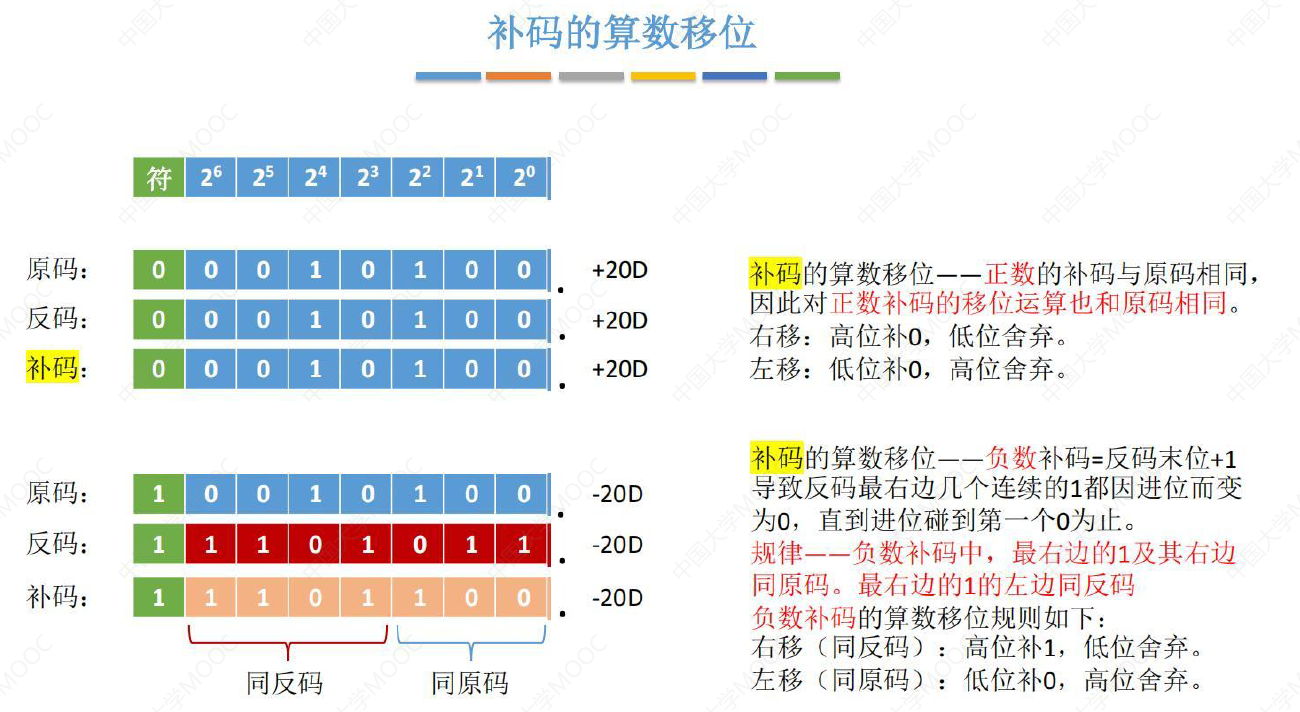
正数与原码相同
负数右移,高位出现空位,高位与反码相同,所以补1
负数左移,低位出现空位,低位与原码相同,所以补0
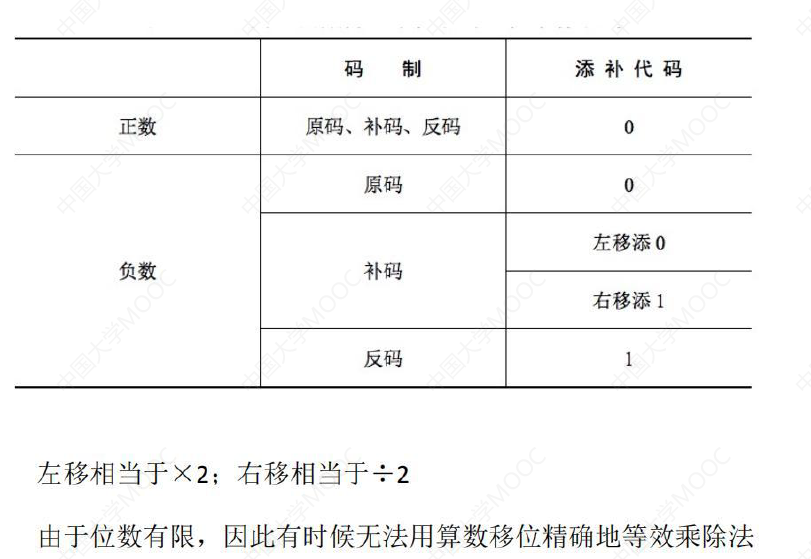
不同码算术移位的一个总结(重要!!!)
1. 如果是正数,无论什么码都补0
2. 如果是负数,原码都补0,与之相对的反码都补1,补码左移补0,右移补1
逻辑移位
都补0,区别算术移位和逻辑移位的理解,算术运算比逻辑运算复杂
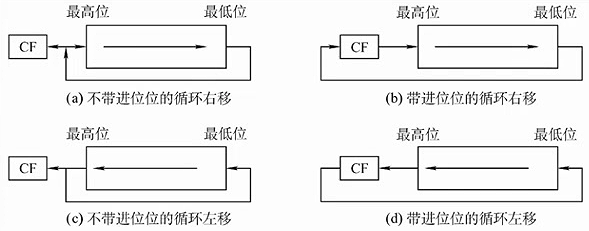
循环移位
加减法
全部转换得到补码后相加,其中减法就是转换成相反数的的补码后再相加(无论有符号数还是无符号数,都转成补码)
举例:

溢出的概念和判断方式
- 大于机器所能表示的最大正数称为上溢;
- 小于机器所能表示的最小负数称为下溢。
- 当两个符号相同的数相加或者两个符号相异的数相减时才会发生溢出。
对溢出的判断有几种方式:
采用一位符号位

采用一位符号位根据数据位进位情况判断溢出
即“模2补码”。
设符号位的进位 CS,最高数位的进位 C1,则当 CS 和 C1 不同时发生溢出。
采用双符号位
即“模4补码”。
正数符号位为00,负数符号位为11。
记两个符号位分别为 S1 和 S2,则 V = S1 ⊕ S2,若V=0,无溢出;V=1,有溢出。
00:正数无溢出
01:正数有溢出
11:负数无溢出
10:负数有溢出
模4补码存储时仍然为一个符号位,因为正确的表示两位符号位必然是相同的
当送入ALU时,才将原来的符号位同时送入ALU的双符号位中
定点数的乘法运算
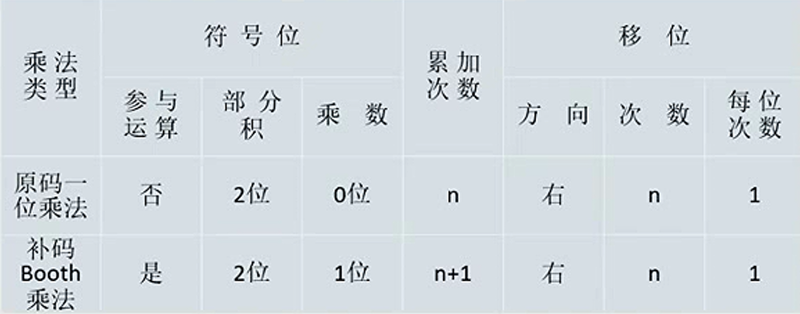
原码一位乘法
被乘数带符号位运算,乘数不需要
移位需要移动乘数的有效位数,最后以移位结束,将乘数全部移除
- 符号位单独处理:乘数与被乘数异或
- 绝对值相乘
- ACC存放乘积高位,MQ存放乘数、乘积低位,X存放被乘数
- 每次看MQ中最低位
- 为1,ACC加上被乘数
- 为0,ACC加上0
- 每次运算后右移一位,高位补0
- 直到MQ仅剩原符号位,舍去不参与运算
- 小数点位于ACC第一位(乘积符号位)后
补码一位乘法
乘数增加了一个辅助位,原来表示数值的有n位,表示符号的有1位,现在增加了一个辅助位,变成n+2位。
被乘数和存储结果的也增加1位,所以用双符号位
1. 双符号位
2. 算术右移
3. 三种选择

定点数除法运算
原码恢复余数法
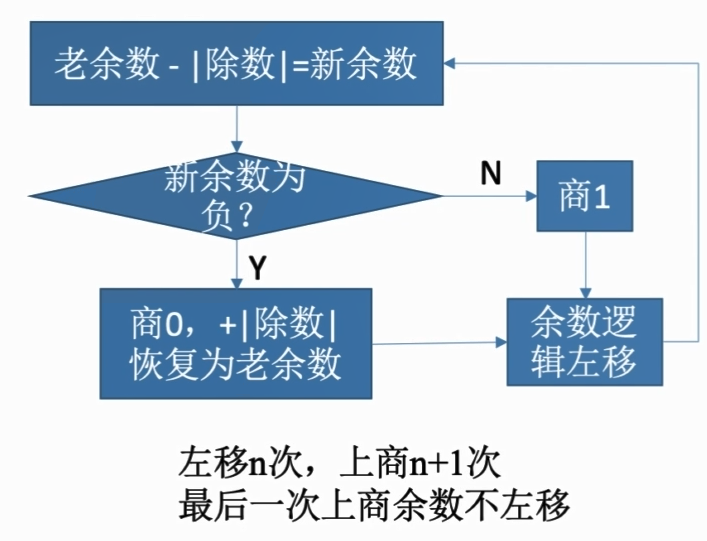
原码加减交替法
原码除法两种方法在处理商1发现余数是0时采取操作的比较:
恢复余数法:当余数为负时商0,并+|除数|(为了恢复余数)再左移,再-|除数|,才能得到新余数和对应的商
加减交替法:当余数为负时商0,并左移,再+|除数|,就能得到新余数和对应的商
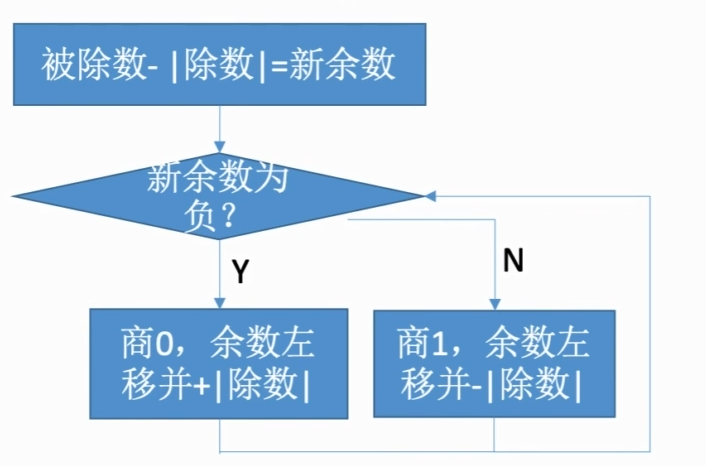
补码加减交替法
- 符号位参与运算
- 被除数/余数、除数采用双符号位
- 被除数和除数同号,则被除数减去除数;异号则被除数加上除数。
- 余数和除数同号,商1,余数左移一位减去除数;余数和除数异号,商0,余数左移一位加上除数。重复n次
- 商末尾恒为1

整数型及类型转换
长整数变为短整数:0x000286a1 --> 0x86a1(截断高位)
短整数变为长整数:符号扩展
有符号数变为无符号数:0xef1f(真值-3421) --> 0xef1f(真值61215)不改变数据内容,改变解释方式