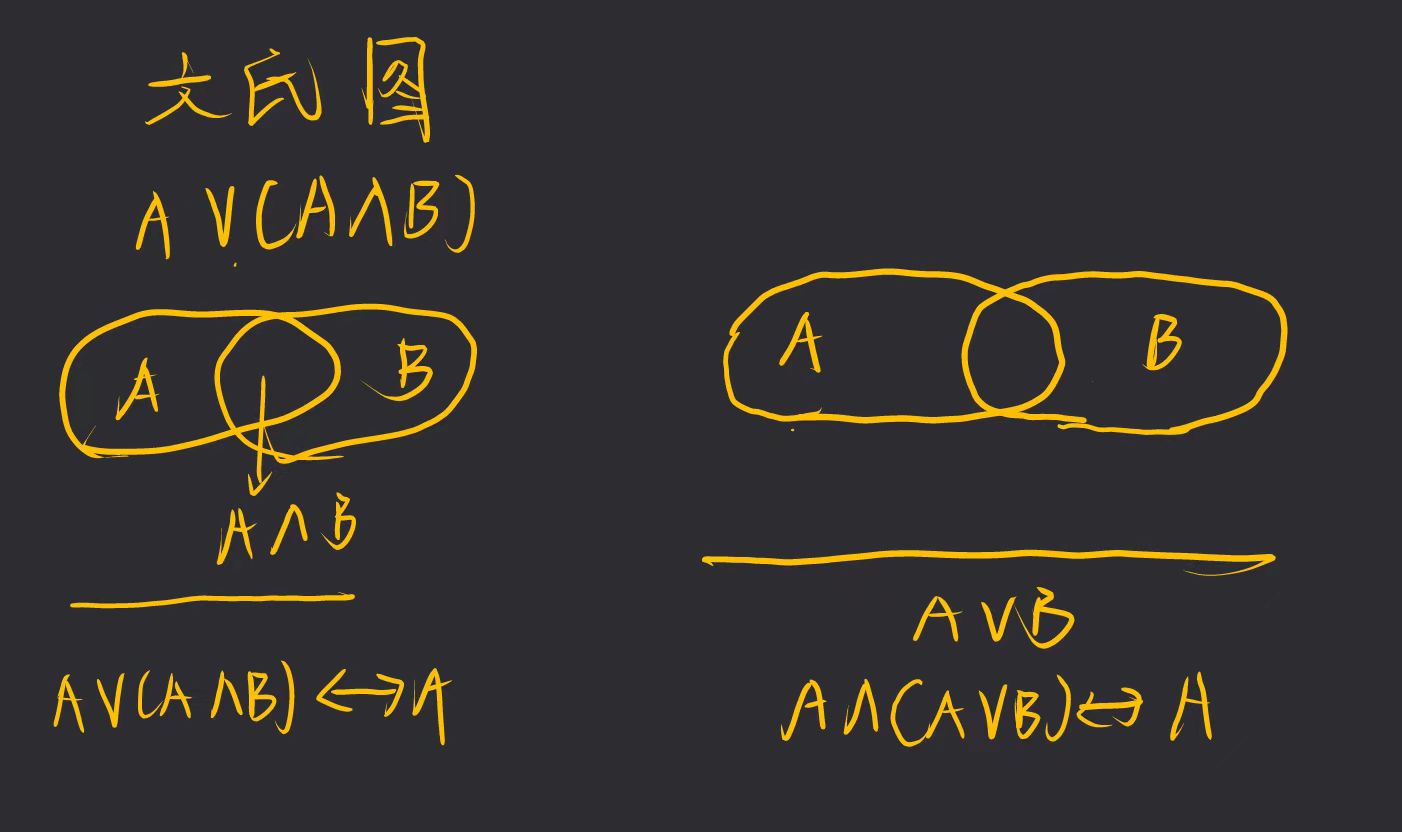Pilot's Blog
0%

第二章-命题逻辑等值演算

发表于 更新于 分类于 ， Valine：
本文字数： 4.1k 阅读时长 ≈ 4 分钟

等值式与基本的等值式

等值式定义

如果A\(\leftrightarrow\)B是永真式(重言式)，则称A与B等值

注：

  1. 哑元

举例

  1. 判断两个公式是否等值

基本等值式

双重否定律: ¬(¬A) ↔︎ A

幂等律: A ∨ A ↔︎ A, A ∧ A ↔︎ A

交换律: A ∨ B ↔︎ B ∨ A, A ∧ B ↔︎ B ∧ A

结合律: (A ∨ B) ∨ C ↔︎ A ∨ (B ∨ C), (A ∧ B) ∧ C ↔︎ A ∧ (B ∧ C)

分配律: A ∨ (B ∧ C) ↔︎ (A ∨ B) ∧ (A ∨ C), A ∧ (B ∨ C) ↔︎ (A ∧ B) ∨ (A ∧ C)

德摩根律: ¬(A ∨ B) ↔︎ (¬A) ∧ (¬B), ¬(A ∧ B) ↔︎ (¬A) ∨ (¬B)

吸收律: A ∨ (A ∧ B) ↔︎ A, A ∧ (A ∨ B) ↔︎ A

注：吸收律的理解记忆：文氏图

零律: A ∨ 1 ↔︎ 1, A ∧ 0 ↔︎ 0

同一律: A ∨ 0 ↔︎ A, A ∧ 1 ↔︎ A

排中律: A ∨ ¬A ↔︎ 1

矛盾律: A ∧ ¬A ↔︎ 0

蕴涵等值式: A → B ↔︎ ¬A ∨ B

等价等值式: A ↔︎ B ↔︎ (A → B) ∧ (B → A)

假言易位: A → B ↔︎ ¬B → ¬A

等价否定等值式: A ↔︎ B ↔︎ ¬A ↔︎ ¬B

归谬论: (A → B) ∧ (A → ¬B) ↔︎ ¬A

等值演算与置换规则

置换规则

\(如果 \Phi(A) 是包含公式 A 的命题公式， \Phi(B) 是将公式 B 替换为 \Phi(A) 中所有的 A 后得到的命题公式，则若 B \leftrightarrow A ，则 \Phi(B) \leftrightarrow \Phi(A)。\)

等值演算应用举例

  1. 证明两个公式等值

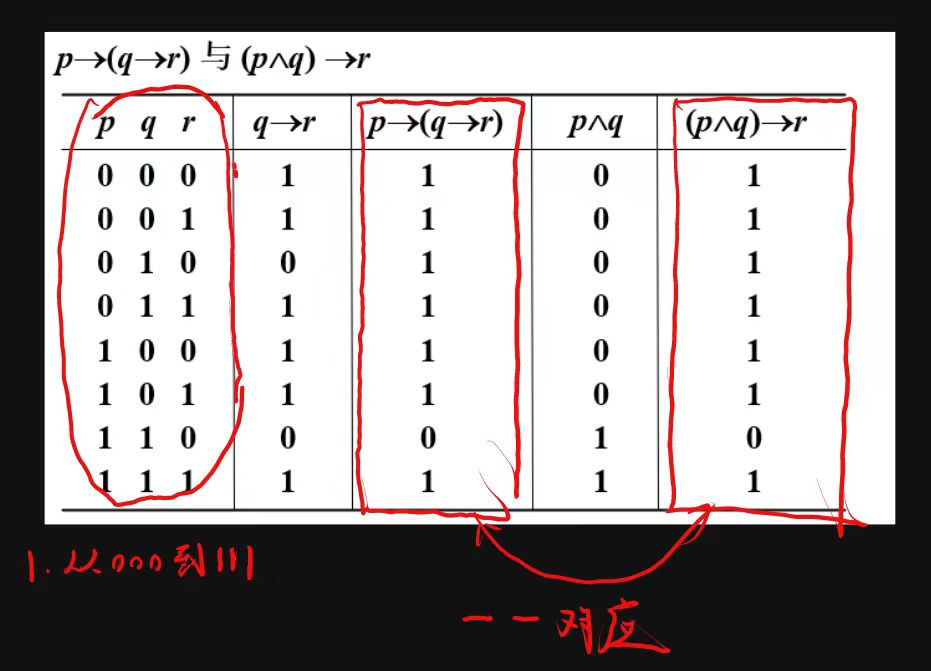
    比如证明\(p \rightarrow (q \rightarrow r) \leftrightarrow (p \land q) \rightarrow r\)

​ 注：用等值演算不能直接证明两个公式不等值

​ 证明两个公式不等值的方法：

​ 举个例子：\(p \rightarrow (q \rightarrow r) \quad 与 \quad (p \rightarrow q) \rightarrow r\)

​ ①真值表

​ ②观察:000左真右假

​ ③先用等值化简再观察

  1. 判断公式类型

    \(q \land \neg (p \rightarrow q)\)

析取范式与合取范式，主析取范式与主合取范式

基本概念

文字

命题变项及其否定的总称

简单析取式

由有限个文字构成的析取式。一些例子包括：

  • p
  • \(\neg q\)
  • \(p \lor \neg q\)
  • \(p \lor q \lor r\)
  • ...

简单合取式

由有限个文字构成的合取式。一些例子包括：

  • p
  • \(\neg q\)
  • \(p \land \neg q\)
  • \(p \land q \land r\)
  • ...

析取范式

是由有限个简单合取式组成的析取式。以下是一些例子：

\(p, \quad \neg p \land q, \quad p \lor \neg q, \quad (p \land \neg q) \lor (\neg p \land q \land \neg r) \lor (q \land r)\)

合取范式

由有限个简单析取式组成的合取式。以下是一些例子：

\(p, \quad p \lor \neg q, \quad \neg p \land q, \quad (p \lor q) \land \neg p \land (p \lor \neg q \lor \neg r)\)

范式

析取范式与合取范式的总称

范式的性质

简单范式

  1. 一个简单析取式是重言式当且仅当它同时含有某个命题变项和它的否定式

  2. 一个简单合取式是矛盾式当且仅当它同时含有某个命题变项和它的否定式

复合范式

  1. 一个析取范式是矛盾式当且仅当它每个简单合取式都是矛盾式

  2. 一个合取范式是重言式当且仅当它的每个简单析取式都是重言式

注：单个文字既是简单析取式，又是简单合取式

范式存在定理

任何命题公式都存在与之等值的析取范式与合取范式

求公式的范式

步骤

  1. 消去A中的\(\to\),\(\leftrightarrow\)
  2. 否定连接词\(\lnot\)內移或消去
  3. 分配律

举个例子：(p→¬q)→r

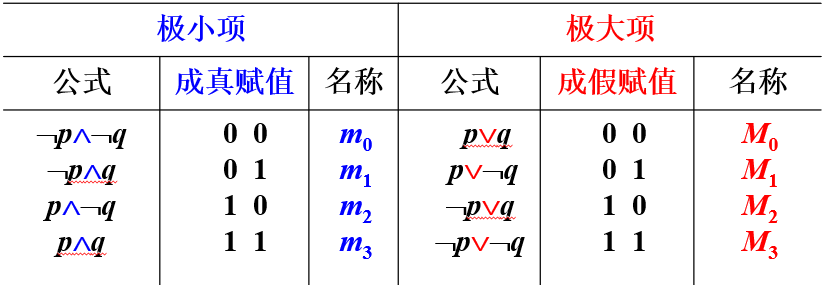
极小项与极大项

定义：

在含有n个命题变项的简单合取式（简单析取式）中，若每个命题变项均以文字的形式在其中出现且仅出现一次，而且第k个文字出现在左起第k位上（1≤k≤n），称这样的简单合取式（简单析取式）为极小项（极大项）。

①每个命题变项均以文字的形式在其中出现且仅出现一次

②第k个文字出现在左起第k位上（1≤k≤n）

③简单合取\(\land\),成真赋值\(\to\)极小项，简单析取\(\lor\)，成假赋值\(\to\)极大项

注：

  1. n个命题变项有\(2^n\)个极小项和\(2^n\)个极大项

  2. 这些极小项（极大项）均互不等值。

  3. 用\(m_i\)表示第i个极小项，其中i是该极小项成真赋值的十进制表示。用\(M_i\)表示第i个极大项，其中i是该极大项成假赋值的十进制表示。\(m_i\)（\(M_i\)）称为极小项（极大项）的名称。

举个例子

主析取范式与主合取范式

主析取范式

由极小项构成的析取范式

主合取范式

由极大项构成的合取范式

例如，n=3，命题变项为 p, q, r 时，

1
2
3
4
5
6
(¬p ∧ ¬q ∧ r) ∨ (¬p ∧ q ∧ r) 
   ⇔ m1 ∨ m3 ——主析取范式

(p ∨ q ∨ ¬r) ∧ (¬p ∨ ¬q ∨ ¬r) 
   ⇔ M1 ∧ M7——主合取范式

求公式主析取范式的步骤:

设公式A含命题变项p1,p2,…,pn。

  1. 求A的析取范式A' = B1 ∨ B2 ∨ … ∨ Bs，其中Bj是简单合取式 j=1,2, … ,s。

  2. 确保每项简单合取式含有n个不同命题变项。若某个Bj既不含pi，又不含¬pi，则将Bj展开成： Bj ⇔ Bj ∧ (pi ∨ ¬pi) ⇔ (Bj ∧ pi) ∨ (Bj ∧ ¬pi) 。重复这个过程，直到所有简单合取式都是长度为n的极小项为止。

  3. 消去重复出现的极小项，即用mi代替mi ∨ mi。

  4. 将极小项按下标从小到大排列。

求公式主范式的步骤

设公式A含命题变项p1,p2,…,pn。

  1. 求A的合取范式A' = B1 ∧ B2 ∧ … ∧ Bs，其中Bj是简单析取式 j=1,2, … ,s。

  2. 确保每项简单合取式含有n个不同命题变项。若某个Bj既不含pi，又不含¬pi，则将Bj展开成： Bj ⇔ Bj ∨ (pi ∧ ¬pi) ⇔ (Bj ∨ pi) ∧ (Bj ∨ ¬pi)。重复这个过程，直到所有简单析取式都是长度为n的极大项为止。

  3. 消去重复出现的极大项，即用Mi代替Mi ∧ Mi。

  4. 将极大项按下标从小到大排列。

举例：

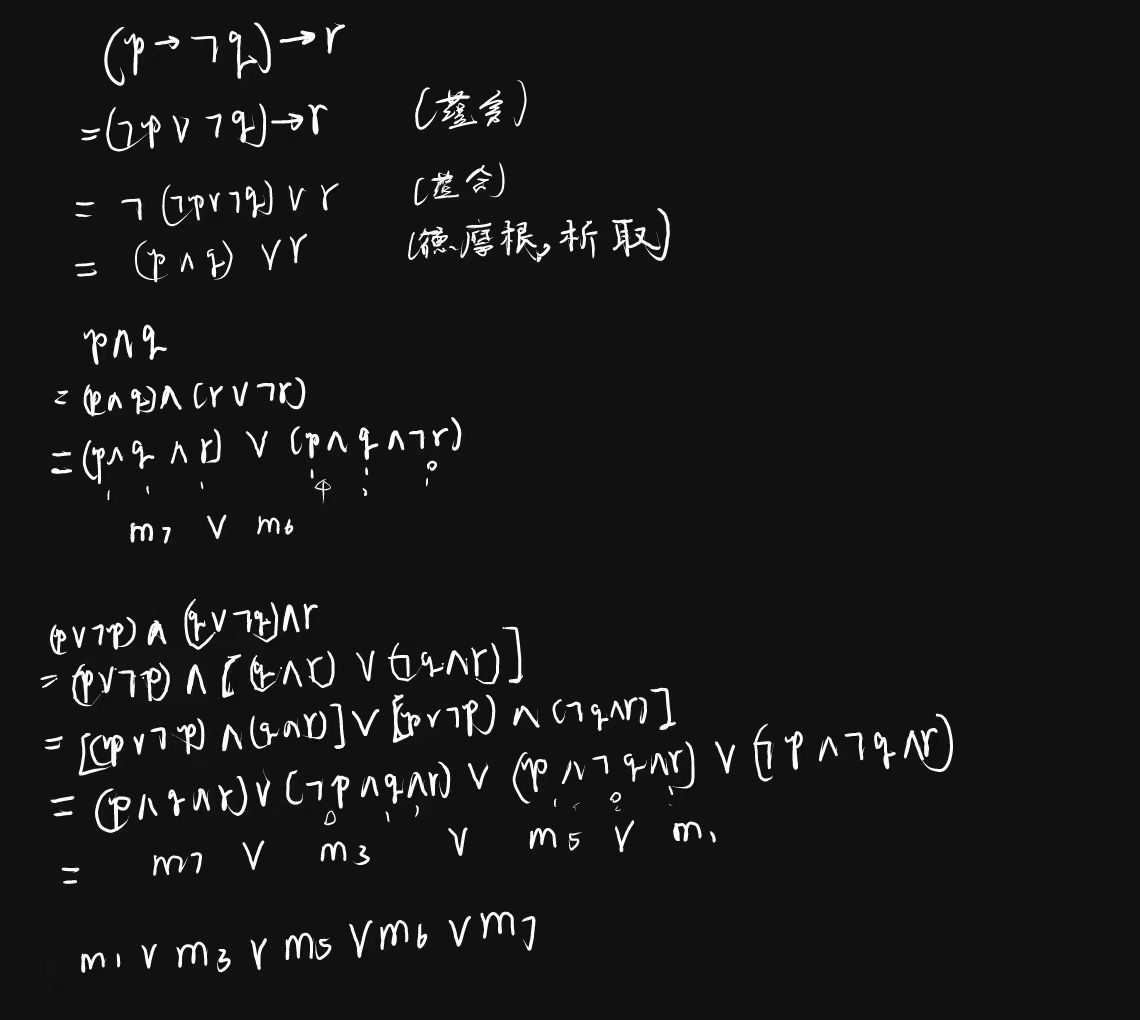
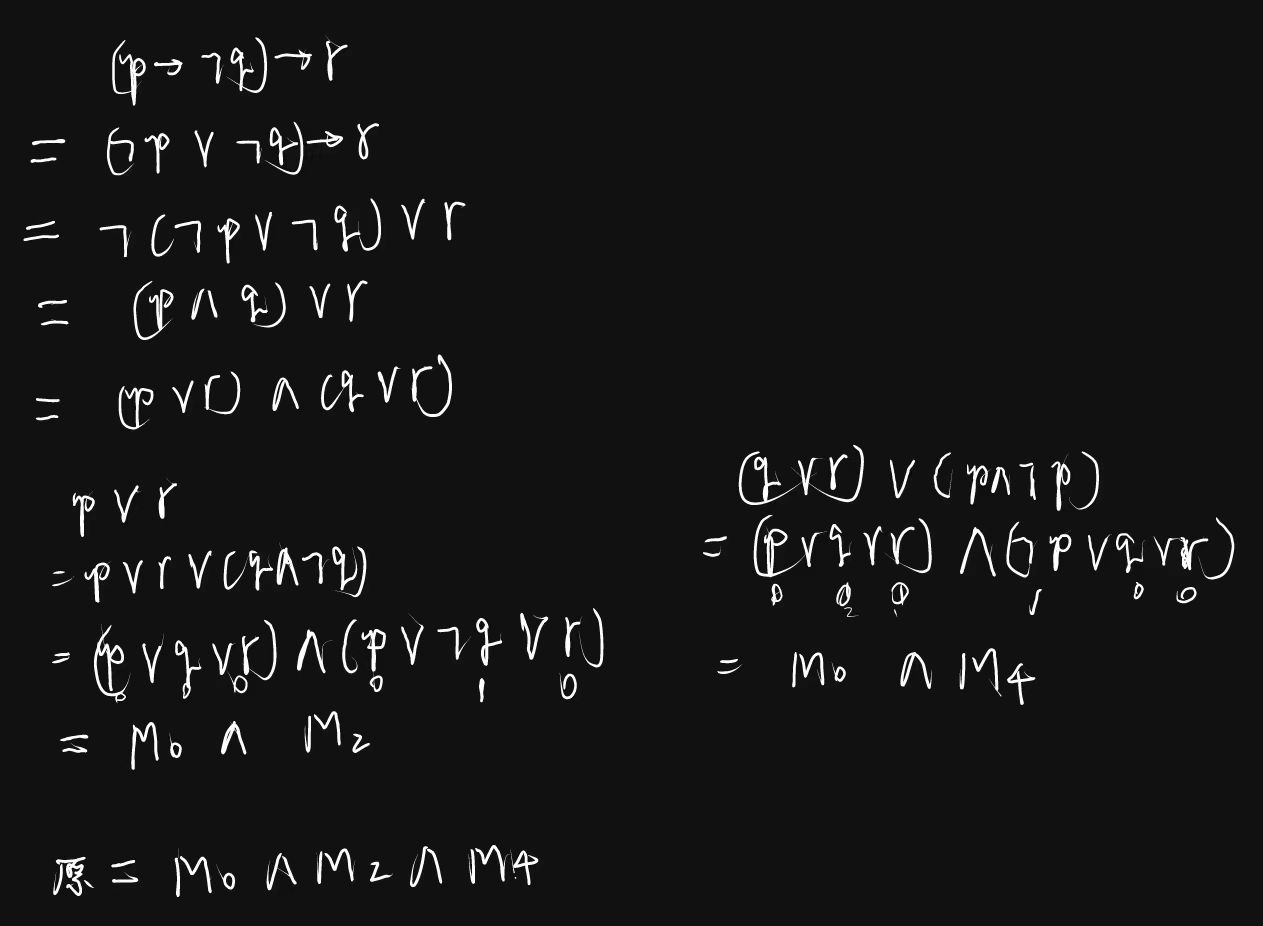
主范式的应用

求公式的成真成假赋值

举例：(p→¬q)→r

由上面可知

(p→¬q)→r ⇔ m1∨m3∨m5∨m6∨m7

成真赋值为 001, 011, 101, 110, 111， 成假赋值为 000, 010, 100.

判断公式的类型

A为重言式 ⇔ A的主析取范式含全部\(2^n\)个极小项 ⇔ A的主合取范式不含任何极大项，记为1.

A为矛盾式 ⇔ A的主合析取范式含全部\(2^n\)个极大项 ⇔ A的主析取范式不含任何极小项，记为0.

A为非重言式的可满足式
⇔ A的主析取范式中至少含一个，但不是全部极小项 ⇔ A的主合取范式中至少含一个，但不是全部极大项.

举例

  1. A ⇔ ¬(p→q)∧q
  2. B ⇔ p→(p∨q)
  3. C ⇔ (p∨q)→r

解实际问题

例9 某单位要从A,B,C三人中选派若干人出国考察, 需满足下 述条件: (1) 若A去, 则C必须去; (2) 若B去, 则C不能去; (3) A和B必须去一人且只能去一人. 问有几种可能的选派方案?

用成真赋值和成假赋值确定主范式

例10 设A有3个命题变项, 且已知A= m1∨m3∨m7, 求A的主合取范式.

解 A的成真赋值是1,3,7的二进制表示, 成假赋值是在主析取 范式中没有出现的极小项的下角标0,2,4,5,6的二进制表示, 它 们恰好是A的主合取范式的极大项的下角标, 故 A ⇔ M0∧M2∧M4∧M5∧M6

主析取范式和主合取范式下标"互补"

联结词完备集

联结词完备集

定义2.7 设S是一个联结词集合，如果任何n(n≥1) 元真值函数都可以由仅含S中的联结词构成的公式表示，则称S是联结词完备集

若S是联结词完备集, 则任何命题公式都可由S中的联结词表示

定理2.6 S = {¬, ∧, ∨}是联结词完备集

复合联结词

定义2.8 设 p, q 为两个命题, 非(p且q)称作p与q的与非式, 记作 p↑q, 即 p↑q ⇔ 非(p且q), ↑称为与非联结词。非(p或q)称作p与q的或非式, 记作 p↓q, 即 p↓q ⇔ 非(p或q), ↓称为或非联结词。

定理2.7 {↑}与{↓}为联结词完备集。

证明：{非, 且, 或}为完备集

非p ⇔ 非p且非p ⇔ 非(p或p) ⇔ p↓p

p且q ⇔ 非(非p或非q) ⇔ 非p↓非q ⇔ (p↓p)↓(q↓q)

p或q ⇔ 非非(p或q) ⇔ 非(p↓q) ⇔ (p↓q)↓(p↓q)

得证{↓}为联结词完备集。对{↑}类似可证。

可满足性问题与消解法

空简单析取定义：不含任何文字的简单析取式称作空简单析取式，记作λ。规定λ是不可满足的。

常见字母和含义：

S: 合取范式,

C: 简单析取式,

l: 文字,

α: 赋值,

公式可带下角标或 ′

文字 l 的补 lc: 若 l = p，则 lc = ¬p；若 l = ¬p，则 lc = p。

S\(\approx\)S': S 是可满足的当且仅当 S' 是可满足的

消解式定义： 设 C1 = λ ∨ C1'，C2 = λc ∨ C2'，其中 C1' 和 C2' 不含 λ 和 λc，称 C1' ∨ C2' 为 C1 和 C2（以 λ 和 λc 为消解文字）的消解式或消解结果，记作 Res(C1, C2)。

消解式举例：Res(¬p ∨ q ∨ r, p ∨ q ∨ ¬s) = q ∨ r ∨ ¬s，观察可知没有p

消解步骤：

  1. 将公共字母且互为“相反数”的两个字母消去，比如上面的p
  2. 将剩下字母用∨连接

消解序列与合取范式的否证

消解序列的定义：设 S 是一个合取范式，C1, C2, ..., Cn 是一个简单析取式序列。如果对每一个 i (1 ≤ i ≤ n)，Ci 是 S 的一个简单析取式或者是 Res(Cj, Ck) (1 ≤ j < k < i)，则称此序列是由 S 导出 Cn 的消解序列。当 Cn = λ 时，称此序列是 S 的一个否证。

上面说白了就是消解到最后字母没了那么就是否证，否证又说明是不可满足

举个例子：

消解算法

  1. 将\(S_0和S_2设置为空集，S_1设置为原式S中的析取式的集合\)
  2. 每轮循环先将\(S_0\)与\(S_1\)中元素进行消解运算，再将\(S_1\)自己与自己消解，运算得到的结果如果没有字母就退出循环，说明不可消解，如果消解结果既不在\(S_0\)中也不在\(S_1\)中就与\(S_2\)取并集
  3. 一轮消解后将S1赋给\(S_0\),\(S_2\)赋给\(S_1\),\(S_2\)重置为空集。直到一轮循环后\(S_2\)还是空集循环结束输出yes

举个例子