算法复杂性分析
算法渐近复杂性
渐近(不严格小/大)
渐近上界\(O\)

渐进下界\(\Omega\)

非紧(严格小/大)
非紧上界\(\omicron\)

非紧下界\(\omega\)

紧渐近界\(\Theta\)

注:上面符号与其说表示的是一个函数,不如说表示的是一个函数簇
总结

渐近的性质
传递性

反身性
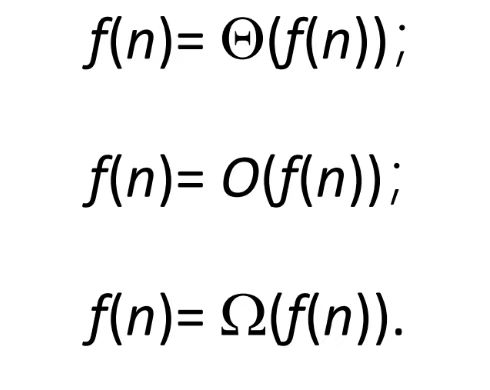
互对称性:一个是另一个的上界,另一个就是一个的下界
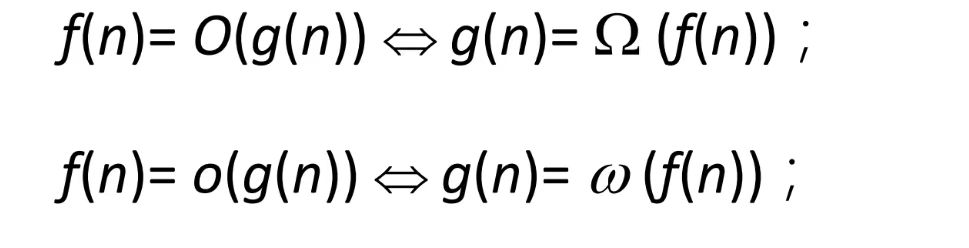
对称性
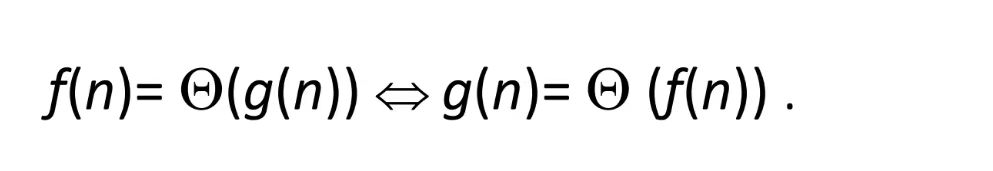
算术运算
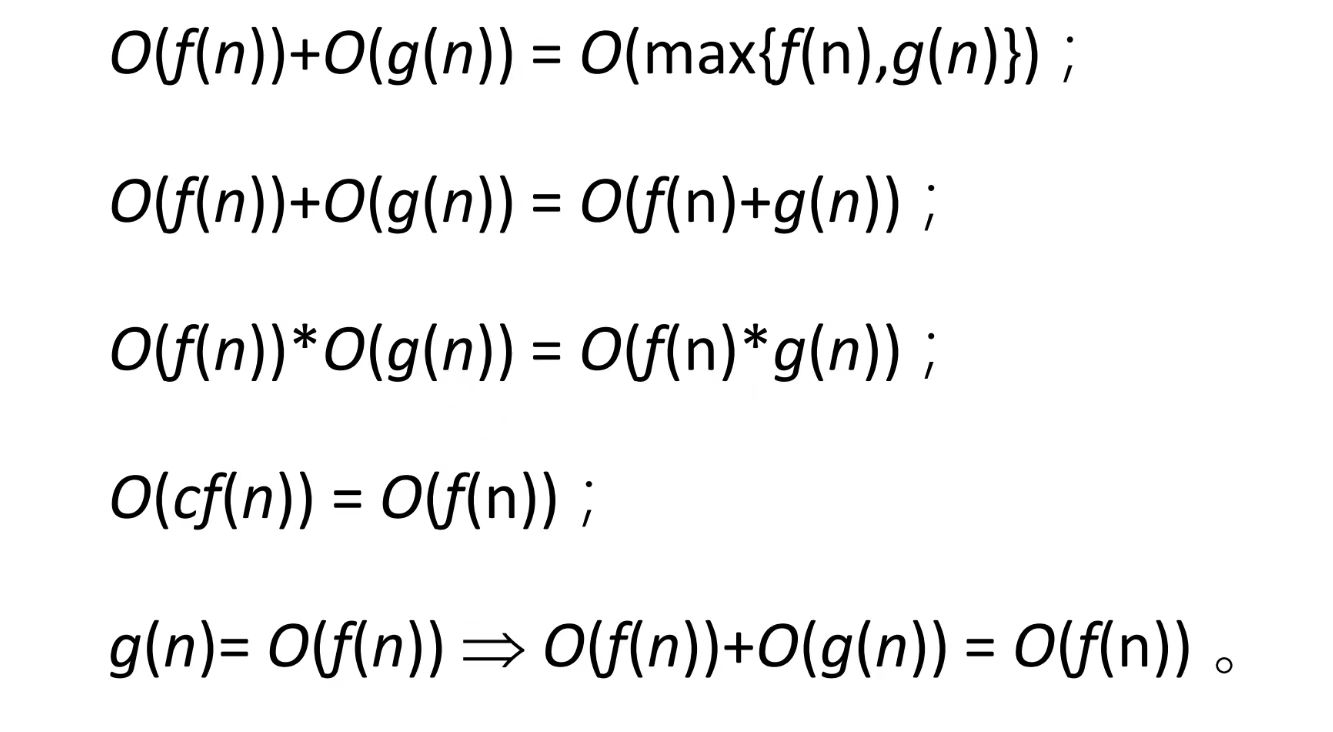
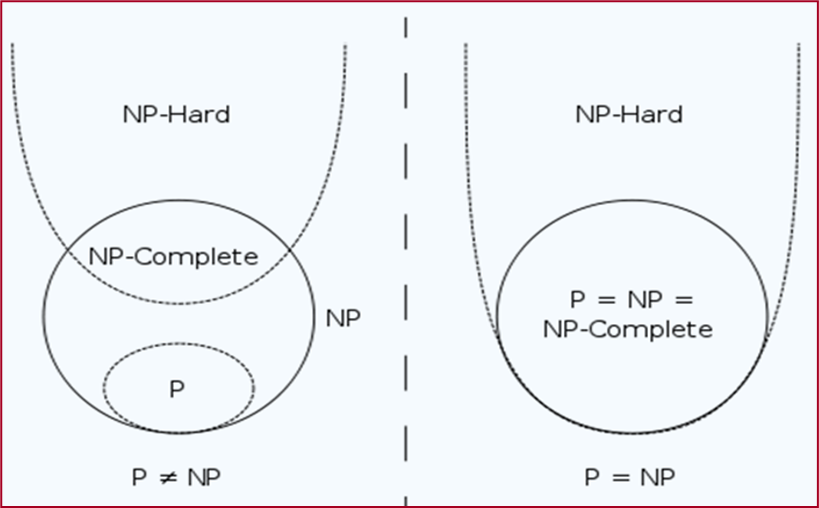
NP理论
基本定义
P:可以在多项式时间解决的问题
NP:目前没有多项式时间解决的算法,但是如果给出一个候选答案,可以在多项式时间里验证这个答案是不是正确的。
NPC:满足两个性质:
可在多项式时间验证候选答案(是NP问题);
任何一个NP问题可在多项式时间内规约到该问题。
重要性质:如果一个NP完全问题能在多项式时间内得到解决,那么NP中的每一个问题都可以在多项式时间内求解,即P=NP。
- NP-Hard:任何一个NP问题可在多项式时间内规约到该问题,但无法证明问题本身是NP问题。NP-Hard至少和NP问题一样难。