算数逻辑单元(ALU)
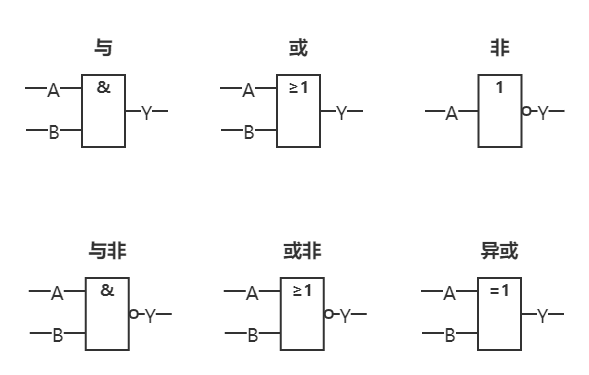
串行加法器和并行加法器
一位全加器
并行加法器
串行进位的并行加法器
把n个全加器串接起来,就可进行两个n位数的相加。
并行进位的并行加法器
补码加/减法运算器
加法器原理
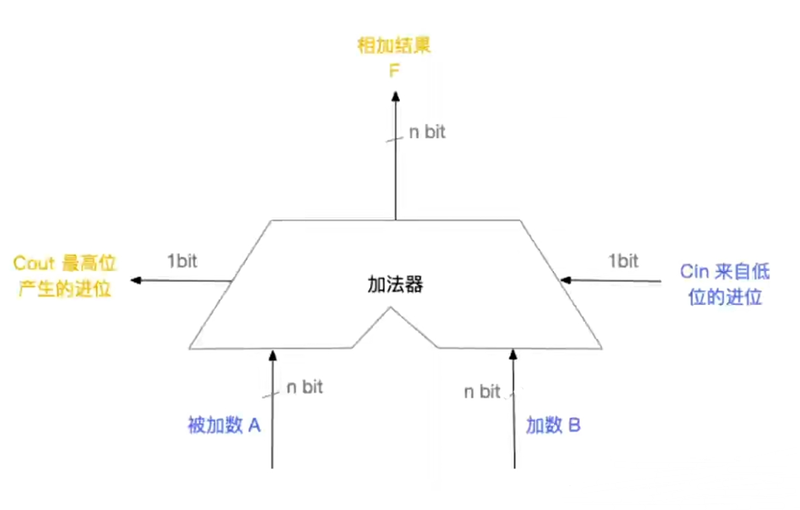
例1:A=1000,B=0111,Cin=0
则:F=1111,Cout=0
例2:A=1000,B=0111,Cin=1
则:F=0000,Cout=1
补码加减器
补码加减法原理:
X+Y:直接按位相加
X-Y:
Y全部按位取反,末位+1
减法变加法
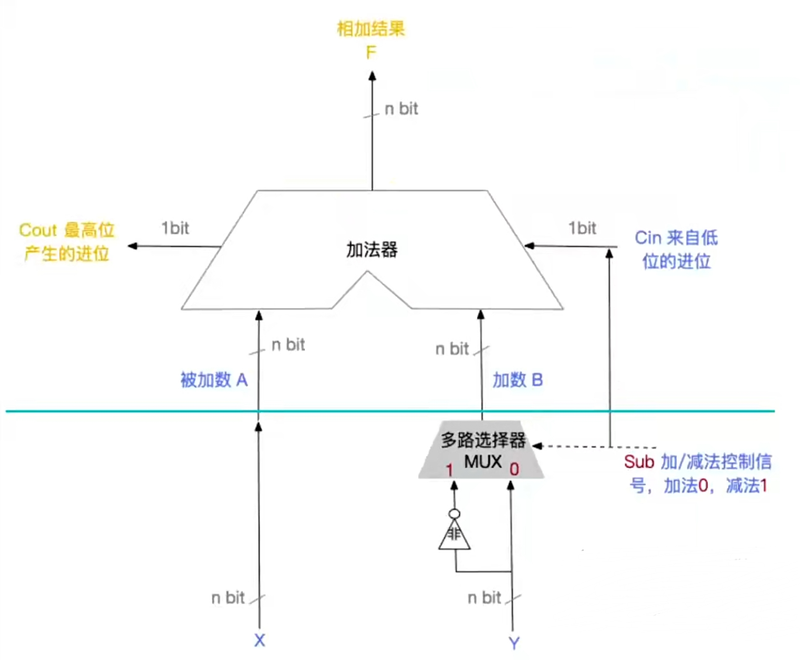
Sub信号的作用
控制多路选择器的输出
若计算减法时,1同时输入到Cin,用作补码取反后的+1
例:4bit补码,X=-8,Y=7
\(\text{X}*{补} = 1000\),\(\text{Y}*{补} = 0111\)
X+Y:直接输出:1111B(补)=-1D
X-Y:1000+(1000+1)=0001B(补)(产生溢出)
这一电路同样适用于无符号数的加减法,原理完全一致,但是判断溢出标准不同
计算机中是不会判断什么有符号无符号数,它设计出的硬件都是按0/1做运算,是人都结果做出了不同的解释
标志位
有符号数
OF:溢出标志位
最高位产生的进位与次高位产生的进位异或
判断有符号数的溢出,对无符号数没有意义
SF:符号标志位
- 取运算结果的最高位
例:4bit补码,X=-8,Y=7
X补=1000,Y补=0111
X+Y
直接输出:1111B(补)=-1D
OF=0 ⊕ 0=0:没有溢出
SF=1:结果是负数
X-Y
1000+(1000+1)=0001B
OF=1 ⊕ 0=1:产生了溢出
SF=0:结果是正数
无符号数
ZF:零标志位
- 运算结果全部为零
CF:进位标志
最高位的进位信号与sub进行异或
为1代表发生了借位,产生溢出
判断无符号数的溢出
例:4bit原码,无符号数X=3,Y=4
X=0011B,Y=0100B
X+Y
直接输出:0111B(原)=7D
ZF:0
CF:0 ⊕ 0=0
X-Y
0011+(1011+1)=1111B(原)
ZF:0
CF:0 ⊕ 1=1(产生了借位溢出)