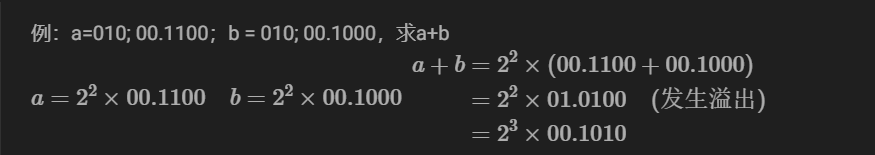前置知识
大端存储与小端存储
实际有效字节

大端存储
低地址存储最高有效字节,高地址存储最低有效字节

小端存储
与大端相反,方便机器是因为机器从低往高读

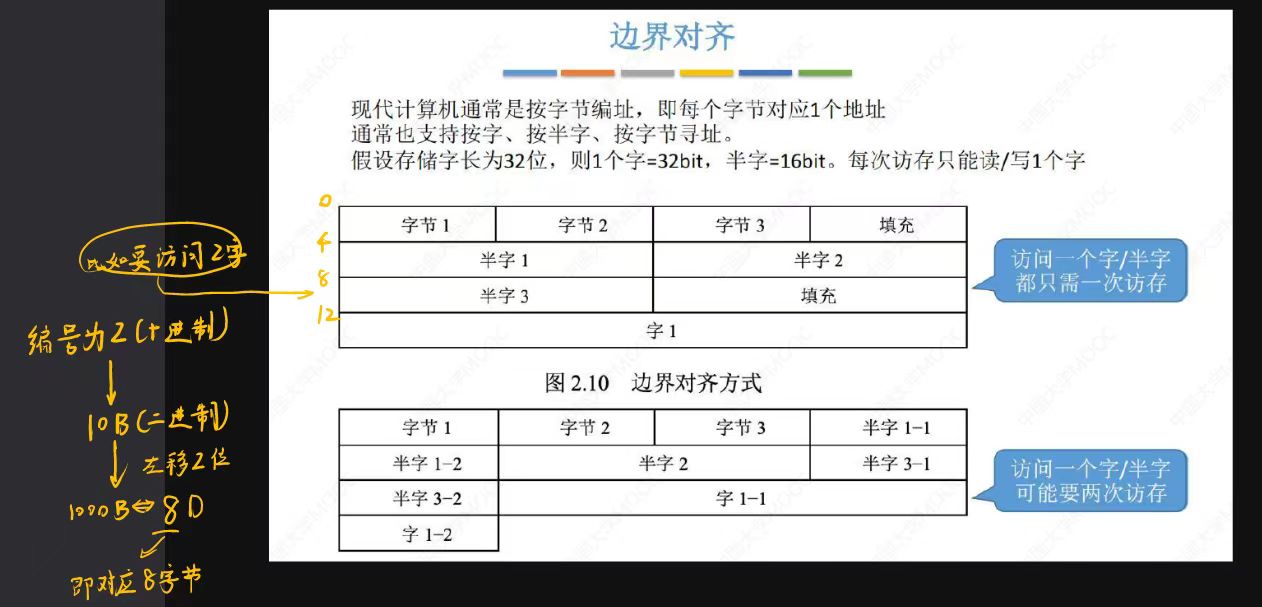
边界对齐
如何将字地址转换成与之对应的字节地址
已知字编号,对应的字节编号就是自编号逻辑左移2位
已知半字编号,对应的字节编号就是半字编号逻辑左移1位
浮点数的表示
浮点数的表示
浮点数通常表示为:
$ N = r^E * M$
- r:阶码的底,通常为2
- E:阶码,反映浮点数的表示范围和小数点的实际位置,用补码或移码表示
- M:尾数,其位数反映了小数的精度,用原码或补码表示
例:阶码和尾数都用补码表示,求a、b的真值
- a = 0,01; 1.1001
- b = 0,01; 0.01001
a:
- 阶码0,01对应真值+1
- 尾数1.1001(补码)对应真值(先转换成原码)-0.0111
- 故 a=-0.111(B)(上面二进制小数点右移1位) = \(-\frac{7}{8}\)
b:
- 阶码对应真值+1
- 尾数0.01001对应真值+0.01001
- 故 b=0.1001=\(\frac{9}{16}\)
浮点数的规格化
规格化的种类
左规
当浮点数运算的结果为非规格化时要进行规格化处理,将尾数左移一位,阶码减1 ( 基数为2时):
规定尾数的最高位必须是一个有效值。个人理解,浮点数尾数还是定点小数,表示成0.*******(正数)或者1.******(表示负数),所以符号位后,小数点下一位,也就是第二位不能是0
举例:

右规
当浮点数运算的结果尾数出现溢出(双符号位为01或10)时,将尾数右移一位,阶码加1 (基数为2时)
规格化数的特点
如何判断需要规格化
1. 无论正数负数,原码尾数最高位(就是符号位下一位)必须是1
2. 补码尾数最高位(就是符号位下一位)必须和尾数符号相反,比如正数就是1,负数就是0
举例:

规格化的小数所能表示范围
原码

补码

上溢和下溢
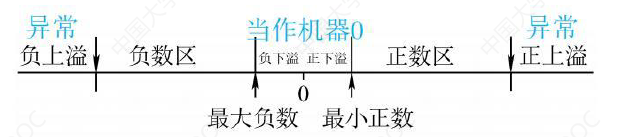
举例:

IEEE754 标准
移码的求法
移码的求法:移码 = 真值 + 偏置值
偏置值常见两种取法,一种取常数 \(2^{n - 1}\),等价于符号位取反
另一种是\(2^{n - 1} - 1,等价于加01111111(一个0和7个1)\)
举例:

注:移码只能表示整数,不能表示小数,所以移码用来表示阶码,因为阶码一定是整数
IEEE754标准下的浮点数表示
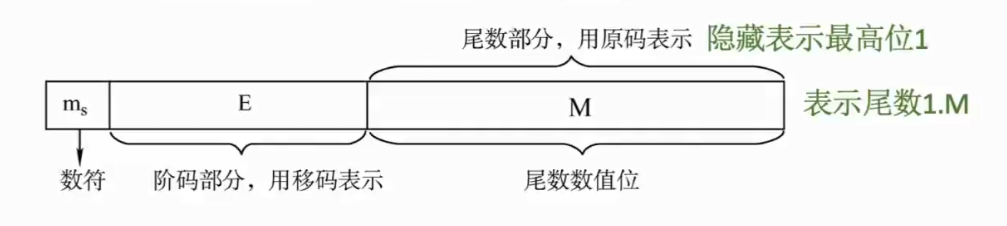
尾数前隐含一位1
| 类型 | 数阶 | 阶码 | 尾数数值 | 总位数 | 偏置值 |
|---|---|---|---|---|---|
| 短浮点数 | 1 | 8 | 23 | 32 | 7FH(127) |
| 长浮点数 | 1 | 11 | 52 | 64 | 3FFH(1023) |
| 临时浮点数 | 1 | 15 | 64 | 80 | 3FFFH |
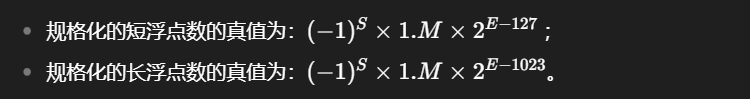
对于短浮点数而言,偏置值取127,此时阶码(移码)的表示范围为-126~127:
| 真值 | 补码 | 移码 |
|---|---|---|
| -128 | 1000 0000 | 1111 1111 |
| -127 | 1000 0001 | 0000 0000 |
| -126 | 1000 0010 | 0000 0001 |
| …… | …… | …… |
| 0 | 0000 0000 | 0111 1111 |
| …… | …… | …… |
| 127 | 0111 1111 | 1111 1110 |
-128和-127的作用:
E=0且 M=0,则真值为0;
E=0且 E≠0 M≠0,为非规格化数,真值 = (-1)^S ×0.M×2^(-126);
E=255且 E≠0 M≠0,真值为‘NaN’(非数值);
E=255且 E=0 M=0,真值为正或负无穷。
例1:十进制小数转单精度浮点数

例2:单精度浮点数转十进制

浮点数的运算
加减运算
步骤:
对阶
尾数加减
规格化
舍入
判溢出
已知十进制数: \(X = -\frac{5}{256}\) \(Y = +\frac{59}{1024}\)
按机器补码浮点运算规则计算 ( X - Y ),结果用二进制表示,浮点数格式如下:阶符取2位,阶码取3位,数符取2位,尾数取9位。 例子中的浮点数计算过程如下:
- 计算X和Y的浮点表示:
X: 阶码: -101(补码为:1011,阶符取两位、阶码取三位:11011) 尾数: -0.101(补码为1.011,数符取两位、尾数取九位:11.011000000)
Y: 阶码: -100(补码为1100,阶符取两位、阶码取三位:11100) 尾数: +0.111011(补码为0.111011,数符取两位、尾数取九位:00.111011000)
对阶: 计算阶码差:ΔE = 11011 - 11100 = 11011 + 00100 = 11111 (11111为-1的补码) 所以 ΔE = -1 ,X的阶码比Y的阶码小1 阶码每加1,尾数右移一位,则有新的X:11100;11.101100000(右移之后前面补1)
尾数相加减: -Y: 11100;11.000101000 尾数相加,得:10.110001000
规格化: 尾数右移一位,阶码加1,得:X-Y=11101;11.011000100
舍入: 由于无舍入,不需要进行舍入操作。
判断溢出: 未发生溢出
因此,结果真值为 \(2^{-3} \times (-0.1001111)_2\)。
强制类型转换
| 数据类型 | 16位机器 | 32位机器 | 64位机器 |
|---|---|---|---|
| char | 8 | 8 | 8 |
| short | 16 | 16 | 16 |
| int | 16 | 32 | 32 |
| long | 32 | 32 | 64 |
| long long | 64 | 64 | 64 |
| float | 16 | 32 | 32 |
| double | 64 | 64 | 64 |
char --> int --> long --> double 以及 float --> double,不会损失精度。
对于32位系统:
整数类型(int)表示整数,范围为 \(-2^{31} \sim 2^{31}-1\),有效数字32位。
浮点数类型(float)表示整数及小数,范围为 \(\pm [2^{-126} \sim 2^{127} \times (2^{-2^{-23}})]\),有效数字为23位尾数加1位整数部分,共24位。
在进行类型转换时:
int --> float:可能会损失精度,因为float类型的有效数字比int类型多。
float --> int:可能会溢出(超出int表示范围),同时可能损失精度(小数部分被舍弃)。