给定一个按照升序排列的长度为 n的整数数组,以及 q 个查询。
对于每个查询,返回一个元素 k 的起始位置和终止位置(位置从 0
开始计数)。
如果数组中不存在该元素,则返回 -1 -1。
输入格式
第一行包含整数 n和 q,表示数组长度和询问个数。
第二行包含 n 个整数(均在 1∼100001∼10000 范围内),表示完整数组。
接下来 q 行,每行包含一个整数 k ,表示一个询问元素。
输出格式
共 q 行,每行包含两个整数,表示所求元素的起始位置和终止位置。
如果数组中不存在该元素,则返回 -1 -1。
数据范围
1≤n≤1000001≤ ≤100000 1≤q≤100001≤ ≤10000 1≤k≤100001≤ ≤10000
输入样例:
输出样例:
分析
二分模板
1
2
3
4
5
6
7
8
9
10
11
12
|
static int[] data = new int[MAX];
static int void search_left(int target, int start, int end) {
int mid = 0;
while(start < end) {
int mid = (start + end) / 2;
if(check(mid)) end = mid;
else start = mid + 1;
}
return start;
}
|
这种二分是要在一个范围内,找到指定范围的最左端和最右端
以找最左端为例
check(mid)如何决定
mid的目的是将一段区间分割成两端,其中一段(包括mid)均满足check规定的性质,另一端都不满足
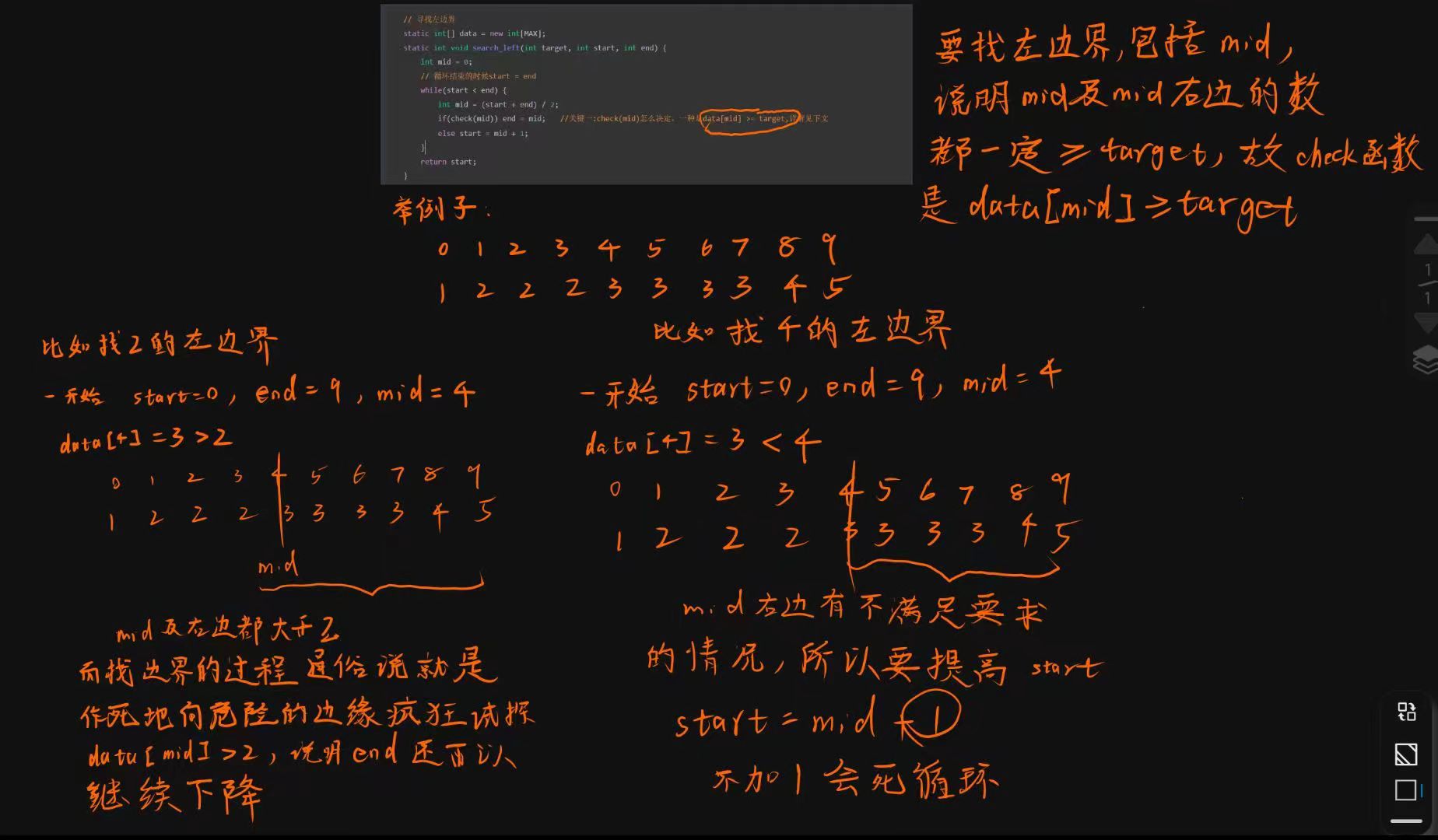
总结
决定check函数
- 一定包含mid,就是一定要有=
- 向危险的边缘疯狂试探的思想
口诀:左边界,无加必有加;有边界有加必有减
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
| import java.util.Scanner;
import javax.security.auth.kerberos.KerberosKey;
public class Main {
static int[] data = new int[100010];
static int search_left(int target, int start, int end) {
int mid = 0;
while(start < end) {
mid = (start + end) / 2;
if(data[mid] >= target) end = mid;
else start = mid + 1;
}
return start;
}
static int search_right(int target, int start, int end) {
int mid = 0;
while(start < end) {
mid = (start + end) / 2 + 1;
if(data[mid] <= target) start = mid;
else end = mid - 1;
}
return start;
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int q = scan.nextInt();
for(int i = 0; i < n; i++) {
data[i] = scan.nextInt();
}
for(int i = 0; i < q; i++) {
int target = scan.nextInt();
int leftSide = search_left(target, 0, n - 1);
if(data[leftSide] != target) {
System.out.println("-1 -1");
continue;
} else {
System.out.print(leftSide + " ");
}
int rightSide = search_right(target, 0, n - 1);
if(data[rightSide] != target) {
System.out.println("-1 -1");
} else {
System.out.println(rightSide);
}
}
scan.close();
}
}
|
举一反三
分析:
在while循环里使用stride表示left与right之间的距离,当距离足够小的时候可以近似认为相等
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
double n = scan.nextDouble();
double left = (-1.0) * 10000;
double right = 10000.0;
double stride = 1e-8;
while(right - left > stride) {
double mid = (left + right) / 2;
if(mid * mid * mid >= n) right = mid;
else left = mid + stride;
}
System.out.format("%.6f", right);
scan.close();
}
}
|
分析
二维
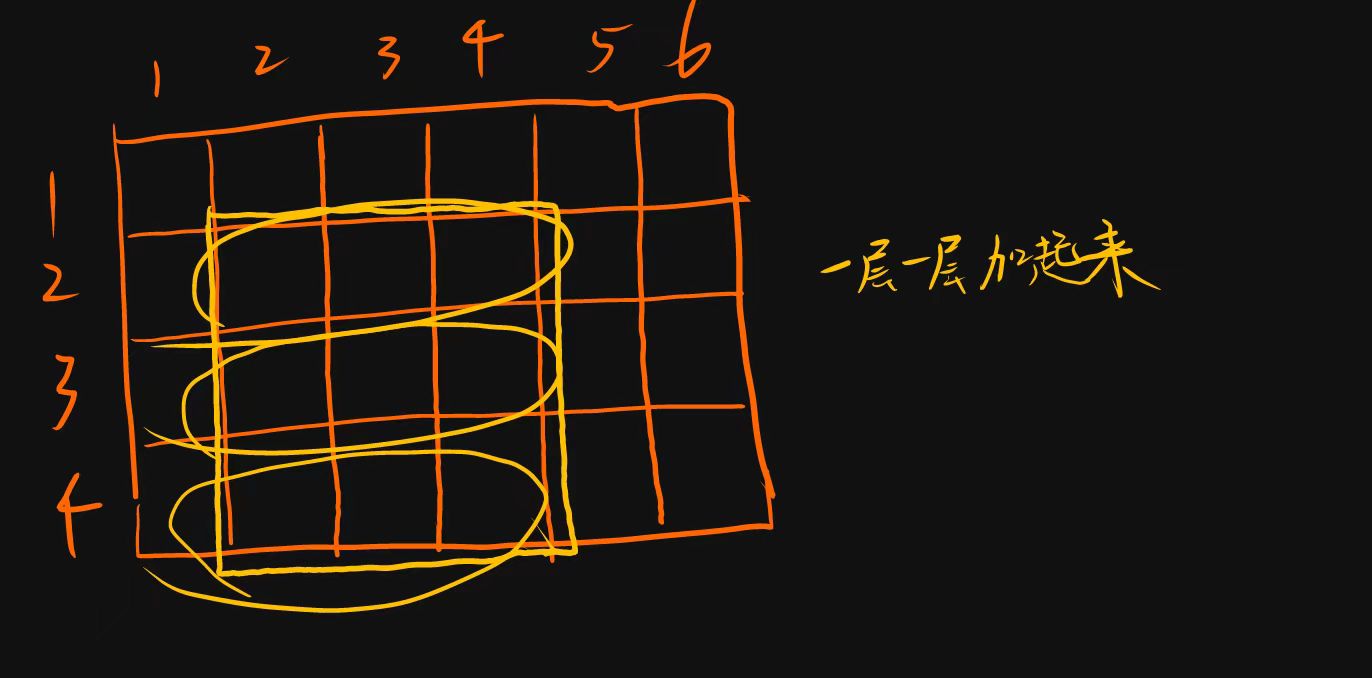
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import java.util.Scanner;
public class Main {
static int[][] data = new int[1010][1010];
static int[][] prefixSum = new int[1010][1010];
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= m; j++) {
data[i][j] = scan.nextInt();
if(i == 0) {
prefixSum[i][j] = prefixSum[i - 1][m] + data[i][j];
} else {
prefixSum[i][j] = prefixSum[i][j - 1] + data[i][j];
}
}
}
for(int i = 0; i < q; i++) {
int leftX, leftY;
leftX = scan.nextInt();
leftY = scan.nextInt();
int rightX = scan.nextInt();
int rightY = scan.nextInt();
int totalSum = 0;
for(int row = leftX; row <= rightX; row++) {
totalSum += (prefixSum[row][rightY] - prefixSum[row][leftY - 1]);
}
System.out.println(totalSum);
}
scan.close();
}
}
|

