多层感知机定义：与前面提到的softmax回归构成的全连接层相比就是增加了隐藏层

通过在网络中加入一个或多个隐藏层

最简单的方法是将许多全连接层堆叠在一起。每一层都输出到上面的层，直到生成最后的输出

这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。

举例

4个输入，3个输出

隐藏层包含5个隐藏单元。

输入层不涉及任何计算

产生输出只需要实现隐藏层和输出层的计算。

因此，这个多层感知机中的层数为2。

两个层都是全连接的。每个输入都会影响隐藏层中的每个神经元，而隐藏层中的每个神经元又会影响输出层中的每个神经元。

激活函数

定义：

在仿射变换之后对每个隐藏单元应用非线性的激活函数（activation function）\(\sigma\)，防止多层感知机退化成线性模型

大多数激活函数都是非线性的

作用：

过计算加权和并加上偏置来确定神经元是否应该被激活

种类

ReLU函数

当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。

输入值精确等于0时，ReLU函数不可导。在此时，我们默认使用左侧的导数，即当输入为0时导数为0

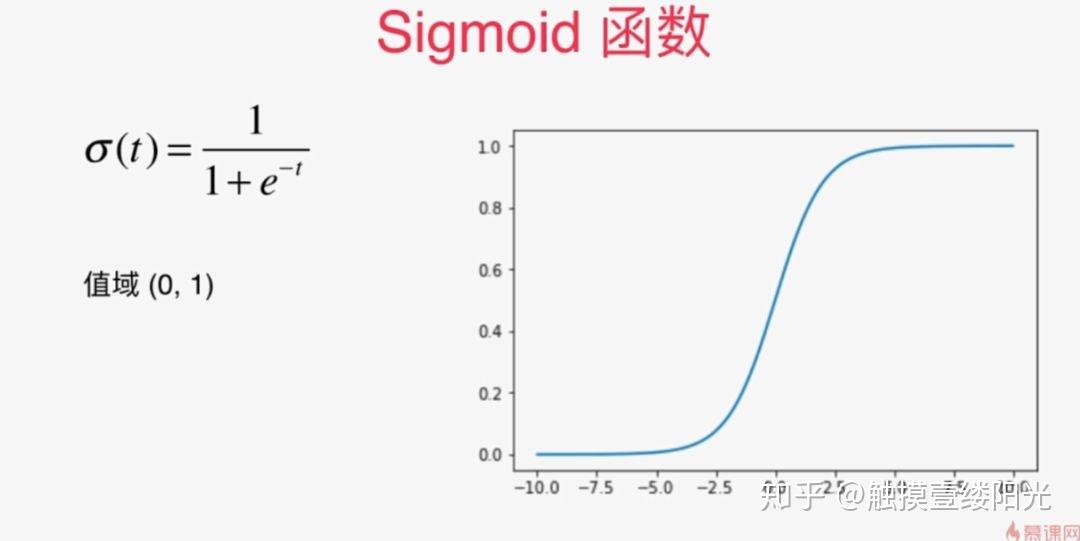
sigmoid函数

实现

初始化模型参数

每个图像由 28×28=784个灰度像素值组成。所有图像共分为10个类别。忽略像素之间的空间结构，我们可以将每个图像视为具有784个输入特征和10个类的简单分类数据集

实现一个具有单隐藏层的多层感知机，它包含256个隐藏单元

可以将这两个变量都视为超参数。通常，我们选择2的若干次幂作为层的宽度

对于每一层我们都要记录一个权重矩阵和一个偏置向量

激活函数RELU

模型

net = nn.Sequential(nn.Flatten(),
                    nn.Linear(784, 256),
                    nn.ReLU(),
                    nn.Linear(256, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

Pilot's Blog

多层感知机