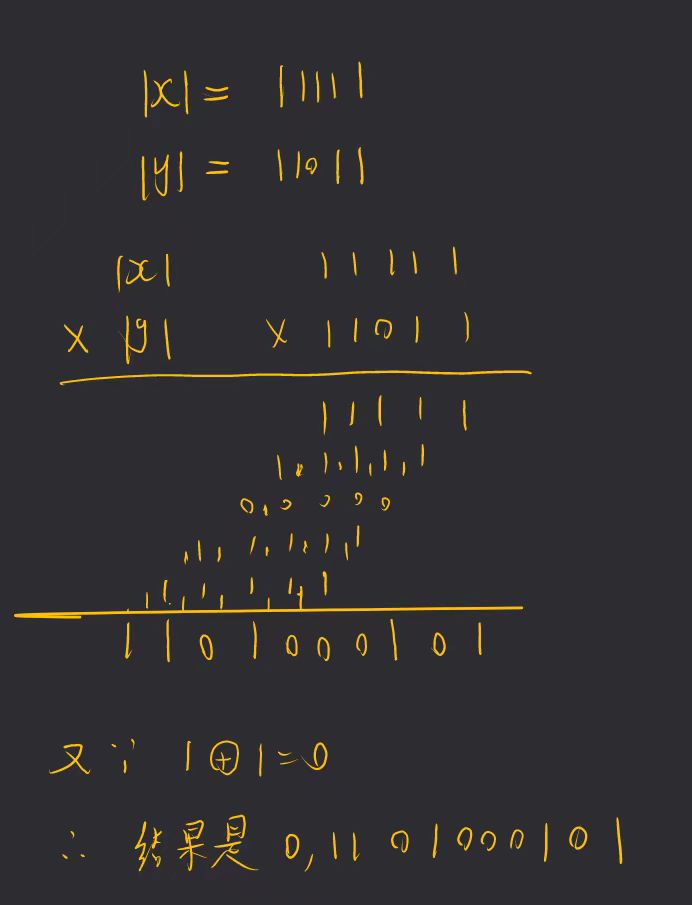定义
行波进位与先行进位

解析:
行波进位表示只能像平时手工计算一样算出一位再算下一位,先行进位就是通过设计使得能够同时计算出多个位。其中一片74181ALU能在组内实现先行进位,多片74181ALU在74182CLA帮助下能实现组间行波进位
双符号位

- 第一符号位表示运算结果符号
- 如果运算结果两符号位不同,则表明产生了溢出。“10”表示负溢出(下溢出),说明运算结果为负数,“01”表示正溢出(上溢出),说明运算结果为正数
尾数规格化

解析:
就是这么设计的,记住就行
计算题
原码、反码、补码
- 原码的第一位一定是符号位
- 反码是原码的符号位不变,其他取反
- 补码是反码加1,或者原码符号位不变,其他取反后加1
浮点数最值


关于补码最小值的解释:
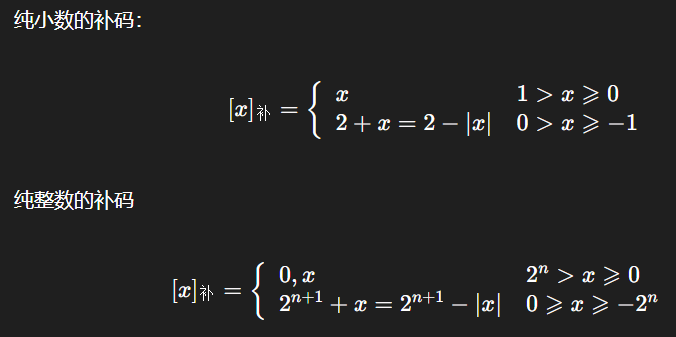

上面其实是补码设计,补码来源于一个数加它的相反数结果是0,然后为了方便借位加了1
升级版,不仅要求,还要能表示,设计移码和补码


注:非IEEE754不需要的移码的偏置值不需要减1,就是\(2^{n-1}\)就行
IEEE754
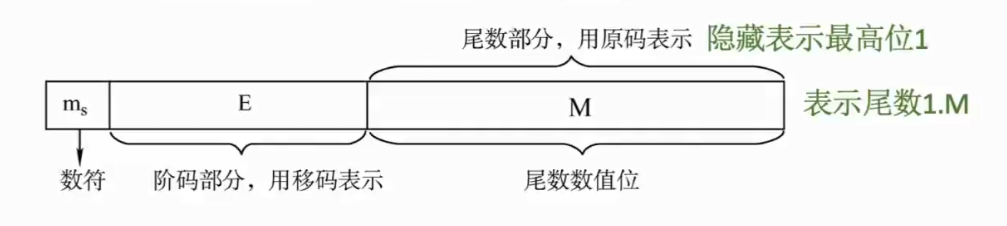
- 尾数用原码表示,隐藏表示最高位1,表示为1.M,一共23位
- 阶码用移码表示,表示的是整数,相对于补码加了01111111B(127D),一共有8位
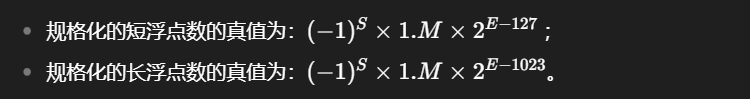
十进制数转二进制浮点数

- 转为二进制科学计数法所表示的数,注意是\(1.M * 2^k\)的一个形式,不要忘记整数1!!!
- 然后确定符号,将k+127作为阶码,将M作为尾数
十六进制浮点数转十进制小数

- 转换为二进制
- 根据第一位符号位确定正负
- 取阶码,将阶码当做无符号整数减127(二进制01111111)得到真值
- 剩下作为尾数小数点之后的数M,尾数实际上是1.M
定点数的除法运算
由于定点小数绝对值<1,因此,在定点机器中,进行除法运算之前,必须先判断结果是否会溢出,即判断|被除数|是否大于或者等于 |除数| 。
原码恢复余数法
- 先求出被除数x的绝对值的补码\([|x|]_{补}\),再求出除数y的绝对值的补码\([|y|]_{补}\)和除数y的绝对值的相反数的补码\([-|y|]_{补}\)
- 每次先商1,加\([-|y|]_{补}\),如果结果小于0(这里的结果就是余数小于0),那修改商为0并且加上\([|y|]_{补}\)
- 将得到的余数左移1位,从第2步开始循环
- 最终计算得到的商的位数和被除数位数一样
原码加减交替法
- 先求出被除数x的绝对值的补码\([|x|]_{补}\),再求出除数y的绝对值的补码\([|y|]_{补}\)和除数y的绝对值的相反数的补码\([-|y|]_{补}\)
- 每次先商1,加\([-|y|]_{补}\),如果余数是负的,就左移商0下一步加正的\([|y|]_{补}\);如果余数是正的,就左移商1下一步加负的\([-|y|]_{补}\),重复第2步
- 最终计算得到的商的位数和被除数位数一样
浮点数的加减计算
- 判断当前操作数是否为0
- 対阶,小阶向大阶对齐
- 尾数规格化,尾数一定要是0.0或者1.0,不是的就要规格化尾数同时修改阶码
- 判断是否溢出


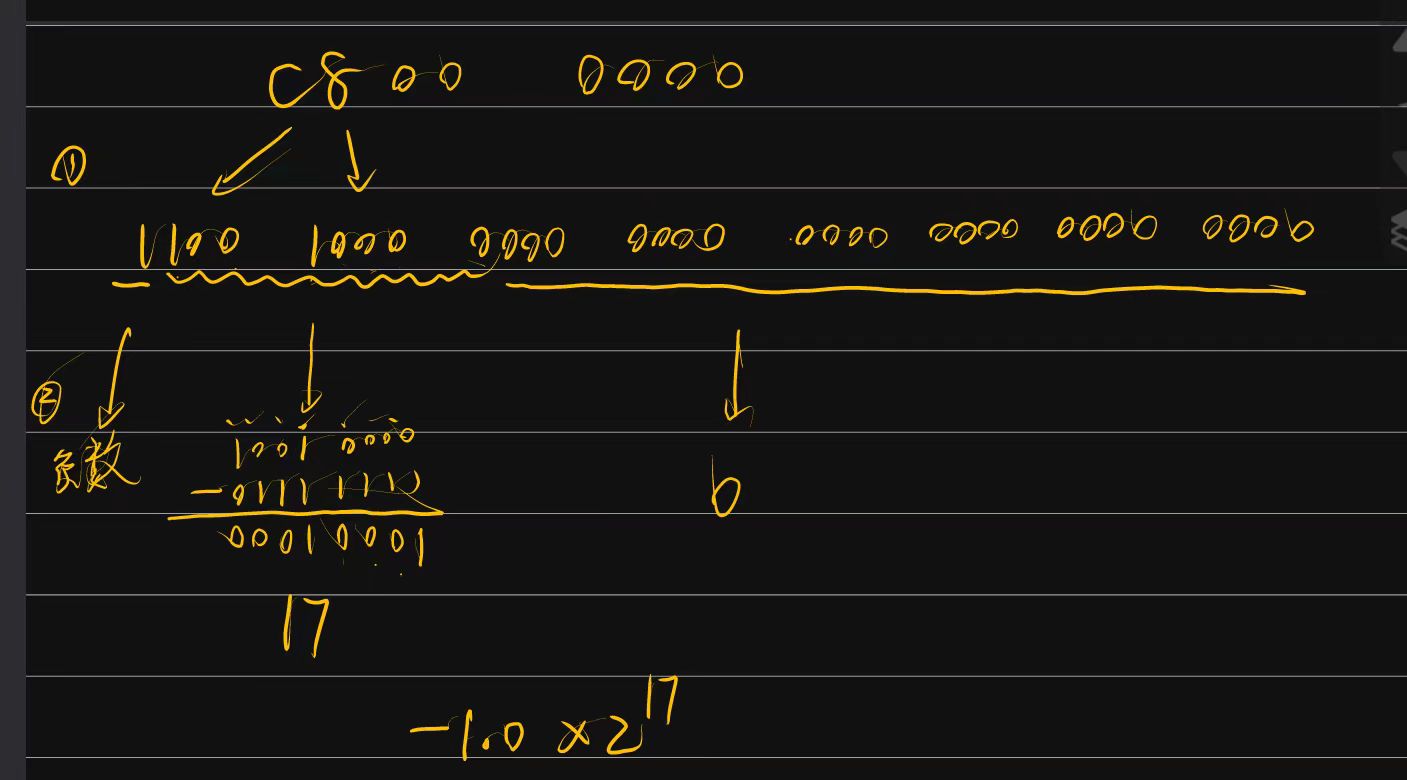
注:上面快速求二进制小数的技巧
溢出的判断


注:如何快速得到一个负数补码的真值的技巧见上
乘法
比如计算x = -11111, y = -11011