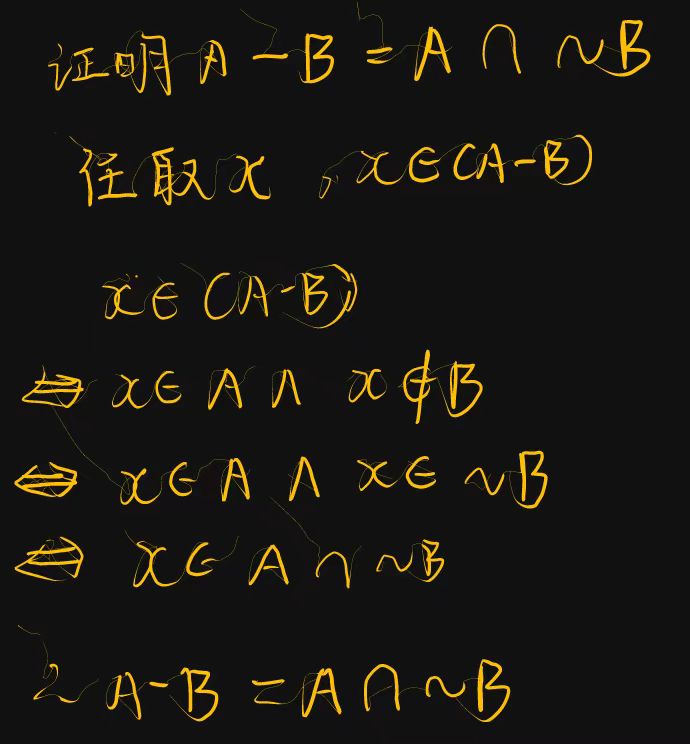集合的基本概念
集合表示法中微词表示法举例:\(S = \{x|x是实数且x^2 - 1 = 0\}\)
元素与集合
性质
无序性:元素列出的顺序无关
相异性:集合的每个元素只计数一次
确定性:对任何元素和集合都能确定这个元素是否为该集合的元素
任意性:集合的元素也可以是集合
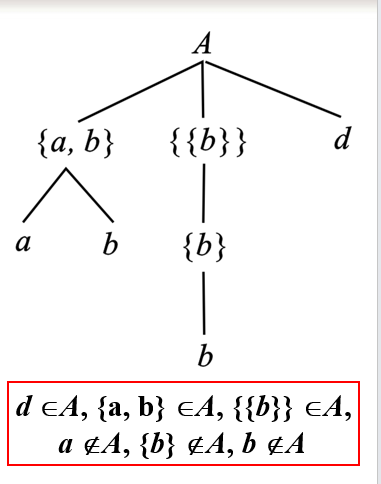
从上图来看,集合中元素属于这个集合必须是直接属于
集合与集合
定义6.1子集:\(A \subseteq B \Leftrightarrow \forall x (x \in A \rightarrow x \in B\)
定义6.1非子集:\(A \nsubseteq B \Leftrightarrow \exists x (x \in A \land x \notin B)\)
定义6.2相等:\(A = B \Leftrightarrow A \subseteq B \land B \subseteq A\)
定义6.3真子集:\(A \subsetneq B \Leftrightarrow A \subseteq B \land A \neq B\)
注意: \(\in\)和\(\subseteq\)是不同层次的问题,其中:
- \(\in\)可以看作是不同层次上的集合元素与集合之间的关系。通俗点说就是{ }数量不等
- \(\subseteq\)是同一层次上的两个集合之间的关系。通俗点说就是{ }数量相等
空集、全集和幂集
幂集:集合A的全体子集构成的集合,记作\(P(A) = \{ x \, | \, x \subseteq A \}\)
实例:
\(P(\emptyset) = \{\emptyset\}, P(\{\emptyset\}) = \{\emptyset, \{\emptyset\}\}\)
第二个例子就是把空集当成1个普通元素就行,同时注意集合包含关系要求{ }层数相等
计数:如果\(|A| = n ,则 |P(A)| = 2^n\)
集合的基本运算
初级运算
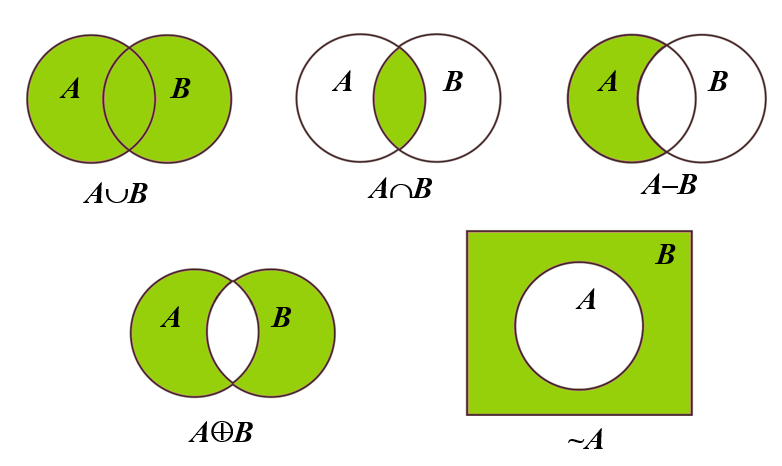
并:\(A \cup B = \{x \, | \, x \in A \lor x \in B\}\)
交:\(A \cap B = \{x \, | \, x \in A \land x \in B\}\)
相对补:\(A - B = \{x \, | \, x \in A \land x \notin B\}\)
对称差:\(A \oplus B = (A - B) \cup (B - A)\)
绝对补:\(\sim A = E - A\)
广义运算
集合的广义并与广义交
广义并:集合A的元素的元素构成的集合,记作\(\bigcup A = \{ x \, | \, \exists z (z \in A \land x \in z) \}\)
广义交:非空集合A的所有元素的公共元素构成的集合,记作\(\bigcap A = \{ x \, | \, \forall z (z \in A \rightarrow x \in z) \}\)

性质
- \(\bigcup \emptyset = \emptyset , \bigcap \emptyset\)无意义
- 单元集\(\{x\}\)的广义并和广义交都等于\(x\)
- 广义运算减少集合的层次(括弧减少一层)
- 广义运算的计算:一般情况下可以转变成初级运算
运算的优先权规定
类运算:初级运算\(\cup , \cap , - , \oplus\), 优先顺序由括号确定。
类运算:广义运算和\(\sim\)运算, 运算由右向左进行。
混合运算:2 类运算优先于 1 类运算。
举例:
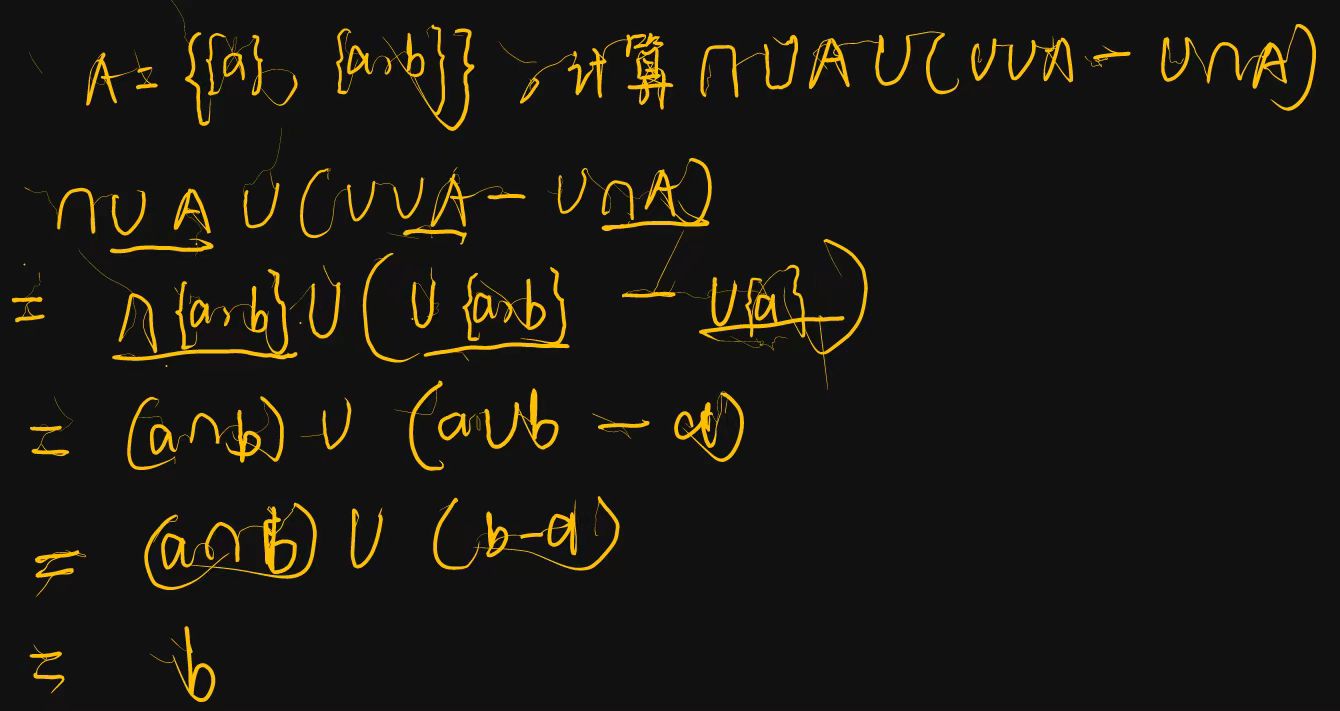
有穷集的计数
容斥原理
(多个字母的并事件):奇数个字母前面是正号,偶数个字母前面是负号,然后组合排列出所有情况


举例:
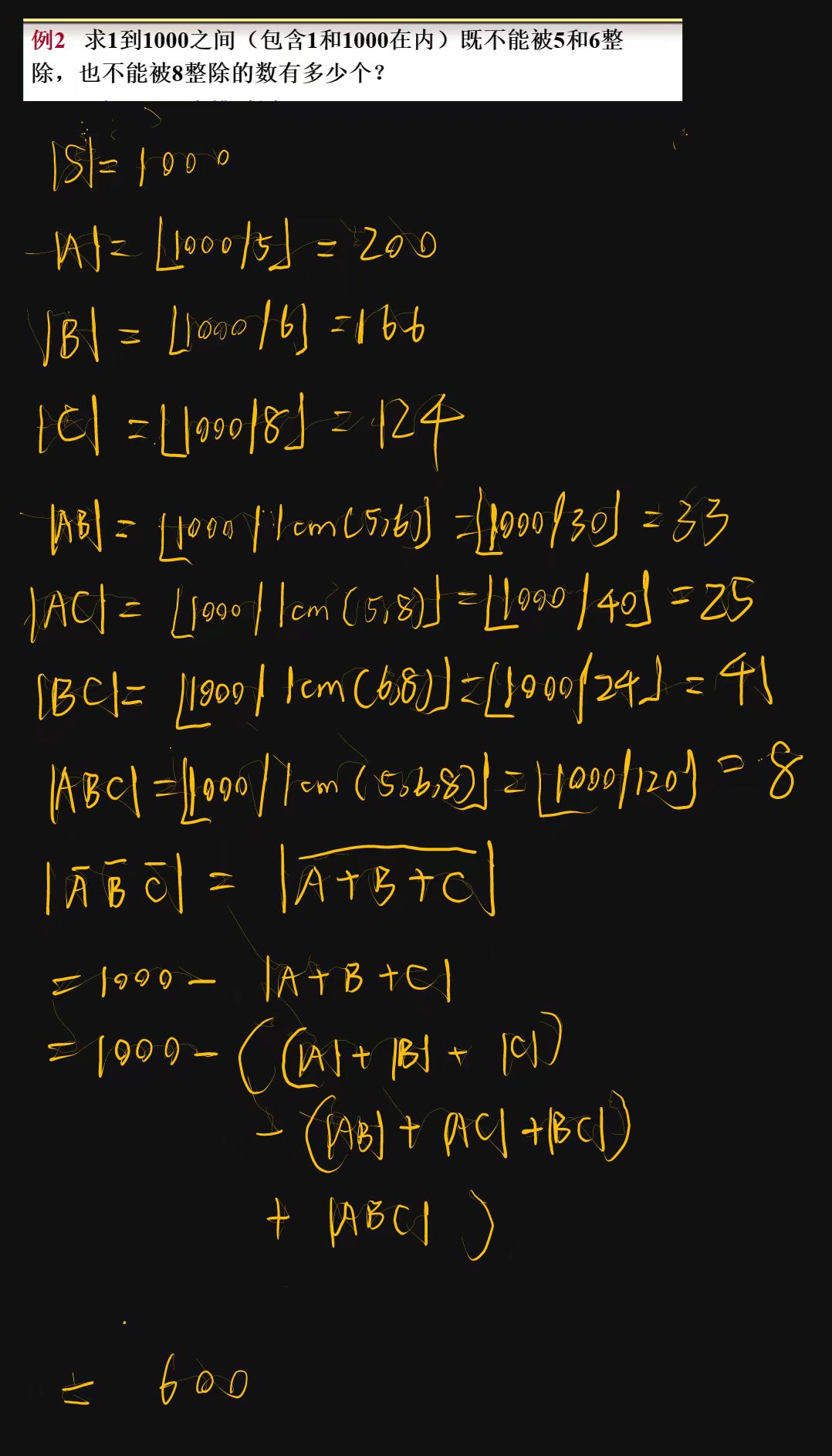
集合恒等式
只涉及一个运算的算律
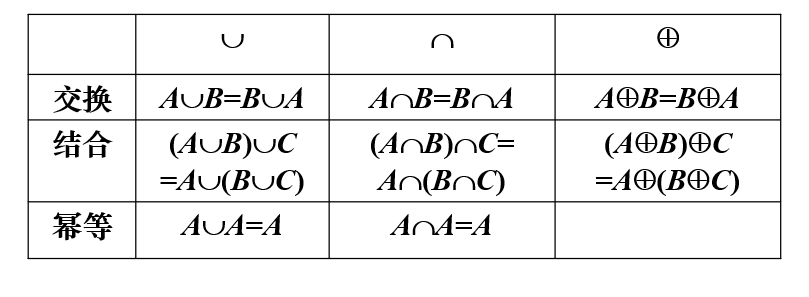
涉及两个不同运算的算律

涉及补运算的算律
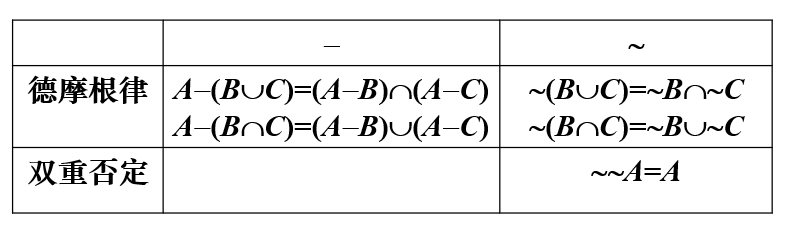
涉及全集和空集的算律

集合证明题
证\(X \subseteq Y\) 任取\(x\),\(x \in X \Rightarrow \ldots \Rightarrow x \in Y\)
证\(X = Y\) 方法一:分别证明\(X \subseteq Y\)和\(Y \subseteq X\) 方法二:任取\(x\),\(x \in X \Leftrightarrow \ldots \Leftrightarrow x \in Y\)
集合等式的证明
举例: