进位计数法
基数:每个数位所要用到的不同符号的个数(二进制就是2个、8进制就是8个、十进制就是10个...)。
基数越大,位数越小,运算情况越多。
位权:依据进制所决定的一个常数(二级制就是2,十进制就是10...)
N位r进制的数所能表示的数字个数为:\(r^N\)个
进制转换
(一)、任意进制 --> 十进制
用相应位上的数乘以位权即可。
二进制:101.1 --> \(1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0 + 1 \times 2^{-1} = 5.5\)
八进制:5.4 --> \(5 \times 8^0 + 4 \times 8^{-1} = 5.5\)
十六进制:5.8 --> \(5 \times 16^0 + 8 \times 16^{-1} = 5.5\)
(二)、十进制 --> 任意进制
例:将十进制123.6875转化为二进制
除基取余法(整数)
对整数部分的处理使用短除法,并从下向上,得1111011
.png)
乘基取整法(小数)
小数部分采用乘基取整的思路,如下所示:

一般十进制无法精确化为二进制小数,取一定精度即可。
(二)、 \(2^n\) 进制之间的转换
每n位一组,进行对应的转换即可。
例1:将3C2.68H转化为二进制
3C2.68H = 1111000010.01101B
例2:将1111000010.01101B转化为八进制
1111000010.01101B = (1702.32)8
BCD码
BCD(Binary-Coded Decimal),使用二进制表示的十进制数。即使用四位二进制数表示一位十进制数,使得十进制与二进制之间的转换得以快速进行。
8421码
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 |
使用8421码进行运算时,若结果大于等于10,需要加6修正(加0110)
举例:
余三码
将8421码的每一位加3(即加0011B)得到。
2421码
将最高位的权值改为2,特点是大于5的四位二进制码最高位是1,小于5的是0.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 0000 | 0001 | 0010 | 0011 | 0100 | 1011 | 1100 | 1101 | 1110 | 1111 |
字符与字符串
ASCII码
- 32~126位称为可印刷字符
- A-Z,a-z是连续的,但是Z和a之间不连续
- 以字节的形式存储
例:已知'A'的ASCII码码值是65,H存放在某存储单元M中,求M中存放的值
65+(8-1)=72
72 = 0100 1000
字符串
字符串:IF A>B THEN READ(C) ,每个存储单元存放4B
大端模式:存储单元内先存储高位字节、后存储低位字节的顺序
大端方式是正常的
| I | F | 空格 | A |
|---|---|---|---|
| > | B | 空格 | T |
| H | E | N | 空格 |
| R | E | A | D |
| ( | C | ) | 空格 |
小端模式:存储单元内先存储低位字节、后存储高位字节的顺序
| A | 空格 | F | I |
|---|---|---|---|
| T | 空格 | B | > |
| 空格 | N | E | H |
| D | A | E | R |
| 空格 | ) | C | ( |
汉字编码
包括输入的输入编码,计算机内部处理的汉字内码和输出的汉字字形码三种。
.png)
校验码
码距:任意两个合法码字之间不同的二进制的位数。
- 码距大于等于2时,开始具有检错能力
- 码距越大,纠错、检错能力越强
奇偶校验码
添加一个校验位,校验位的取值满足以下规定:
奇校验:这串序列1的个数如果为偶数则在前面加个1,使1的个数变成奇数,否则加0。将1的个数凑成偶数
偶校验:这串序列1的个数如果为奇数则在前面加个1,使1的个数变成偶数,否则加0。将1的个数凑成奇数
举例: 1111 奇校验就是 11111 偶校验就是 01111 1110 奇校验就是 01110 偶校验就是 11110
特性是检测一位错,无法纠错。
海明校验码
循环冗余校验码
循环冗余校验码包括K位数据位和R位校验位。
例:已知生成多项式\(G(x) = x^3 + x^2 + 1\) ,信息码为101001,求对应的CRC码
确定K、R及生成多项式对应的二进制码
K = 7
R = 生成多项式的最高次幂 = 3
则,CRC码的位数 = K + R = 10
生成多项式的各次幂的系数就是对应的二进制码:1101(没有x,故第二位为0)
移位
将信息码左移R位,低位补0
101001000
模2相除
将左移后的信息码除以生成多项式的二进制码。
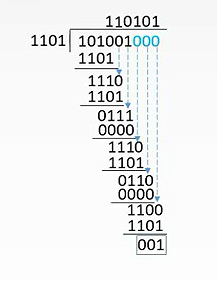
二进制除法是两两异或,不是相减!
最后的余数就是校验位
因此,CRC码 = 101001 001
4、检错
对于CRC码再次用生成多项式的二进制码进行模2除法,余数应为000。