Pilot's Blog
0%

DP动态规划入门

发表于 更新于 分类于 ， ， Valine：
本文字数： 3.2k 阅读时长 ≈ 3 分钟

基本概念

核心思想

为了解决一个“大”问题，将“大”问题分解成两个“小”问题

举个例子：一次可以走一个台阶或者两个台阶，问走到第n个台阶时，一共有多少种走法？要走到第n级台阶，分成两种情况，一种是从n-1级台阶走一步过来，一种是从n-2级台阶走两步过来

状态

形如dp[i][j] = val的取值，其中i, j为下标，用于描述、确定状态所需的变量，val为状态值

状态转移

状态与状态之间的转移关系，转移方向决定了迭代或递归方向

常见特征：重叠子问题，最优子结构

重叠子问题：

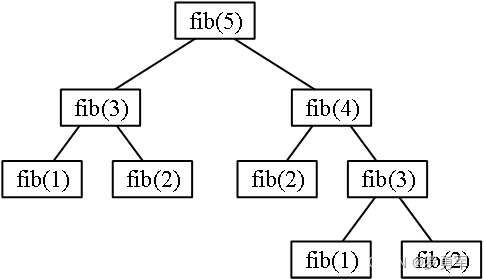
斐波那契数为例，用递归计算fib(5)，分解为图示的子问题，其中fib(3)计算了2次，其实只算1次就够了

最优子结构

两种编码方法

自顶向下与记忆化

先考虑大问题，再缩小到小问题，递归很直接地体现了这种思路。为避免递归时重复计算子问题，可以在子问题得到解决时，就保存结果，再次需要这个结果时，直接返回保存的结果就行了。这种存储已经解决的子问题的结果的技术称为“记忆化（Memoization）”。   以斐波那契数为例，记忆化代码如下：

1
2
3
4
5
6
7
int memoize[N];                                  //保存结果
int fib (int n){
    if (n == 1 || n == 2)  return 1;
    if(memoize[n] != 0) return memoize[n]; //直接返回保存的结果，不再递归
    memoize[n]= fib (n - 1) + fib (n - 2);       //递归计算结果，并记忆
    return memoize[n];
}

自下而上与制表递推

先解决子问题，再递推到大问题。通常通过填写表格来完成，编码时用若干for循环语句填表。根据表中的结果，逐步计算出大问题的解决方案。

用制表法计算斐波那契数，维护一个一维表dp[]，记录自下而上的计算结果，更大的数是前面两个数的和。

1
2
3
4
5
6
7
const int N = 255;
int dp[N];
int fib (int n){
    dp[1] = dp[2] =1;
    for (int i=3;i<=n;i++)  dp[i] = dp[i-1] +dp[i-2];
    return dp[n];
}

分析步骤

确定状态

一般为“到第i个为止，方案数/最小代价/最大价值

确定状态转移方程

根据状态转移方向决定迭代还是递归

确定最终状态

题目一

题干

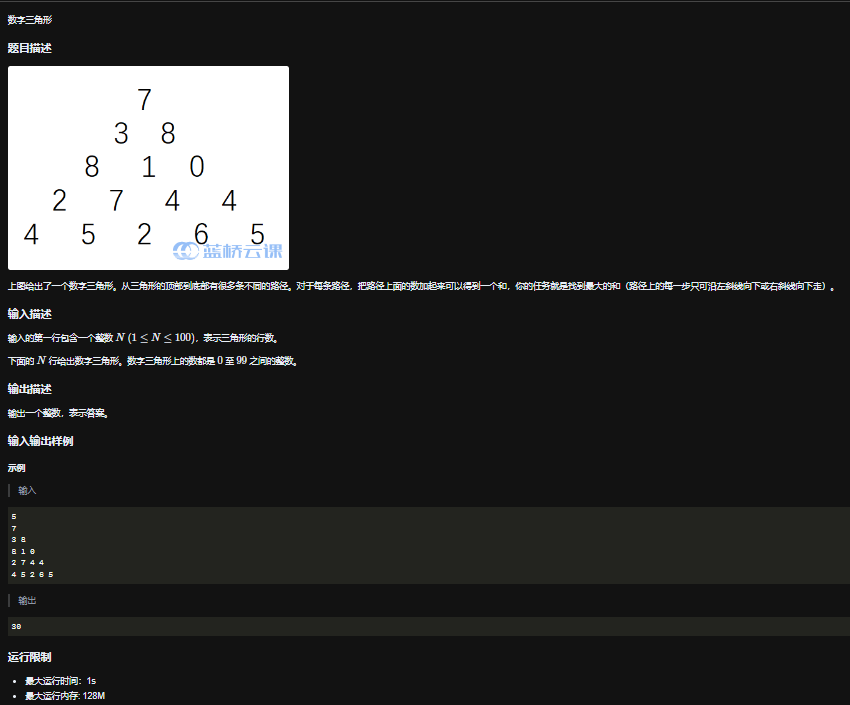
分析

状态：dp[i][j]表示第i行，第j列的和的最大值

状态迁移方程：方向从底向上，取当前位置的下一层的左边或右边的最大值与当前位置求和，作为当前位置dp值

最终状态：dp[1][1]

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.Scanner;

public class Main {
	static int MAXSIZE = 105;
	static int[][] dp = new int[MAXSIZE][MAXSIZE];
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		// 读入三角形里面的数据
		for(int i = 1; i <= n; i++) {
			for(int j = 1; j <= i; j++) {
				 dp[i][j] = scan.nextInt();
			}
		}
		// 
		for(int i = n - 1; i >= 1; i--) {
			for(int j = 1; j <= i; j++) {
				// 状态转移方程，不过是从下往上
				dp[i][j] += Math.max(dp[i + 1][j], dp[i + 1][j + 1]);
			}
		}
		System.out.println(dp[1][1]);
		scan.close();
	}
}

题目二

题干

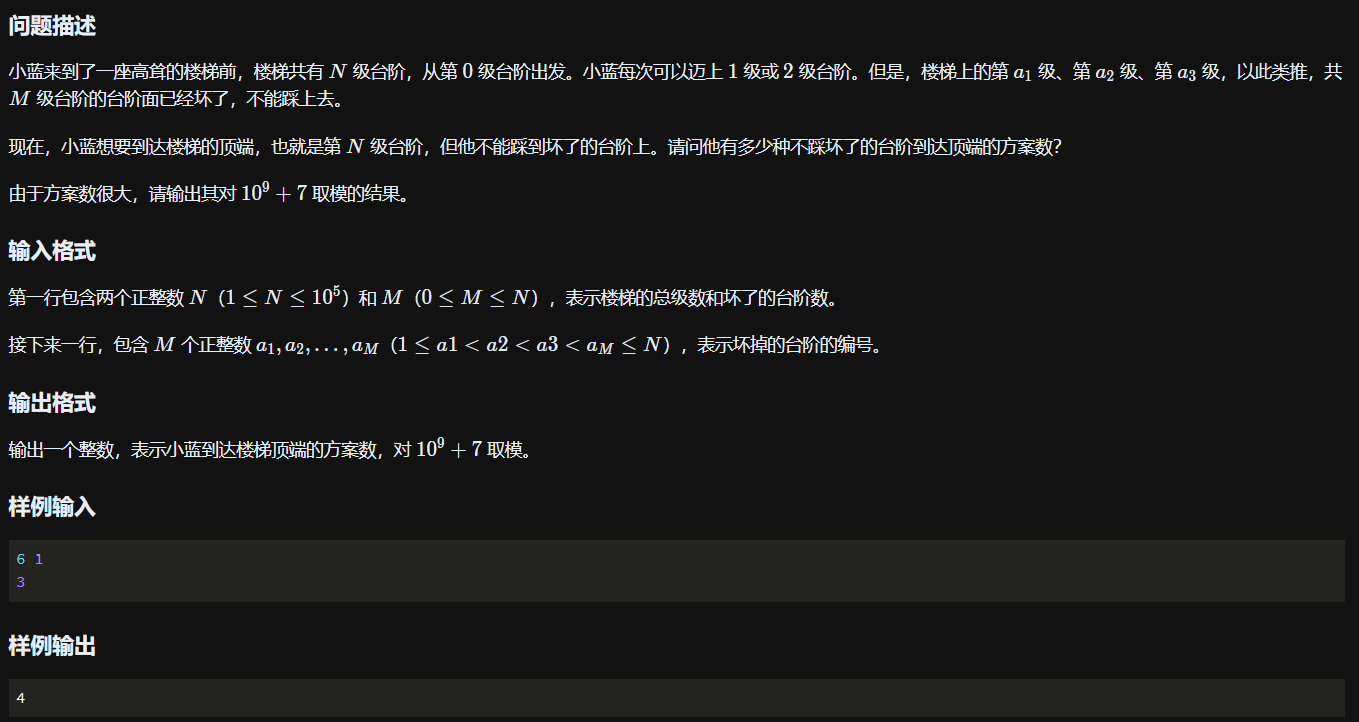
分析

确定状态：dp[i]表示到第i级台阶有多少种方案

确定状态转移方程：从后往前,dp[i] = dp[i - 1] + dp[i - 2]

确定最终状态：dp[N]

注意，题目中如果告诉你结果比较大，java一般需要开long

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.Scanner;

public class Main {
	static int p = (int)1e9 + 7;
	static int MAXSIZE = (int)10e5 + 5;
	static boolean[] broken = new boolean[MAXSIZE];
	static long[] dp = new long[MAXSIZE];
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int N = scan.nextInt();
		int M = scan.nextInt();
		for(int i = 0; i < M; i++) {
			int worse = scan.nextInt();
			broken[worse] = true;
		}
		// 第0级台阶
		broken[0] = false;
		dp[0] = 1;
		// 第一级台阶比较特殊，如果第一级台阶没有坏，则只用一种可能，就是从第0级台阶上来
		if(broken[1] == false) dp[1] = 1;
		for(int i = 2; i <= N; i++) {
			if(broken[i] == false) {
				dp[i] = (dp[i - 1] + dp[i - 2]) % p;
			} 
		}
//		for(int i = 1; i <= N; i++) {
//			System.out.print(dp[i] + " ");
//		}
//		System.out.println();
		System.out.println(dp[N]);
		scan.close();
	}
}

题目三

题干

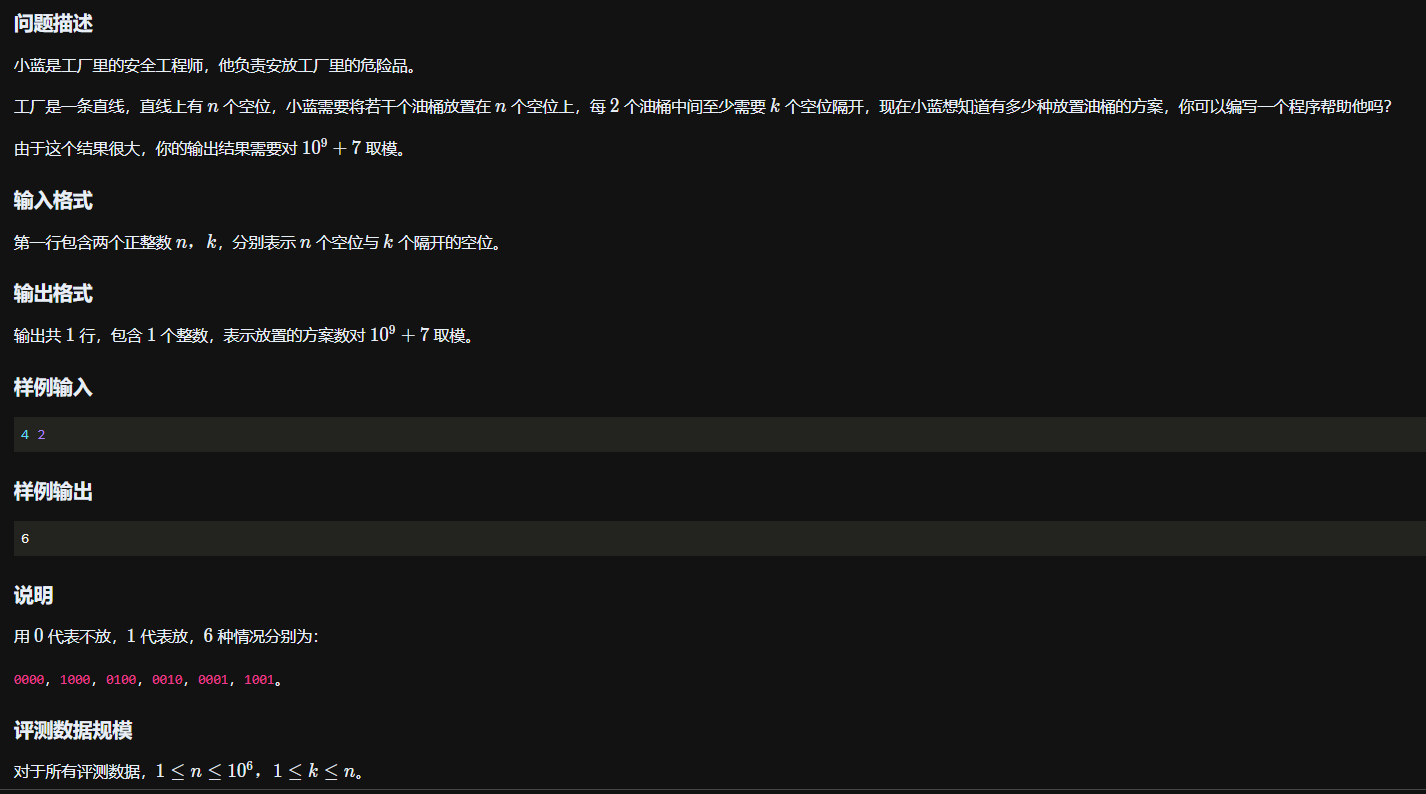
分析

确定状态

dp[i]:最后一个桶放在位置i的方案总数

状态转移方程

因为dp[i]表示最后一个桶在位置i所具有的方案总数，而要求最近的相邻两个桶之间要相隔k个桶，所以dp[i]等于从最后一个桶在位置1的方案(dp[1])到最后一个桶在位置i - k - 1的方案数(dp[i - k - 1])的和，即\(dp[j] = \sum_{i = 1}^{j - k - 1}dp[i]\)

最终状态

题目要求的是总方案数，由dp数列定义可知不是dp[N]，所以要对dp数组求前缀和，prefix[N]才是答案

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import java.util.Scanner;

public class Main {
	static int p = (int)1e9 + 7;
	static int N = (int)1e6 + 5;
	static long[] dp = new long[N];
	static long[] prefix = new long[N];
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int k = scan.nextInt();
		dp[0] = prefix[0] = 1;
		for(int i = 1; i <= n; i++) {
			if(i - k - 1 < 1) dp[i] = 1;
			else dp[i] =  prefix[i - k - 1];
			prefix[i] = (prefix[i - 1] + dp[i]) % p;
		}
		System.out.println(prefix[n]);
		scan.close();
	}
}

入门一题