命题与联结词
命题
判断结果惟一(非真即假)的陈述句
命题的真值 判断的结果
真值的取值 真与假
注意
感叹句、祈使句、疑问句都不是命题
陈述句中的悖论,判断结果不惟一确定的不是命题
举个例子
\(\sqrt{2}是有理数\) 是命题,但是是假命题
x + 5 > 3 不是命题
2050年元旦下大雪 是命题,但是真假未知
命题分类:简单命题(也称原子命题)与复合命题
简单命题符号化
用小写英文字母 \(p,q,r, …,p_i, q_i, r_i(i > 1)\)表示简单命题
用1表示真,用0表示假
举个例子
\(p:\sqrt{2}是有理数, 则p的真值为0\)
联结词
否定:\(\lnot\)
规定\(\lnot p\) 为真当且仅当p为假
合取: \(\land\)
p与q要同时为真才为真
析取:\(\lor\)
p与q之一为真即为真
相同或
举个例子
令p:2是素数,q:4是素数,\(p\lor q\)
排斥或
举个例子
p:王小红生于1975年,q:王小红生于1976年,
\((p\land \lnot q)\lor (\lnot p \lor q)\)
蕴含:\(\to\)
如果p,则q,记作\(p \to q\), p是前件,q是后件,规定\(p \to q\)为假当且仅当p为真q为假
注:
\(p \to q\)的逻辑关系:q为p的必要条件,这个很重要,直接区分了只要……就和只有……才的区别
当p为假时,\(p\to q\)恒为真,称为空证明
举例:

等价联结词:\(\leftrightarrow\)
命题公式及其赋值
命题变项与合式公式
命题变项
命题常项:简单命题
命题变项(命题变元):真值可以变化的陈述句
合式公式的递归定义
如果一个公式已经是合式公式,那么在基础上的运算产生的公式也是合式公式
合式公式的层次
(1)若公式A是单个命题变项,则称A为0层公式
- A是n+1层的前提,在于得到A的公式中最大层数是n
举个例子
\(A = B \land C\),其中B,C分别为i层和j层公式,则A的层数n =max(i,j)
举例
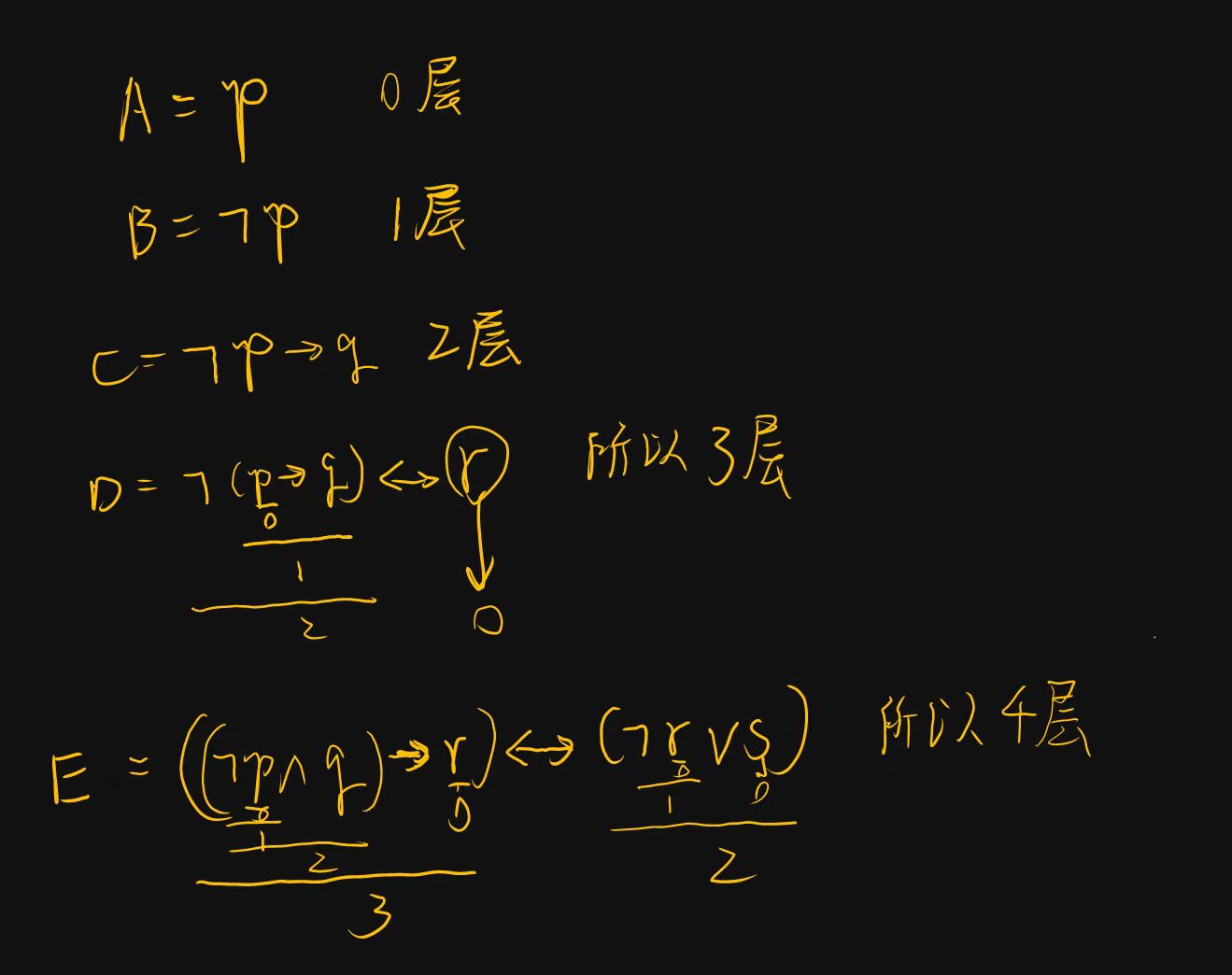
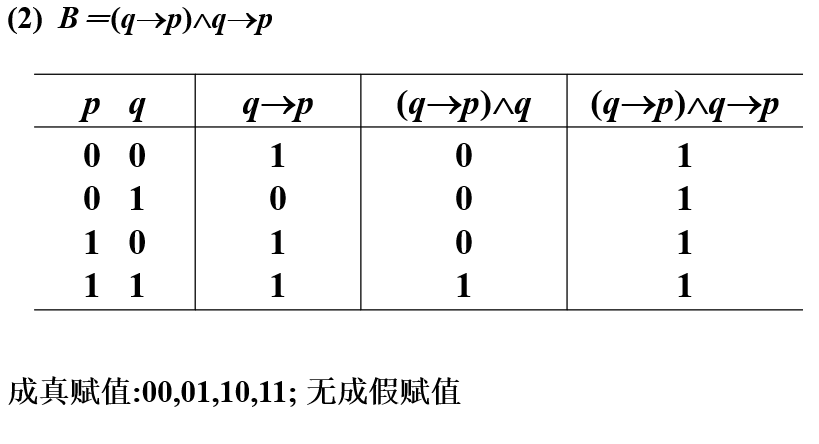
公式的赋值:使这个公式为真的赋值称作成真赋值,成假的就是成假赋值
注: 含n个命题变项的公式有\(2^n\)个赋值
真值表:从0列到\(2^n - 1\)
举个例子
公式的类型
重言式(永真式)
矛盾式(永假式)
可满足式
公式和真值表用途
n个命题变项,可以构成无穷多个合式公式,这些公式的真值表有\(2^{2^n}\)个不同的情况,因为有n个命题变项,每个有2种选择,有\(2^n\)种,结果又有2种选择,所以\(2^{2^n}\)