基本定义
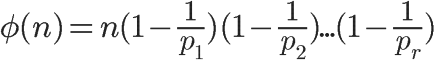
不过一般写程序不用上面的求法,而是用下面的思路与代码
找出n的因子,剔除含有n的因子的数
代码模板
1 | //求欧拉函数Φ(n) |
针对
1 | while(n % i == 0) { //从ans中删除i的倍数后,也要 |
和
1 | if (n > 1) { //若n大于1,则此时的n也是一个除1以外的因子 |
举例说明

举一反三
题目一
题目二
题目三
与上题几乎一样
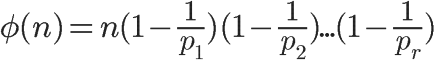
不过一般写程序不用上面的求法,而是用下面的思路与代码
找出n的因子,剔除含有n的因子的数
1 | //求欧拉函数Φ(n) |
针对
1 | while(n % i == 0) { //从ans中删除i的倍数后,也要 |
和
1 | if (n > 1) { //若n大于1,则此时的n也是一个除1以外的因子 |
举例说明

与上题几乎一样