Pilot's Blog
0%

softmax的定义与实现

发表于 更新于 分类于 ， Valine：
本文字数： 5.3k 阅读时长 ≈ 5 分钟
基于pytorch框架的对于softmax的定义和实现

基本术语的介绍

特征：（feature）：

描述一件事物的特性，如一个人的身高、体重、年龄和五官。

代码里就是用来表示某样事物的矩阵

样本（sample）：

由一个人的特征组成的数据，如{180,70,19,精致}{180,70,19,精致}。

代码里就是从整个数据集里抽取的一部分

标签（label）：

描述一件事物的特性，如一个人帅或丑、一个人的财富数量。注：特征和标记没有明确的划分，由于问题的不同可能导致

A问题的特征是B问题的标记，B问题的标记是A问题的特征。

在代码里面往往表示的是真正的结果

样例（example）：

由一个人的特征和标记组成的数据，如{180,70,19,精致,帅}{180,70,19,精致,帅}。

特征空间（feature space）：

特征向量（feature vector）：特征空间内的某一个具体的向量

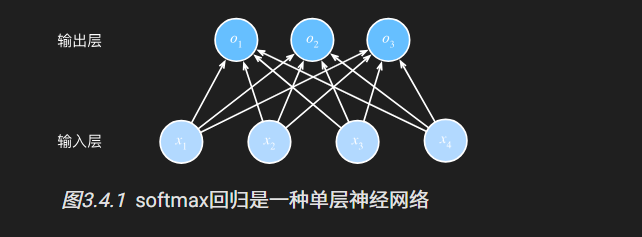
softmax回归

要解决的问题: 分类问题

从一个图像分类问题开始。 假设每次输入是一个2×2的灰度图像。 我们可以用一个标量表示每个像素值，每个图像对应四个特征\(x1,x2,x3,x4\)。 此外，假设每个图像属于类别“猫”“鸡”和“狗”中的一个。

独热编码： （1）一个向量，它的分量和类别一样多 （2）类别对应的分量设置为1，其他所有分量设置为0。 （3）举例：标签y将是一个三维向量， 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”：

优点：softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质

形成的网络架构

（1）估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出

（2）所以需要和输出一样多的仿射函数（affine function）(没那么高大上，就是实现映射关系的函数)， 每个输出对应于它自己的仿射函数

（3）有4个特征(因为前面说的灰度图有4个像素点）和3个可能的输出类别（猫，鸡，狗）

（4）所以需要12个标量来表示权重（带下标的\(w\)）， 3个标量来表示偏置（带下标的\(b\)），每个输入计算三个**（logit）：\(o1、o2和o3\)。

（5）所以softmax回归是一个单层神经网络。softmax回归的输出层也是全连接层

运算

1. 对每个项求幂（使用exp）；

2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；

3. 将每一行除以其规范化常数，确保结果的和为1。

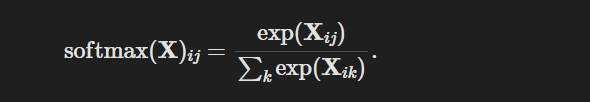
实现

读取数据集

练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模型

打乱数据集中的样本并以小批量方式获取数据

接收批量大小、特征矩阵和标签向量作为输入

生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。

读取第一个小批量数据样本并打印。 每个批量的特征维度显示批量大小和输入特征数。 同样的，批量的标签形状与batch_size相等。

1
2
3
4
5
6
7
8
9
def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])
        yield features[batch_indices], labels[batch_indices]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[[-0.594405    0.7975923 ]
 [ 0.5477517   0.15074243]
 [-0.34835348  0.929739  ]
 [-1.5249145   0.701587  ]
 [-2.298264    0.10911477]
 [ 1.6356094   0.14286116]
 [-0.19882555 -0.85171705]
 [ 1.2024101  -1.7029836 ]
 [-0.60534513 -0.39319903]
 [-1.771029   -0.5459446 ]]
 [[ 0.30207413]
 [ 4.786745  ]
 [ 0.33858034]
 [-1.2297847 ]
 [-0.75900215]
 [ 6.979927  ]
 [ 6.7001796 ]
 [12.39533   ]
 [ 4.3220677 ]
 [ 2.517848  ]]

定义模型

手搓版本

初始化模型参数

展平

每个样本都将用固定长度的向量表示。 原始数据集中的每个样本都是28×28 = 784的图像。 展平每个图像，把它们看作长度为784的向量

输出维度

输出与类别一样多。 因为我们的数据集有10个类别，所以网络输出维度为10

权重矩阵和偏置矩阵
大小

因此，权重将构成一个784×10（每个数据由一维列向量构成，这个一维向量由784个数字构成，一共有10个输出，每个输出对应的每一行就是一个公式)的权重矩阵， 偏置将构成一个1×10的行向量（每个输出对应一个偏置，一共10个输出），注意这里是“立”着来，从上往下计算，不像前面提到和一般从左到右

初始化

使用正态分布初始化我们的权重W，偏置初始化为0。

代码
1
2
3
4
5
6
num_inputs = 784
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
# 使用 PyTorch 的 torch.normal 函数生成行数为 num_inputs，列数为 num_outputs的二维矩阵，并且服从正态分布（均值为0，标准差为0.01），并设置 requires_grad=True
b = torch.zeros(num_outputs, requires_grad=True)

定义softmax操作

1. 对每个项求幂（使用exp）；
2. 对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
3. 将每一行除以其规范化常数，确保结果的和为1。

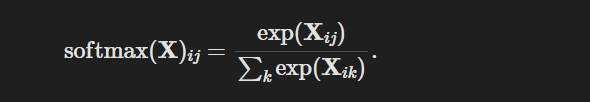##### 代码 

1
2
3
4
def softmax(X):
    X_exp = torch.exp(X)
    partition = X_exp.sum(1, keepdim=True)
    return X_exp / partition  # 这里应用了广播机制

其中sum操作，如果指定在一个轴（同一列（轴0）或同一行（轴1））上求和，

如果X是一个形状为(2, 3)的张量，我们对列进行求和

默认情况会降维，得到一个形状(3,)的向量

但keepdim=True指定保持在原始张量的轴数，将产生一个具有形状(1, 3)的二维张量

1
2
X = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]])
X.sum(0, keepdim=True), X.sum(1, keepdim=True)

输出结果

1
2
3
(tensor([[5., 7., 9.]]),
 tensor([[ 6.],
         [15.]]))

合并

1
2
def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

X.reshape((-1, W.shape[0]))：这一步将输入 X 重塑为一个二维张量，其形状的第二个维度与权重 W 的第一个维度相同。-1 表示该维度的大小会自动计算，以保持 X 中元素的总数不变

torch.matmul(X.reshape((-1, W.shape[0])), W)：这一步执行矩阵乘法，将重塑后的 X 与权重 W 相乘

。torch.matmul(X.reshape((-1, W.shape[0])), W) + b：这一步将偏置 b 加到矩阵乘法的结果上。注意，由于广播（broadcasting）机制，即使 b 的形状与矩阵乘法的结果不同，这一步也能正确执行。

softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)：最后，这一步将 softmax 函数应用到加上偏置的结果上。softmax 函数能将其输入（通常被称为 logits 或分数）转换为正值且和为 1 的概率分布。

导包版本

1
2
3
4
5
6
7
8
# PyTorch不会隐式地调整输入的形状,我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);
1
2
# 直接将模型定义和损失函数合并到一起去了
loss = nn.CrossEntropyLoss(reduction='none')

定义损失函数

损失函数是什么

量化目标的实际值与预测值之间的差距

选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0

回归问题中最常用的损失函数是平方误差函数 ### 对数似然(就是大二上学的概率论里的第六章的最大似然估计，与矩估计并列)

交叉熵损失

观察到的不仅仅是一个结果，现在用一个概率向量表示，如(0.1,0.2,0.7)， 而不是仅包含二元项的向量(0,0,1)。使用下面这个公式定义损失，它是所有标签分布的预期损失值。称为交叉熵损失（cross-entropy loss）

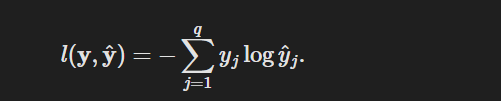实现交叉熵损失函数

1
2
3
4
def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])

cross_entropy(y_hat, y)

定义优化算法

每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。 接下来，朝着减少损失的方向更新我们的参数

接受模型参数集合、学习速率和批量大小作为输入。

每 一步更新的大小由学习速率lr决定

计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

1
2
3
4
5
6
def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

分类精度：确预测数量与总预测数量之比

须输出硬预测（hard prediction）时， 我们通常选择预测概率最高的类

当预测与标签分类y一致时，即是正确的。

计算方法：

如果y_hat是矩阵，那么假定第二个维度存储每个类的预测分数。 我们使用argmax获得每行中最大元素的索引来获得预测类别。 然后我们将预测类别与真实y元素进行比较。 由于等式运算符“==”对数据类型很敏感， 因此我们将y_hat的数据类型转换为与y的数据类型一致。 结果是一个包含0（错）和1（对）的张量。 最后，我们求和会得到正确预测的数量。

举例说明

1
2
3
4
5
6
y = torch.tensor([0, 2])
# 标签y, 在第一个样本中，第一类是正确的预测； 而在第二个样本中，第三类是正确的预测
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
# y_hat包含2个样本在3个类别的预测概率， 以及它们对应的标签y
y_hat[[0, 1], y]
# 对一个二维张量 y_hat 进行索引。具体来说，它选择了 y_hat 的第 0 行和第 1 行中，由 y 指定的列

输出 

1
tensor([0.1000, 0.5000])
定义计算精度的函数 
1
2
3
4
5
6
def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)
    cmp = y_hat.type(y.dtype) == y
    return float(cmp.type(y.dtype).sum())

使用之前定义的变量y_hat和y分别作为预测的概率分布和标签，第一个样本的预测类别是2（该行的最大元素为0.6，索引为2），这与实际标签0不一致。 第二个样本的预测类别是2（该行的最大元素为0.5，索引为2），这与实际标签2一致。 因此，这两个样本的分类精度率为0.5。

1
accuracy(y_hat, y) / len(y)

输出

1
0.5

训练

在每次迭代中，我们读取一小批量训练样本

通过调用模型来获得一组预测并计算损失l（前向传播）

计算完损失后，开始反向传播来计算每个参数的梯度。

最后，我们调用优化器(比如sgd)来更新模型参数。

预测