Pilot's Blog
0%

洛谷2008SODI仪仗队

发表于 更新于 分类于 ， ， Valine：
本文字数： 1.2k 阅读时长 ≈ 1 分钟
利用欧拉函数

题目

题目描述

作为体育委员，C 君负责这次运动会仪仗队的训练。仪仗队是由学生组成的 \(N \times N\) 的方阵，为了保证队伍在行进中整齐划一，C 君会跟在仪仗队的左后方，根据其视线所及的学生人数来判断队伍是否整齐（如下图）。

现在，C 君希望你告诉他队伍整齐时能看到的学生人数。

输入格式

一行，一个正整数 \(N\)。

输出格式

输出一行一个数，即 C 君应看到的学生人数。

样例输入

1
4

样例输出

1
9

提示

对于 \(100 \%\) 的数据，\(1 \le N \le 40000\)。

分析

要求的就是从原点看，能看到几个点（原点不考虑，就是如果n = 1，那么就只有1个人，就是观察者本身，那么他看不到其他人）

举个例子，如果n=4

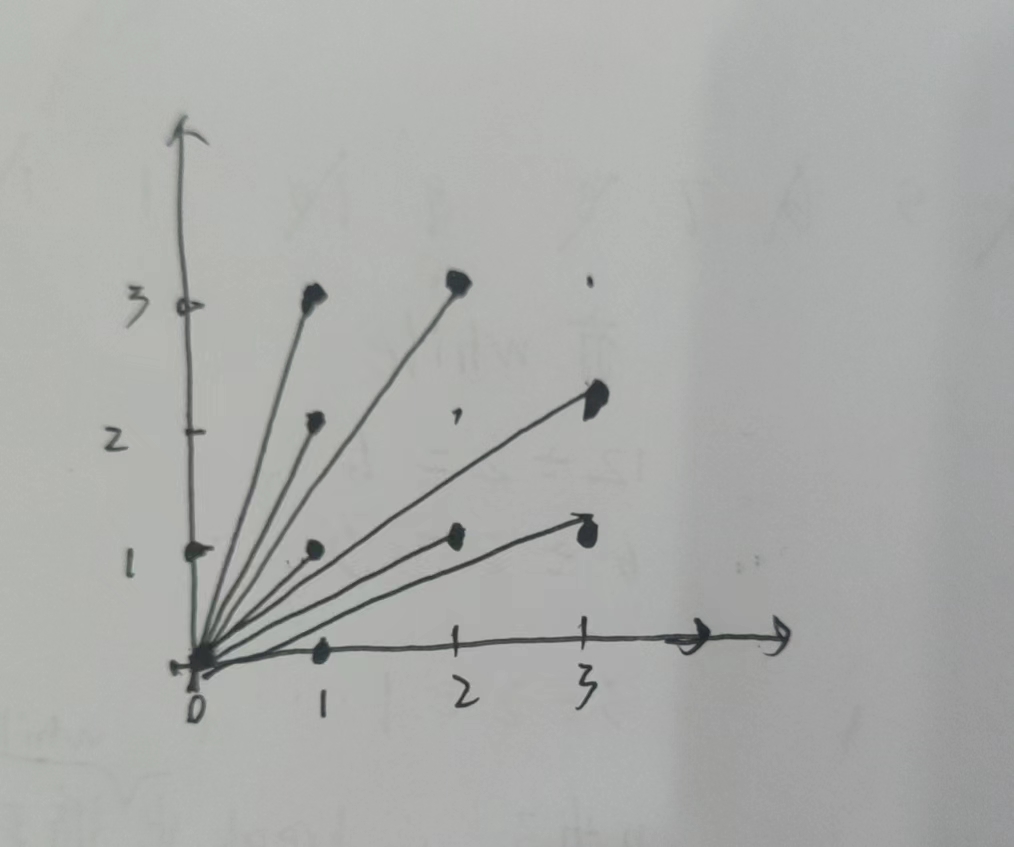
可以看出是9个

那么怎么推出一般情况呢

首先发现点关于y = x 对称，所以只用研究一半就行，又因为（1，1）这个点比较特殊，所以将(0, 1)(1, 0)(1, 1)这三个点另外看，从i = 2开始分析

发现从i = 2到 i = n - 1, 要能看到，说明没有遮挡，即x与y互质，所以就是求\(\sum_{i = 2}^{n - 1}\sum_{j = 0}^{j = i}[gcd(i, j) = 1]\)（求和公式从左往右看），而\(\sum_{j = 0}^{j = i}[gcd(i, j) = 1]\)就是\(\varphi(i)\)，所以最终计算结果就是$ 3 + 2 *_{i = 2}^{n - 1}(i)$

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		int ansSum = 0;
		for(int i = 2; i < n; i++) {
			ansSum += 2 * eulr(i);
		}
		if(n == 1) {
			System.out.println(0);
		} else {
			ansSum += 3;
			System.out.println(ansSum);
			scan.close();			
		}
	}
	static int eulr(int n) {
		int ans = n;
		for(int i = 2; i * i <= n ; i++) {
			if(n % i == 0) {
				ans -= ans / i;
				while(n % i == 0) {
					n /= i;
				}
			}
		}
		if(n > 1) {
			ans -= ans / n;
		}
		return ans;
	}
}

类似(或者说一模一样的题目)

区别在于两题对于n的定义，上一题n包含观察者本身，这一题则不包含；比如n=1的时候，上一题结果为0，本题则是3