Pilot's Blog
0%

第三章-命题逻辑的推理理论

发表于 更新于 分类于 ， Valine：
本文字数： 2.4k 阅读时长 ≈ 2 分钟

推理的形式结构

推理的正确与错误

设 A1, A2, ..., Ak, B 为命题公式。若对于每一组赋值，当 A1 ∧ A2 ∧ ... ∧ Ak 为假时，或者当 A1 ∧ A2 ∧ ... ∧ Ak 为真时，B 也为真，则称由前提 A1, A2, ..., Ak 推出结论 B 的推理是有效的或正确的，并称 B 是有效结论。

推理的形式结构

  1. {A1, A2, …, Ak} ⊢ B 若推理正确，记为 {A1, A2, ..., An} ⊢ B 记Γ = {A1, A2, …, Ak}，则 Γ ⊢ B. 若推理正确，则 Γ ⊢ B.
  2. \((A1 ∧ A2 ∧ … ∧ Ak \rightarrow B) 若推理正确，记为 (A1 ∧ A2 ∧ … ∧ Ak \Rightarrow B)\)
  3. 前提：(A1, A2, ..., Ak) 结论：(B)

判断推理正确的方法

  1. 真值表法
  2. 等值演算法
  3. 主析取范式法

举例：

判断下面推理是否正确 (1) 若今天是1号, 则明天是5号. 今天是1号. 所以, 明天是5号.
(2) 若今天是1号, 则明天是5号. 明天是5号. 所以, 今天是1号.

首先表示（1）

用等值演算法

用主析取范式，以（2）为例

推理定律(重点)

推理定律的条件（箭头前的部分都是1）

  1. \(A \Rightarrow (A \lor B)\) 附加律 (如果命题A为真，那么命题A或B为真)
  2. \((A \land B) \Rightarrow A\) 化简律
  3. \((A \Rightarrow B) \land A \Rightarrow B\) 假言推理
  4. \((A \Rightarrow B) \land \lnot B \Rightarrow \lnot A\) 拒取式
  5. \((A \lor B) \land \lnot B \Rightarrow A\) 析取三段论
  6. \((A \Rightarrow B) \land (B \Rightarrow C) \Rightarrow (A \Rightarrow C)\) 假言三段论
  7. \((A \Leftrightarrow B) \land (B \Leftrightarrow C) \Rightarrow (A \Leftrightarrow C)\) 等价三段论
  8. \((A \Rightarrow B) \land (C \Rightarrow D) \land (A \lor C) \Rightarrow (B \lor D)\) 构造性二难 \((A \Rightarrow B) \land (\lnot A \Rightarrow B) \Rightarrow B\) 构造性二难(特殊形式)
  9. \((A \Rightarrow B) \land (C \Rightarrow D) \land (\lnot B \lor \lnot D) \Rightarrow (\lnot A \lor \lnot C)\) 破坏性二难

每个等值式可产生两个推理定律 如，由 \(A \Leftrightarrow \lnot \lnot A\) 可产生 \(A \Rightarrow \lnot \lnot A\) 和 \(\lnot \lnot A \Rightarrow A\)

自然推理系统P

形式系统的定义与分类

自然推理系统P

字母表

  1. 命题变项符号：p, q, r, …, pi, qi, ri, …
  2. 联结词符号：¬, ∧, ∨, →, ↔︎
  3. 括号与逗号：(, ), ，

合式公式（同定义1.6）

有限次地应用联结词和括号形成的命题符号串是合式公式

推理规则(重点中的重点)

  1. 前提引入规则
  2. 结论引入规则
  3. 置换规则（就是德摩根律）

注：

假言推理在于蕴含式前提为真

拒取式规则在于蕴含式结论为假

假言三段论在于递推

析取三段论或的一方为假

在P中构造证明:直接证明法、附加前提证明法、归谬法

直接证明法

举例：

构造下面推理的证明：

​ 若明天是星期一或星期三, 我明天就有课. 若我明天有课, 今天必备课. 我今天没备课. 所以, 明天不是星期一,

也不是星期三.

附加前提证明法

欲证

前提：(A1, A2, …, Ak)

结论：\(C \Rightarrow B\)

等价地证明

前提：(A1, A2, …, Ak, C)

结论：B

理由： \((A1 \land A2 \land … \land Ak) \Rightarrow (C \Rightarrow B)\)

\(\equiv \lnot (A1 \land A2 \land … \land Ak) \lor (\lnot C \lor B)\)

\(\equiv \lnot (A1 \land A2 \land … \land Ak \land C) \lor B\)

\(\equiv (A1 \land A2 \land … \land Ak \land C) \Rightarrow B\)

适用于结论为蕴涵式，本质就是将本来结论中的前提也作为条件

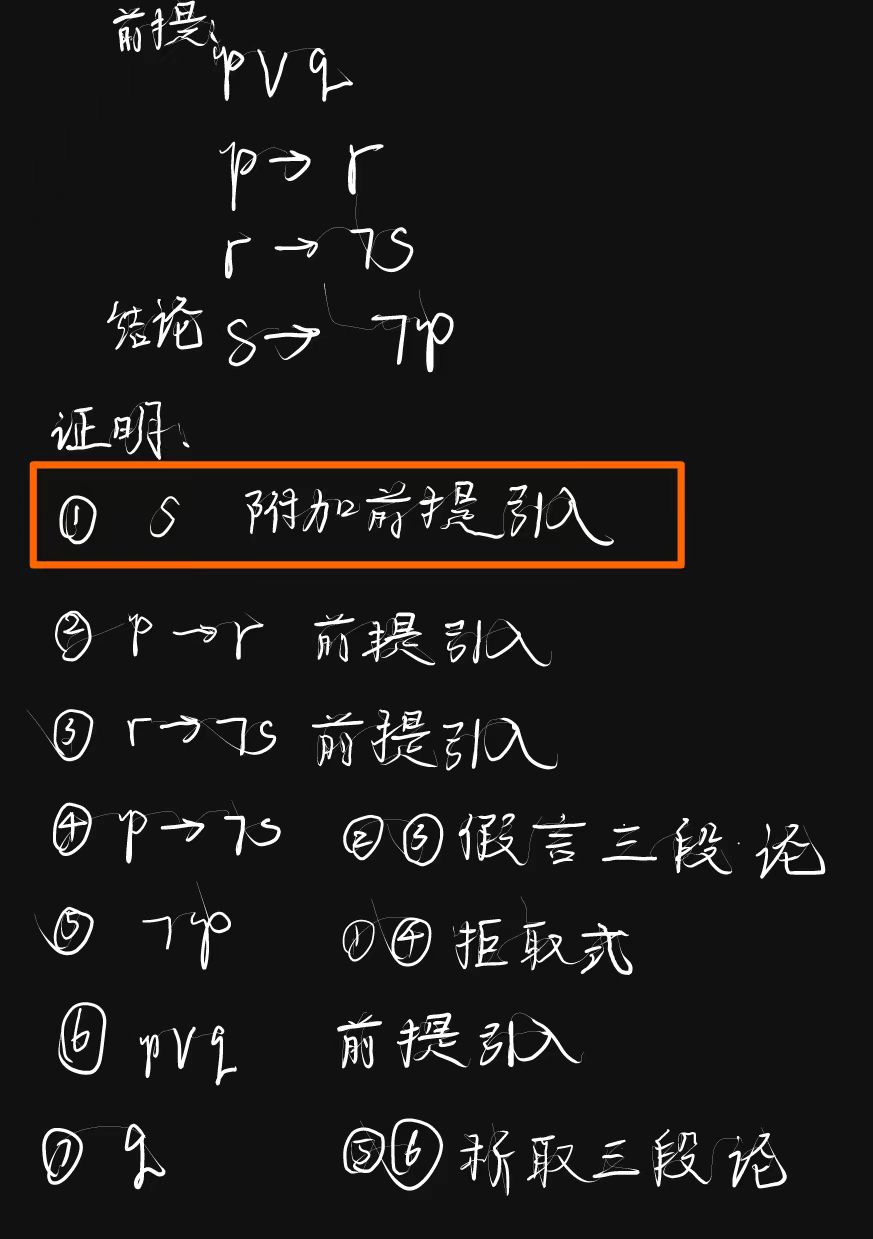
举例:构造下面推理的证明:

"2是素数或合数. 若2是素数, 则 () 是无理数. 若 () 是无理数, 则4不是素数. 所以, 如果4是素数, 则2是合数."

归谬法（反证法）

欲证

前提：(A1, A2, … , Ak)

结论：(B)

做法

在前提中加入\(\lnot B\)，推出矛盾

理由：

\(A1\land A2\land …\land Ak\Rightarrow B\)

\(\equiv \lnot(A1\land A2\land …\land Ak)\lor B\)

\(\equiv \lnot(A1\land A2\land …\land Ak\land\lnot B)\)

\(\equiv \lnot(A1\land A2\land …\land Ak\land\lnot B)\lor 0\)

\(\equiv A1\land A2\land …\land Ak\land\lnot B\Rightarrow 0\)

举例：

前提：\(\lnot(p\land q))\lor r\), \(r\Rightarrow s\), \(\lnot s\), \(p\)
结论：\(\lnot q\)

消解证明法

基本做法：

  1. 把前提中的公式,结论的否定都化成等值的合取范式

  2. 列出所有合取范式的所有简单析取式作为前提

  3. 用消解规则构造证明.

  4. 如果得到空式(就是矛盾），则证明推理是正确的.

举例

前提：\(q\Rightarrow p\), \(q\Leftrightarrow s\), \(s\Leftrightarrow t\), \(t\land r\)

结论：\(p\land q\land s\)