排序

插入排序

直接插入排序：不断从无序序列中挑选出元素插入有序序列

折半插入排序：先折半查找出待插入位置，再统一移动

希尔排序：每次取不同的步长，按步长从原序列里挑出子序列，直到最后步长为0

举例1：

交换排序

冒泡排序：

每轮排序结果确定1个位置，可以从最后一个开始，也可以从第一个开始

每轮排序过程中比较交换两个相邻的元素

快排：主要思想是分治，pivot前都比它小，pivot后都比它大，再对左右子序列继续选pivot，分解

一轮分治过程中，high和low依次运行

首先high运行，当high所指元素小于pivot时，high所指元素放到low指的地方（认为每次停下来i的那个（high/low）指向的位置为空)

然后low开始运行，当low所指元素大于pivot时，low所指元素放到high所指位置

不断循环直到low == high,将pivot放到i与j此时指向的位置

快排每次分治都有1个元素被放到最终位置

/*Partition函数参数是待划分序列，开头位置（low指针指向的位置）结尾位置（high指针指向的位置），返回最终pivot的位置*/
int Partition(int data[], int high, int low) {
    int pivot = data[low];
    while(low < high) {
        while(low < high && data[high] >= pivot) high--;
        data[low] = data[high];
        while(low < high && data[low] <= pivot) low++;
        data[high] = data[low];    
    }   
    data[low] = pivot;
    return low;
}
/*QuickSort函数参数是待划分序列，开头位置（low指向位置），结尾位置（high指向位置）*/
void QuickSort(int data[], int low, int high) {
    if(low < high) {
        int pivotPosition = Partition(data, low, high);
        QuickSort(data, low, pivotPosition - 1);    //对左子表再快排
        QuickSort(data, pivotPosition + 1, high);   //对右子表再快排
    }
}

举例1：判断排序结果

1 写出最终排序结果 2 逐个选项选出已经放到应该排的位置的元素，因为针对每一个子列排序，都会有一个元素排到它应该排的位置，所以排第n趟的时候至少有n个元素已经放到正确位置 3 再看每个放到正确位置元素将原序列分成几段，因为如果每趟的pivot恰好放在端的地方，那么就是排第n趟的时候有n个元素归位，但如果分割了原序列，就是n+1

选择排序

简单选择排序：每次确定一个元素位置，比如确定最后一个，就是最大元素，比较范围从1~n-1，确定倒数第二个，比较范围从1到n-1……以此类推

堆排序

1 存储与结构

1.1 树形结构

堆的最常用结构是二叉树，且一般是完全二叉树

1.2 存储结构

堆实际存储一般不用指针，而是使用数组，如下图

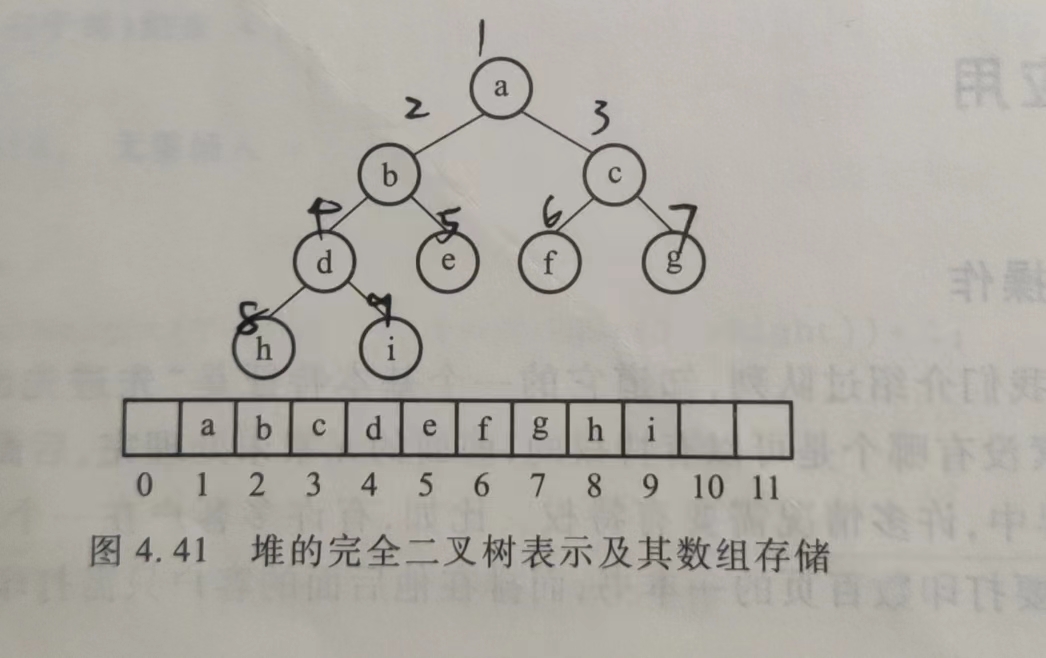
1.3 数组下标关系

1. 起始存储单元为1，而不是0, 0作为哨兵，且也易于从子节点找到父节点

2. 对于下标为i的节点，父节点下标是i/2向下取整，反过来，对于下标为i的节点，左孩子下标是2 * i，右孩子是 2 * i + 1

2 操作

2.1 插入

以大顶堆为例

先将待插入节点放到数组最后一位

然后向上上滤寻找插入位置，即与父节点比较，如果比父节点大，那么就把父节点下放，直到找到待插入节点应该插入的位置

但是注意到，如果插入的新节点比原堆中任意元素都大，那么到堆顶（下标为1）的时候又/=2得0，0不断/=2得0陷入死循环，所以如果已知堆中元素范围，可以将下标0设置为大于堆中可能元素，这样循环到0就一定会退出

代码如下

#define MAX_NUM 1000000
void Insert(int data[], int x, int size) {
    int i = ++size;	//因为要插入元素，所以大顶堆size + 1
    for(; data[i / 2] < x; i /= 2) {	//向上寻找插入位置
        data[i] = data[i / 2];			//将父节点下放
    }	
    data[i] = x;	//将新节点插入到应该插入的位置
}

2.2 删除

以大顶堆为例

先弹出根节点

然后取数组中最后一个元素（因为它在大顶堆中必然是叶子节点）向下下滤寻找插入位置

通过与当前层为根节点（此时为空）的左右子树中最大值比较，如果左右子树中最大值比最后一个元素大，就将左右子树中最大值上移，接着从上移节点的位置（此时为空）继续向下比较，否则将最后一个元素插入当前层为根节点

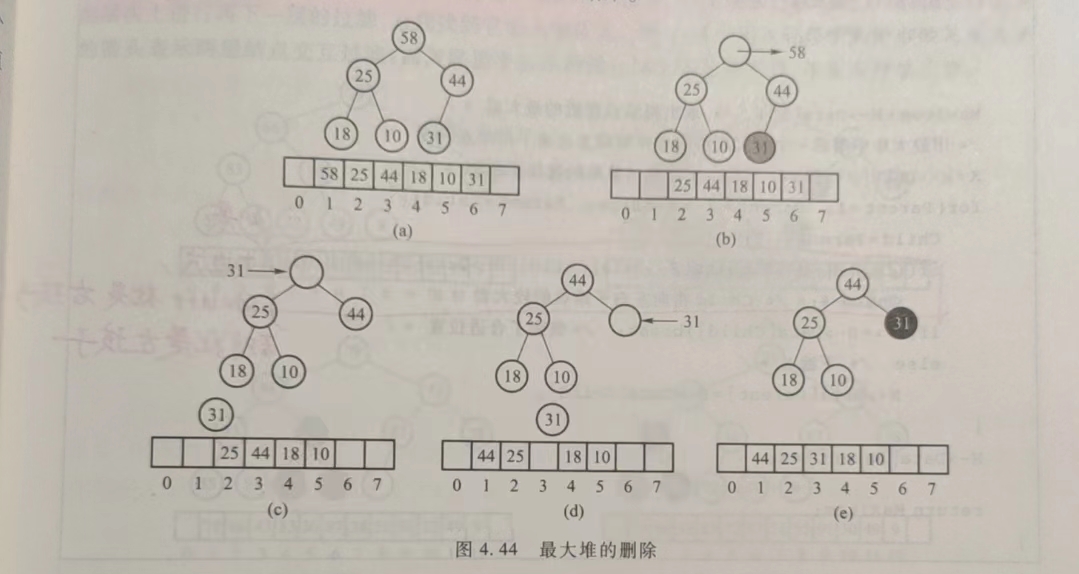
代码

int PopMax(MaxHeap maxHeap) {
	int maxData = maxHeap->Data[1];
    int x = maxHeap->Data[maxHeap->Size--];	//选择原来大顶堆中最后一个存储的元素来下滤
    int parent = 1;
    int child;
    for(; parent * 2 <= maxHeap->Size; parent = child) {
        child = parent * 2;
        if(child != maxHeap->Size && maxHeap->Data[child] < maxHeap->Data[child + 1]) {
			child = child + 1;
        }
        if(x < maxHeap->Data[child]) {	//将x与child比较，注意这时parent指向的位置为空, 如果小就将child提上来
            maxHeap->Data[parent] = maxHeap->Data[child];
        } else {	//如果x比child大就break出循环，注意不能在循环里赋值，具体还不清楚，但在循环里就把x赋给parent会报错
            break;
        }
    }
    maxHeap->Data[parent] = x;
    return maxData;
}

归并排序

一算法思想：分治

不过归并分治过程和快排有区别

快排是先对一个大序列(在一个大序列中找到pivot，利用pivot将大序列分割成左右两个小序列)操作，再分割成小序列

归并是先分割成小序列(先将大序列分割成小序列) ，再操作(对将小序列两个两个归并成一个大序列)

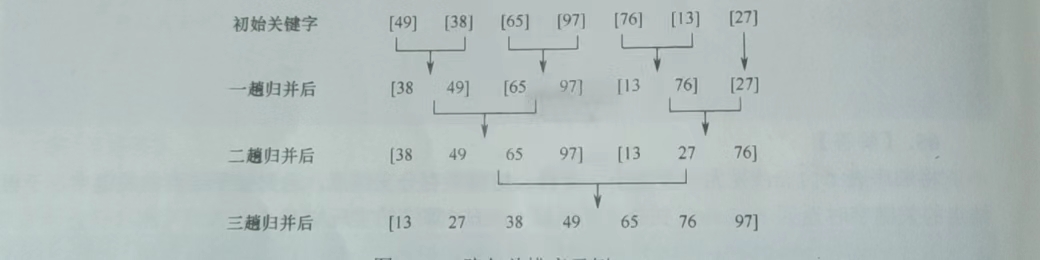
1 “分”：分割成小序列

2 治：小序列两个两个合并成大序列

2.1 开一个辅助数组B

2.2 将待排数组(名义上两个，但实际上存在一个里面)存放到辅助数组里面

2.3 这时待排数组为空，利用两个指针(分别指示待归并的两个数组的起点)在辅助数组上移动，将其中大的重新拷贝回待排数组

2.4 如果其中一个指针移动的位置超过了原来对应待归并的数组的范围，将剩下一个数组里元素全部拷贝回待排数组

二代码

Merge()(用来合并两个序列)

int Assistance[MAXNUM];
void Merge(int data[], int low, int high, int mid) {
    /*拷贝到辅助数组*/
    for(int i = 0; i < high; i++) {
        Assistance[i] = data[i];
    }
    int p, q, r;
    for(p = low, q = mid + 1, r = low; p <= mid && q <= high; ) {
        if(Assistance[p] > Assistance[q]) {
            data[r++] = Assistance[q];
        } else {
            data[r++] = Assistance[p];
        }
    }
    while(p <= mid) data[r++] = Assistance[p];
    while(q <= high) data[r++] = Assistance[q]; 
}

MergeSort()(用来分割)

void MergeSort(int data[], int low, int high) {
    if(low < high) {
        int mid = (low + high) / 2;
        MergeSort(data, low, mid);
        MergeSort(data, mid + 1, low);
        Merge(data, low, high, mid);
    }
}

排序