一阶逻辑等值式与置换规则

基本等值式

第一组:命题逻辑中16组基本等值式

就是下面这些东西

第二组

消去量词等值式

说白了就是任意就是将所有情况并起来，存在就是将所有情况和起来

设D = {a1, a2, … , an}

① ∀xA(x) ⇔ A(a1)∧A(a2)∧…∧A(an)

② ∃xA(x) ⇔ A(a1)∨A(a2)∨…∨A(an)

量词否定等值式

① ¬∀xA(x) ⇔ ∃x¬A(x)(任意的非就意味着存在非的情况)

② ¬∃xA(x) ⇔ ∀x¬A(x)(存在的非就意味着任意都是非)

量词辖域收缩与扩张等值式。

1. 收缩是指收到约束变量，把自由变量扔出去，扩张就是将自由变量也考虑进来

2. 无论是∨还是∧收缩辖域时，∀或者∃都只能对含约束变量的作用

3. →收缩辖域时，∀或者∃如果约束变量在前面需要取反,如果约束变量在后面就不用取反

关于全称量词的：

①∀x(A(x)∨B) ⇔ ∀xA(x)∨B

②∀x(A(x)∧B) ⇔ ∀xA(x)∧B

③∀x(A(x)→B) ⇔ ∃xA(x)→B

④∀x(B→A(x)) ⇔ B→∀xA(x)

关于存在量词的：

①∃x(A(x)∨B) ⇔ ∃xA(x)∨B

②∃x(A(x)∧B) ⇔ ∃xA(x)∧B

③∃x(A(x)→B) ⇔ ∀xA(x)→B

④∃x(B→A(x)) ⇔ B→∃xA(x)

量词分配等值式

1. 与前面收缩扩张的区别在于，将∀（或者∃）分配给所有约束变量

2. ∀对∨，∃对∧无分配律

① ∀x(A(x)∧B(x)) ⇔ ∀xA(x)∧∀xB(x)

② ∃x(A(x)∨B(x)) ⇔ ∃xA(x)∨∃xB(x)

置换规则、换名规则、代替规则

置换规则

等价交换

设ϕ(A)是含A的公式，那么，若A⇔B，则ϕ(A)⇔ϕ(B).

换名规则

指导变元和约束变量要换一起换

设A为一公式，将A中某量词辖域中一个个体变项的所有约束出现及相应的指导变元换成该量词辖域中未曾出现过的某个个体变项符号，其余部分不变，设所得公式为A'，则A'⇔A.

代替规则

自由出现自个玩

设A为一公式，将A中某个个体变项的所有自由出现用A中未曾出现过的个体变项符号代替，其余部分不变，设所得公式为A'，则A'⇔A.

举例：

例1 将下面命题用两种形式符号化, 并证明两者等值: (1) 没有不犯错误的人

视频讲解

不是所有的人都爱看电影

例2：将公式化成等值的不含既有约束出现、又有自由出现的个体变项：

∀x(F(x,y,z)→∃yG(x,y,z))

例3：设个体域D={a,b,c}，消去下述公式中的量词:

∀x∃y(F(x)→G(y))

一阶逻辑前束范式

1. 指导变元必须在一起

2. 指导变元前不能有非

3. 这一条不是必须，但往往遵守，就是不同辖域的指导变元尽量不要重名

例如， ∀x¬(F(x)∧G(x)) ∀x∃y(F(x)→(G(y)∧H(x,y))) 是前束范式而 ¬∃x(F(x)∧G(x)) ∀x(F(x)→∃y(G(y)∧H(x,y))) 不是前束范式,

举例：

求下列公式的前束范式:

∀xF(x)∧¬∃xG(x)

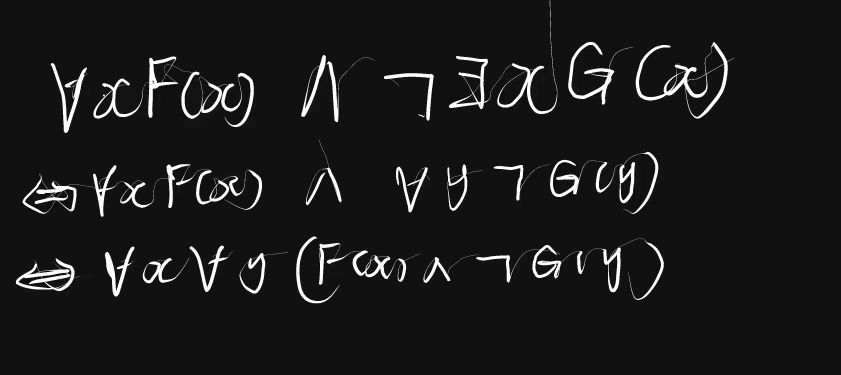
上面这个例子就是呼应了第三点不同指导变元尽量不要重名

∀x(F(x)→∃y(G(x,y)∧¬H(y)))

一阶逻辑的推论理论

推理定律

重言蕴涵式

1. A ⇒ (A∨B)                                                   附加律 
2. (A∧B) ⇒ A                                                   化简律
3. (A→B)∧A ⇒ B                                                 假言推理
4. (A→B)∧¬B ⇒ ¬A                                               拒取式    
5. (A∨B)∧¬B ⇒ A                                                析取三段论
6. (A→B)∧(B→C) ⇒ (A→C)                                         假言三段论
7. (A↔B)∧(B↔C) ⇒ (A↔C)                                         等价三段论
8. (A→B)∧(C→D)∧(A∨C) ⇒ (B∨D)                                   构造性二难
    (A→B)∧(¬A→B) ⇒ B                                           构造性二难(特殊形式)
9. (A→B)∧(C→D)∧(¬B∨¬D) ⇒ (¬A∨¬C)                               破坏性二难

基于基本等值式

1. 零律: A∨1 ⇔ 1, A∧0 ⇔ 0
2. 同一律: A∨0 ⇔ A, A∧1 ⇔ A
3. 排中律: A∨¬A ⇔ 1
4. 矛盾律: A∧¬A ⇔ 0
5. 蕴涵等值式: A→B ⇔ ¬A∨B
6. 等价等值式: A↔B ⇔ (A→B)∧(B→A)
7. 假言易位: A→B ⇔ ¬B→¬A
8. 等价否定等值式: A↔B ⇔ ¬A↔¬B
9. 归谬论: (A→B)∧(A→¬B) ⇔ ¬A

量词分配蕴涵律

(1) ∀x(A(x)∨∀xB(x)) ⇒ ∀x(A(x)∨B(x)) 

(2) ∃x(A(x)∧B(x)) ⇒ ∃xA(x)∧∃xB(x)

(3) ∀x(A(x)→B(x)) ⇒ ∀xA(x)→∀xB(x)

(4) ∃x(A(x)→B(x)) ⇒ ∃xA(x)→∃xB(x)

量词消去引入规则

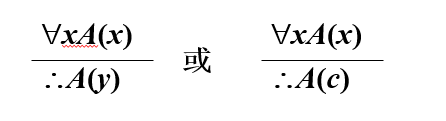
全称量词消去规则(∀-)

其中 x, y 是个体变项符号，c 是个体常项符号，并且在 A 中 x 不在 ∀y 和 ∃y 的辖域内自由出现

来解释下这句绕口令一样的话

举例：

要特别注意使用∀-, ∀+, ∃-, ∃+规则的条件。就是上面那句像绕口令的话

反例1. 对 A = ∀x∃yF(x,y) 使用 ∀-规则，推得 B = ∃yF(y,y)。取解释 I：个体域为 R，F(x, y): x > y 在 I 下 A 被解释为 ∀x∃y(x>y)，真；而 B 被解释为 ∃y(y>y)，假。原因：在 A 中 x 自由出现在 ∃y 的辖域 F(x,y) 内。

将上述段落重新打印。

全称量词引入规则（∀+）

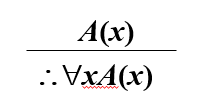
其中 x 是个体变项符号，并且不在前提的任何公式中自由出现

举例：

反例2. 前提: P(x)→Q(x), P(x) 结论: ∀xQ(x) 取解释I: 个体域为Z, P(x):x是偶数， Q(x):x被2整除

在 I 下前提为真，结论为假，从而推理不正确

错误的证明如下

“证明”: ① P(x)→Q(x) 前提引入 ② P(x) 前提引入 ③ Q(x) ①②假言推理 ④ ∀xQ(x) ③∀+

错误原因: 在④使用∀+规则，而 x 在前提的公式中自由出现。

存在量词消去规则（∃-）

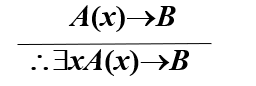
其中x是个体变项符号, 且不在前提的任何公式和B中自由出现

存在量词引入消去规则（∃+）

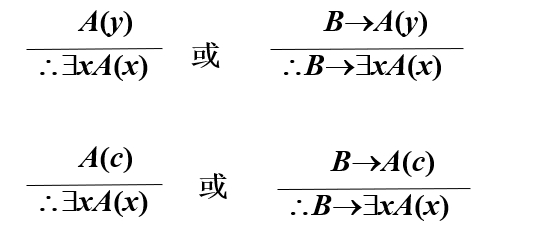
其中 x, y 是个体变项符号，c 是个体常项符号，且在 A 中 y 和 c 不在 ∀x 和 ∃x 的辖域内自由出现。

自然推理系统的证明

举例：

Pilot's Blog

第五章-一阶逻辑等值演算与推理