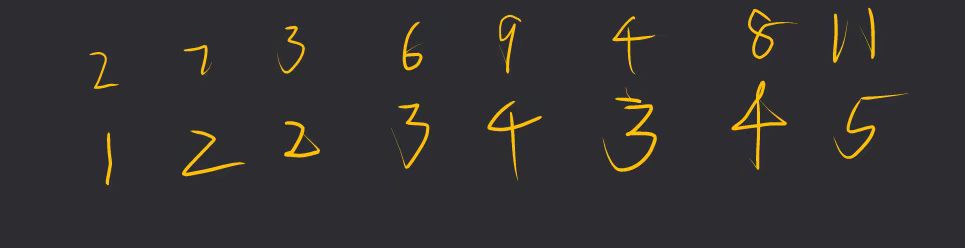Pilot's Blog
0%

算法设计与分析理论习题

发表于 更新于 分类于 ， Valine：
本文字数： 6.1k 阅读时长 ≈ 6 分钟

定义

第一章算法综述

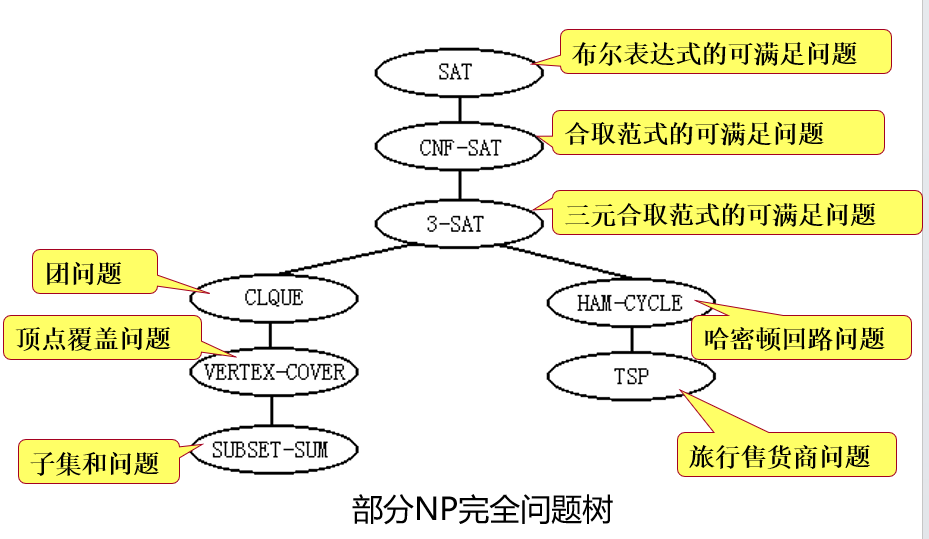
题1：NP问题，NPC问题

解析：C

  • NP问题：
  1. 无法在多项式时间内解决
  2. 但是已知一个可能的答案的话可以在多项式时间内验证

  • NPC问题：

    任何NP问题都可以规约成一个NPC问题

  • NP难问题

    相对于NP问题不仅无法在多项式时间内解决，也无法在多项式时间内验证

题2：NPC问题举例

第二章递归分支

题1：线性时间选择

线性时间选择问题采用拟中位数来作为划分的基准元素，可以在最坏情况下用\(O(n)\)时间完成选择任务 (正确)

解析：

通过select算法

第三章动态规划

题1：动态规划与贪心区别

题2：动态规划算法基本步骤

解析：

ADCB

第四章贪心

题1：用贪心能找到最优解的和不能找到最优解

解析

  • 贪心：
    1. 可以拆分的背包问题，如背包，最优装载
    2. 图论中单源最短路（dijkstra和floyd），最小生成树（prim和krusal），哈夫曼编码
    3. 活动安排
  • 非贪心
    1. 不可拆分的背包问题，如0-1背包，完全背包，最少硬币找零
    2. 多机调度
    3. 凸多边形剖分

第六章分支限界

题1

分支限界法中，每个活节点有多次机会成为拓展节点 （错误）

解析：分支限界法(BFS)每个活节点只有一次机会成为拓展节点，每次将所有孩子压入堆栈；回溯每个活节点有多次机会成为拓展节点，每次只将1个孩子压入堆栈

题2：分支限界法和回溯法的异同

  • 异：

    1. 节点拓展

      分支限界法每个节点值拓展1次，一次生成所有节点入队；回溯法每个节点可能拓展多次，一次只生成1个节点入队

    2. 存储结构：

      分支限界用的是队列，回溯用的是堆栈

    3. 搜索策略

      分支限界是BFS，回溯是DFS

  • 同：

    1. 都可以求最优解和解向量
    2. 都需要可行性剪枝，都可以通过限界函数优化
    3. 时间复杂度都是指数级

第七章随机化过程

题1：快速排序中引入随机化过程目的

解析：C

  1. 改善的是最坏，平均就是\(O(nlogn)\)

计算

第三章动态规划

题1：如何快速计算0-1背包

  1. 列三列，分别是物品，对应价值，对应重量
  2. 再列最后一列表示背包的容量
  3. 从上往下填充

视频讲解

题2：最长上升子序列

解析：

  1. dp[i]：必须以i结尾的最长上升子序列的长度

  2. 动归方程：

    对于当前以j结尾，从j往前扫描，选择比a[j]小的a[k]，且要满足前面条件中最大的

  3. dp数组

题3：最大子段和

解析：

  • 穷举

    子段长度从1到n，长度为1的子段有n个，长度为2的子段有n-1个，……长度为n的子段有1个，总共有\(\frac{(n + 1) * n}{2}\)，时间复杂度是\(O(n^2)\)

  • 分支，类似快排，递归方程式\(T(n) = 2T(n/2) + n\)，时间复杂度是\(O(nlogn)\)

  • 动规，dp[i]表示以i结尾的子段的最大子段和，\(dp[i] = max(dp[j - 1], a[j])， 1 \leq j \leq n\)，时间复杂度是\(O(n)\)

注：子序列和子段动规的区别在于，子序列是可以间断的，所以上一级的最优值可以从1~j-1里面取，子段是连续的，所以上一级只能取j-1

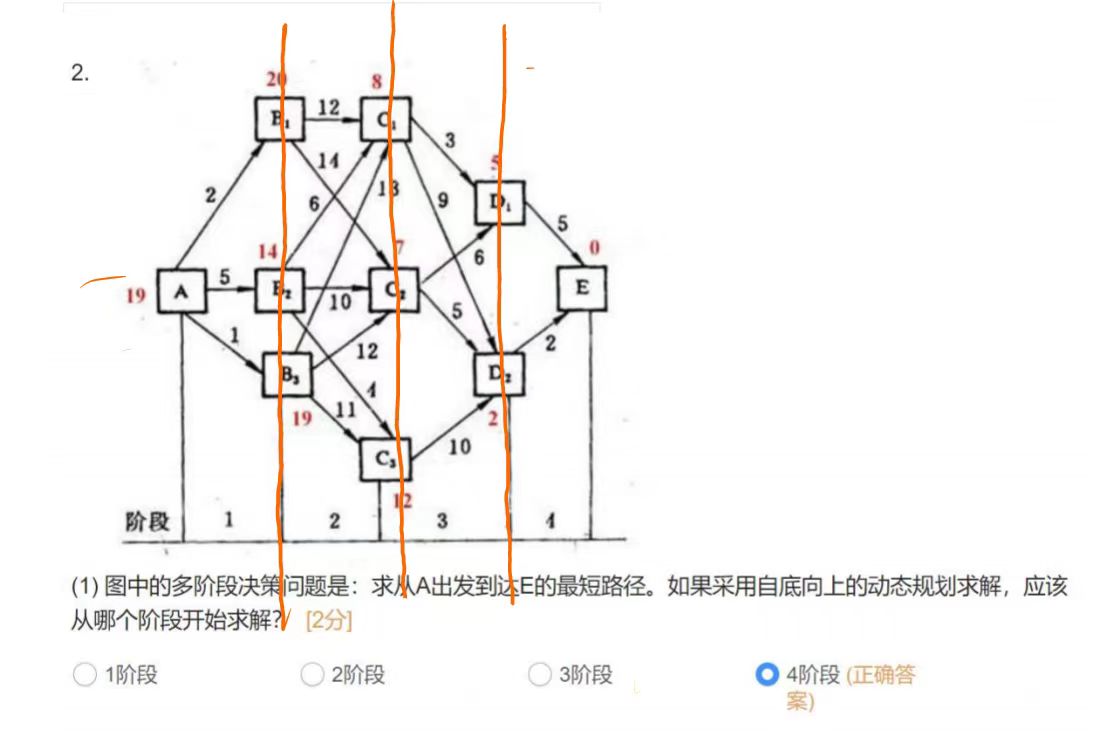
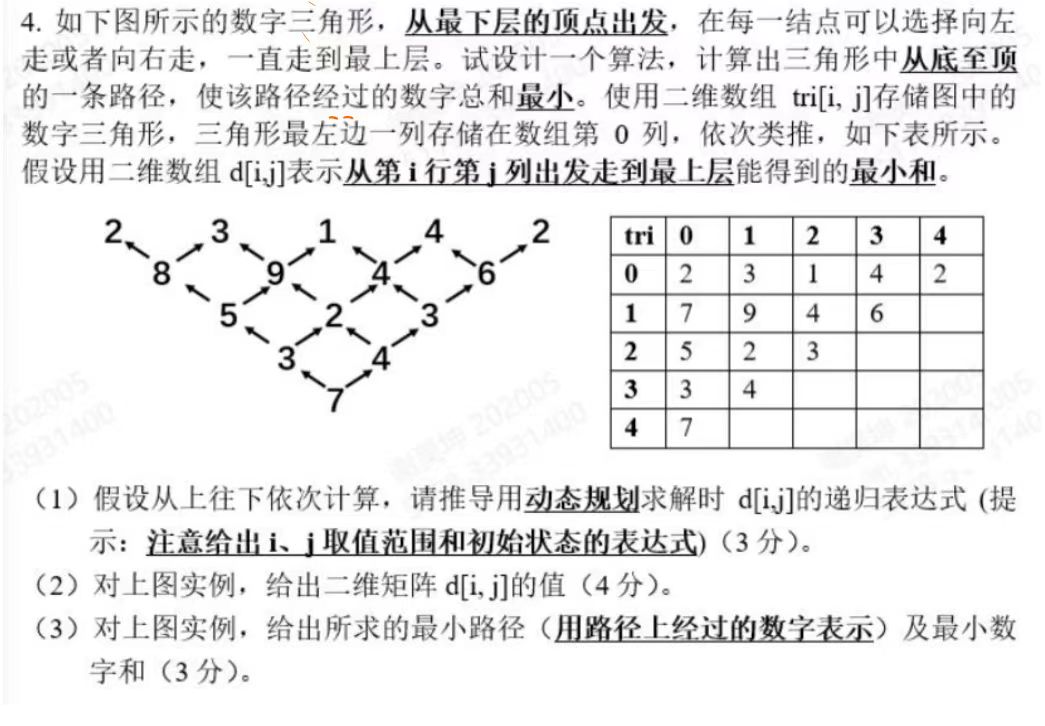
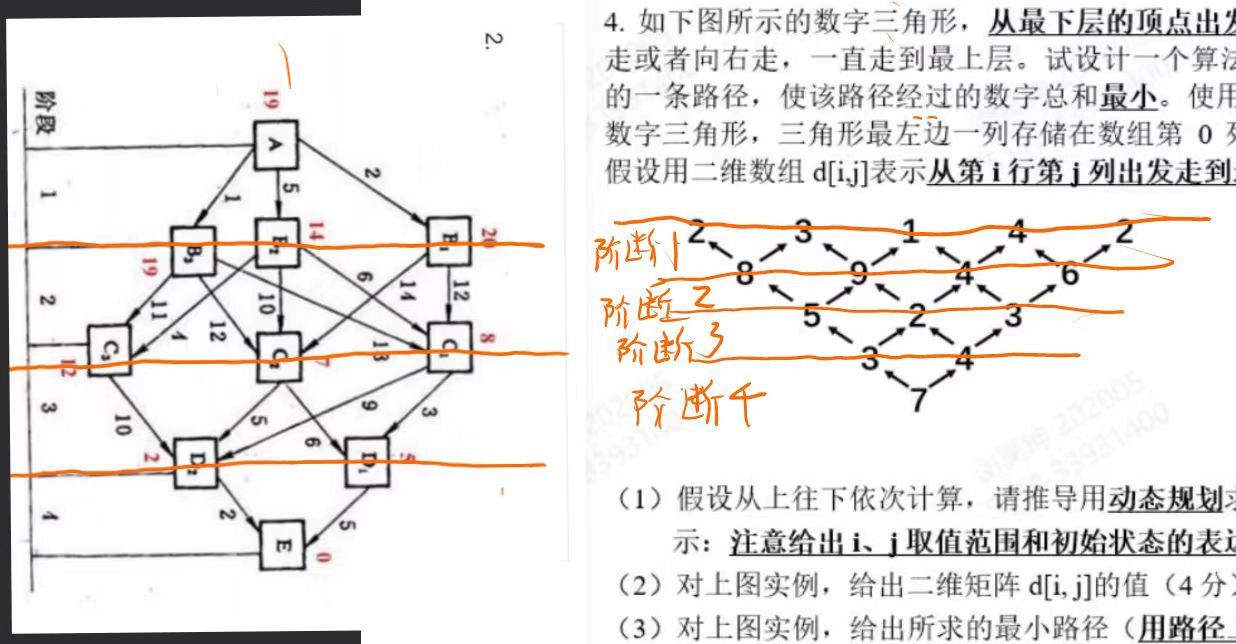
题4：单源最短路

4.1

4.2

解析：上面两道题其实是一种题，把第一个图片旋转90度就是第二张图

图形特点是上一层节点与下一层每个节点都有关系

第七章随机化过程

题1：蒙特卡洛算法计算调用次数

编程

第二章分治

二分查找

主要思路：

1 定好左端点与右端点

2 比较由左端点与右端点得出的中间值与目标值关系，根据此关系修改左端点或右端点，得出新的中间值，重复上述过程

易错点：

1 区间的关系：如果是全闭区间，则在while中应该是left<=right，因为[1,1]是合法区间，

而如果是左闭右开区间，则在while中应该是left<right,因为[1,1)是不合法区间

2 左右端点的修改：如果是全闭区间，修改左端点则是middle+1，修改右端点则是middle-1，因为已知middle不符合要求，则要在新区间中排除

而如果是左开右闭区间，已知middle不是合法区间，所以左端点修改是middle+1，而右端点修改是middle

全闭区间代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int search(int* nums, int numsSize, int target){
    int left = 0, right = numsSize - 1;    //小技巧，用下标值，不用定义指针，与出入的数组首地址组成指针
    int ret = -1;
    while(left <= right) {                //易错一
        int middle = (right + left) / 2;
        if(nums[middle] < target) {
            //printf("%d\n",nums[middle]);
            left = middle + 1;            //易错二
        }
        else if(nums[middle] > target) {
            //printf("%d\n",nums[middle]);
            right = middle - 1;
        }
        else {
            //printf("%d\n",ret);
            ret = middle;
            break;                
        }
    }
    return ret;
}

左开右闭区间代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int search(int* nums, int numsSize, int target){
    int left = 0, right = numsSize;
    int ret = -1;
    while(left < right) {        //易错一
        int middle = (left + right) / 2;
        if(nums[middle] < target) {
            left = middle + 1;    
        }
        else if(nums[middle] > target) {
            right = middle;    //易错二
        }
        else {
            ret = middle;
            break;
        }
    }
    return ret;
}

归并排序

解析：

利用归并排序，当两个部分合并的时候，因为左右两个部分都已经排好序，所以如果右半部分的当前指针指向的数比左半部分当前指针指向的数小，那么左半部分当前位置到左半部分末尾的数都可以和右半部分当前指针指向的数组成逆序对

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
int count = 0;
public static void backtrack(int[] data, int start, int end) {
    if(start == end) {
        return;
    }
    int mid = (start + end) / 2;
    backtrack(data, start, mid);
    backtrack(data, mid + 1, end);
    int[] tmp = new int[end - start + 1];
    int pl = start;
    int pr = mid + 1;
    int total = 0;
    int last = end - start;
    while(pr <= mid && pr <= end) {
        if(left[pl] < right[pr]) {
            tmp[total] = left[pl];
            total++;
            pl++;
        } else {
            tmp[total] = rigth[pr];
            pr++;
            count += (mid - pl + 1);	//计算当前所有逆序对的数量
        }
    }
    if(pl != mid) copy(left[pl, mid], tmp[total, last]);
    if(pr != end) copy(right[pr, mid], tmp[total, last]);
    copy(tmp[0, last], data[start, end]);
    return;
}

归并排序原始代码

记得先左右部分分别递归然后归并到一个tmp数组最后用这个tmp数组覆盖原数组对应部分就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public static void mergeSort(int[] data, int start, int end) {
    // 如果当前数组只有1个元素，直接返回
    if(start == end) {
        return;
    }
    int[] tmp = new int[start - end + 1];
    int mid = (start + end) / 2;
    mergeSort(data, start, mid);	// 对左半部分继续递归
    mergeSort(data, mid + 1, end);	// 对右半部分进行递归
    int p = start;	//左半部分的第一个
    int q = mid + 1; 	//右半部分的第一个
    int r = 0;
    int last = start - end;
    // 下面这个while是归并过程
    while(p <= mid && q <= end) {
        if(data[p] < data[q]) {
            data[r++] = data[q++];
        } else {
            data[r++] = data[p++];
        }
    }
    // 如果左半部分还没有遍历完，将剩下的全部复制到tmp数组里
    if(p < mid) {
        copy(data, p, mid, tmp, r, last);
    } 
    // 如果右半部分还没有遍历完，将剩下的全部复制到tmp数组里
    if(q < end) {
        copy(data, q, end, tmp, r, last);
    }
    copy(tmp, 0, last, data, start, end);
}

第三章动态规划

最长公共子序列

计算出dp[word1.length][word2.length]后，修改次数就是word1.length + word2.length - 2 * dp[word1.length][word2.length]

最长公共子序列原始代码

  1. dp[i][j]表示字符串x以i结尾，字符串y以j结尾的时候最长公共子序列

  2. 动规方程

  3. 动规矩阵中列表示字符串x，行表示字符串y

  4. 先固定x的结尾，移动y的结尾，分为三种：相同，去掉x结尾更大，去掉y结尾更大

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public static void lcsLength(int m, int n, char[] x, char[] y, int[][] c, int[][] b) {
    // Initialize DP tables
    for (int i = 0; i <= m; i++) {	//列代表字符串X
        c[i][0] = 0;
    }
    for (int i = 0; i <= n; i++) {	//行代表字符串Y
        c[0][i] = 0;
    }

    // 控制变量法，先固定x的结尾，移动y的结尾
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (x[i] == y[j]) {	// 如果末尾相同
                c[i][j] = c[i - 1][j - 1] + 1;	
                b[i][j] = 1;
            } else if (c[i - 1][j] >= c[i][j - 1]) {	//如果末尾不同且去x尾更长
                c[i][j] = c[i - 1][j];
                b[i][j] = 2;
            } else {	//如果末尾相同且去y尾更长
                c[i][j] = c[i][j - 1];
                b[i][j] = 3;
            }
        }
    }
}

第四章贪心

背包

原始背包代码

  1. 计算性价比，根据性价比重新排序
  2. 循环遍历重新排序的物品，如果当前物品放不下就break，然后按比例放入；如果放得下就加上当前物品价值，背包容量也减去相应物品重量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
  private void sort(int n, float[] v, float[] w) {
       // 假设已经实现排序算法
       // 这里使用Arrays.sort()进行排序
       float[][] items = new float[n][2];
       for (int i = 0; i < n; i++) {
           items[i][0] = v[i];
           items[i][1] = w[i];
       }
       Arrays.sort(items, (a, b) -> Float.compare(b[0] / b[1], a[0] / a[1]));

       for (int i = 0; i < n; i++) {
           v[i] = items[i][0];
           w[i] = items[i][1];
       }
   }
public void knapsack(int n, float M, float[] v, float[] w, float[] x) {
       sort(n, v, w);
       for (int i = 0; i < n; i++) {
           x[i] = 0;
       }
       float c = M;
       int i;
       for (i = 0; i < n; i++) {
           if (w[i] > c) {
               break;
           }
           x[i] = 1;
           c -= w[i];
       }
       if (i < n) {
           x[i] = c / w[i]; // 最后装入部分物品
       }
   }

第五章回溯

最大团

原始代码

  1. 递归终点是叶子节点，如果当前最优值值比之前的最优值更优，就用当前解向量与最优值覆盖之前的
  2. 可行性剪枝的标准是将当前节点i与现在团里的每个元素是否都有关系
  3. 限界剪枝的标准是如果放弃当前的元素，那么剩下的元素加上当前团里的元素是否大于等于最优值，如果还比最优值小就不用搜了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int n = 0;
int bestn;
int[] x = new int[max];
int[] bestx = new int[max];
public static void backtrack(int i) {	//i表示当前是第几层
    if(i == n) {
        if(n > bestn) {
            for(int i = 0; i < size; i++) bestx[i] = x[i];
            bestn = n;
        }
        return;
    }
    
    boolean ok = true;
    for(int j = 1; j < i; j++) {
        if(x[j] == 1 && a[j][i] == NOEDGE) {	//x[j] == 1表示当前节点在最大团中，a[j][i]表示在矩阵表示中i和j两个顶点没有联系
            ok = false;
            break;
        }
    }
    if(ok == true) {
        x[i] = 1;
        n++;
        backtrack(i + 1);
        x[i] = 0;
        n--;
    } 
    
    if(n + total - i > bestn) {
        backtrack(i + 1);
    } 
}