第二章-递归与分治

主定理解析

结论

分析

递归公式通用形式

\(T(n) = aT(\frac{n}{b}) + O(n^d)\)

最后的时间复杂度和这a, b ,d几个参数有关。

把递归问题每一层的问题数目，计算量都一一列出，可以得到如下公式

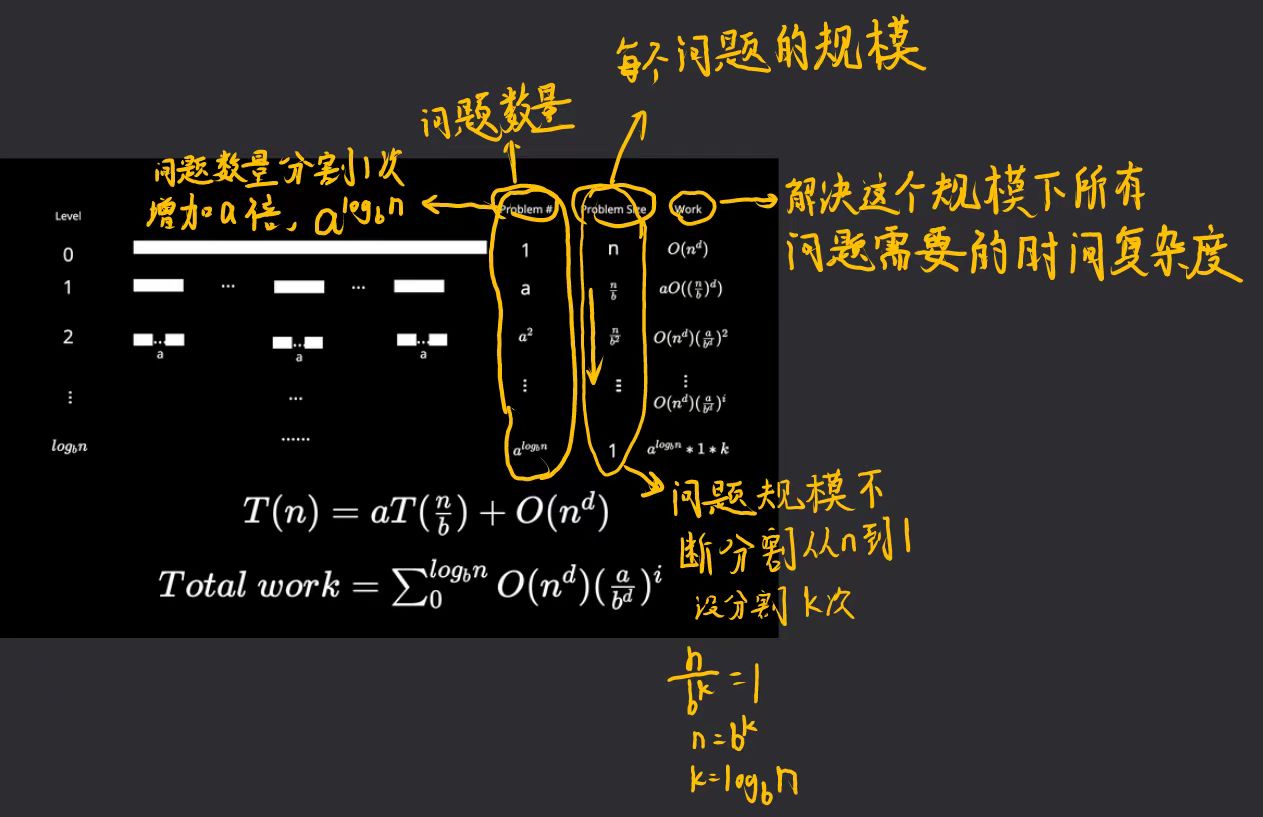
最终的总规模是等比数列，因为初始问题规模n是固定的，d是规定的，将\(O(n^d)\)看作常数，公比是\(\frac{a}{b^d}\)

• 情况一：公比小于1

  时间复杂度由第一项确定

  

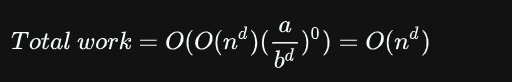
• 情况二：公比大于1

  时间复杂度由最后一项确定

  

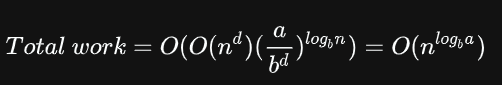
​ 化简过程：
​

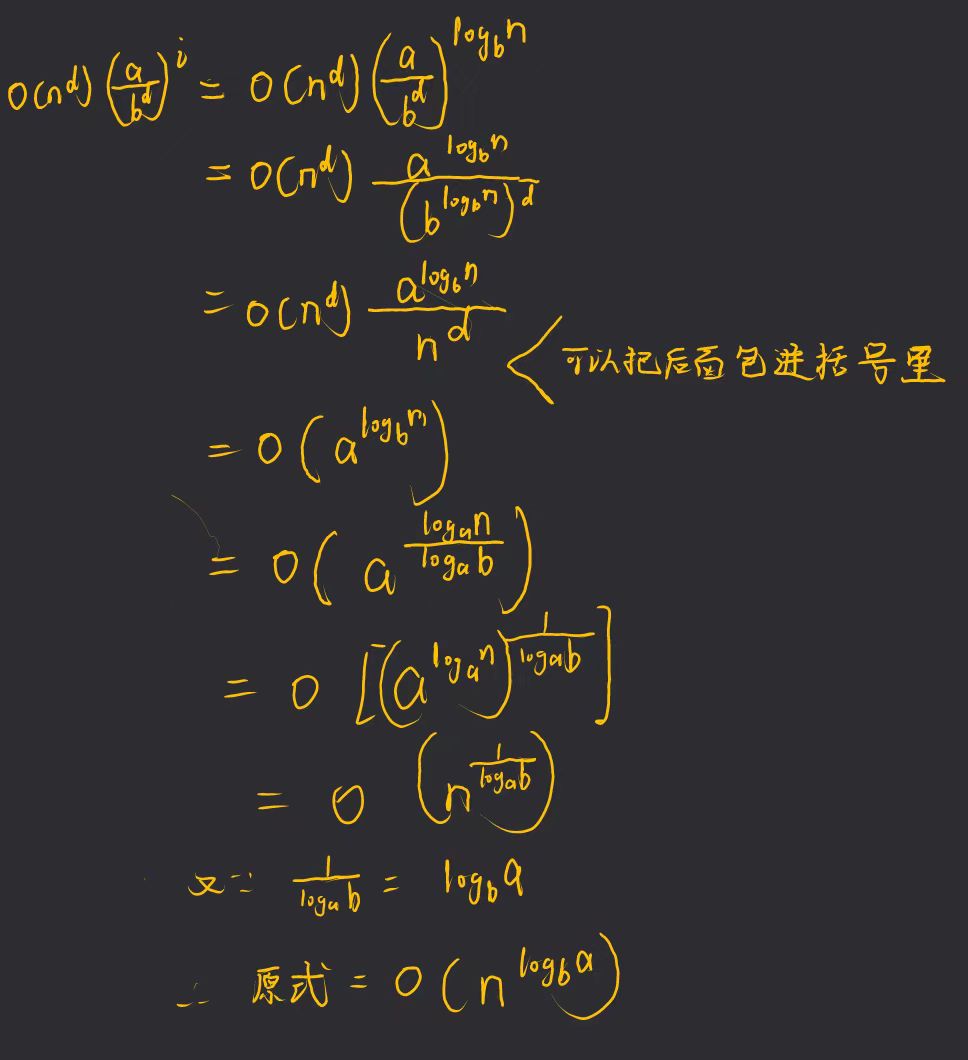
• 公比等于1

  

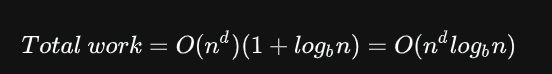
二分搜索

大整数乘法

Strassen矩阵乘法

棋盘覆盖

归并排序

思想

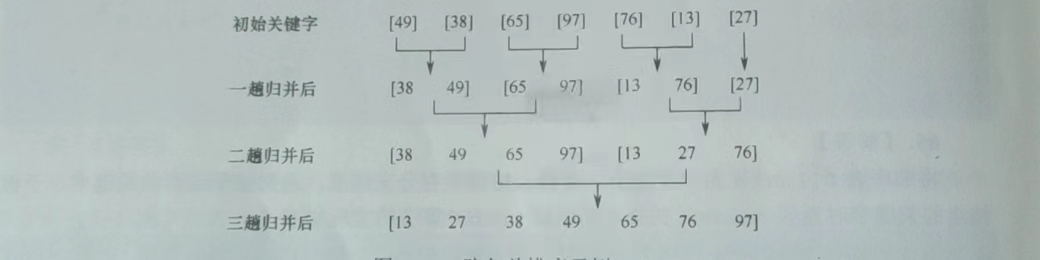
1. “分”：分割成小序列，一直分割直到只有1个元素，然后回退
2. 治：小序列两个两个合并成大序列

• 开一个辅助数组B
• 这时待排数组为空，利用两个指针p和q分别指向待归并的两个数组的起点，第三个指针r指向辅助数组，将p和q中较大的放入辅助数组B，比如如果是p，然后移动p指针，另一个指针q保持不变
• 如果其中一个指针移动的位置超过了原来对应待归并的数组的范围，将剩下一个数组里元素全部拷贝回待排数组

代码

public static void mergeSort(int[] data, int start, int end) {
    // 如果当前数组只有1个元素，直接返回
    if(start == end) {
        return;
    }
    int[] tmp = new int[start - end + 1];
    int mid = (start + end) / 2;
    mergeSort(data, start, mid);	// 对左半部分继续递归
    mergeSort(data, mid + 1, end);	// 对右半部分进行递归
    int p = start;	//左半部分的第一个
    int q = mid + 1; 	//右半部分的第一个
    int r = 0;
    int last = start - end;
    // 下面这个while是归并过程
    while(p <= mid && q <= end) {
        if(data[p] < data[q]) {
            data[r++] = data[q++];
        } else {
            data[r++] = data[p++];
        }
    }
    // 如果左半部分还没有遍历完，将剩下的全部复制到tmp数组里
    if(p < mid) {
        copy(data, p, mid, tmp, r, last);
    } 
    // 如果右半部分还没有遍历完，将剩下的全部复制到tmp数组里
    if(q < end) {
        copy(data, q, end, tmp, r, last);
    }
    copy(tmp, 0, last, data, start, end);
}

快速排序

线性时间选择

问题描述

给定线性序集中n个元素和一个正数k，1 ≤ k ≤ n，要求找出这n个元素中第k小的元素

RandomizedSelect算法

算法思路

1. 初始化：给定数组a，范围从p到r，以及要查找的第k小的元素。

2. 基线条件：如果数组的长度小于等于k，则说明第k小的元素一定在这个数组中。

3. 随机选择枢纽：在数组a[p:r]中随机选择一个元素i。

4. 划分数组：根据枢纽i的值，将数组划分为两个子数组：

   • a[p:j]：包含小于i的元素。
   • a[j+1:r]：包含大于或等于i的元素。

5. 递归查找：

   • 如果左侧小于等于枢纽的子数组的长度小于k，则在右侧大于枢纽的子数组a[j+1:r]中递归查找第k 小的元素。
   • 如果左侧小于等于枢纽的子数组的长度大于等于k，则在左侧小于等于枢纽的子数组a[p:j]中递归查找第k - (j - start + 1)小的元素。

6. 结束条件：当子数组的长度减少到1时，即p = r，此时的元素就是第k小的元素。

举例：

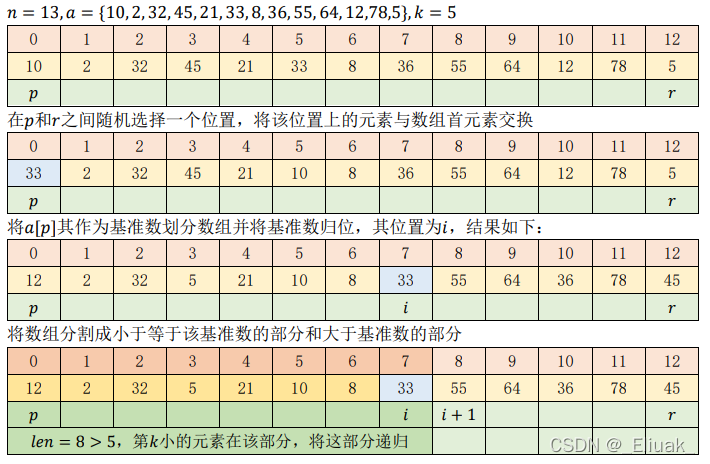
代码

public static int partion(int[] data, int k, int start, int end) {
    if(start == end) {
        return start;
    }

    int pivot = data[k];
    int p = start;
    int q = end;
    swap(data[start], pivot);
    while(p < q) {
        while(data[q] > pivot) q--;
        data[p] = data[q];
        while(data[p] <= pivot) p++;
        data[q] = data[p];
    }
    data[p] = pivot;
    if(p - start + 1 >= k) {
        int target = partion(data, k, start, p);
    } else {
        int target = partion(data, k - (p - start + 1), p + 1, end);
    }
    return target;
}

时间复杂度分析

Select算法

算法思路

1. 分组：将原数组分成 \(\lceil \frac{n}{5} \rceil\) 组，每组包含5个元素。如果数组的总元素数不能被5整除，最后一个组的元素数将小于5。

2. 每组排序：对每组的5个元素进行排序。

3. 找每组中位数：在每组排序后的元素中，找到每组的中位数。如果组内的元素个数是奇数，则中位数是中间的元素；如果是偶数，则中位数是中间两个元素中较大的那个。

4. 递归找到基准：将所有组的中位数组合起来，形成一个新数组。如果这个新数组的元素个数是奇数，直接取中间的元素作为基准 \(x\)；如果是偶数，则取中间两个元素中较大的那个作为基准 \(x\)。这个过程可以通过递归调用快速选择算法来实现。

5. 划分数组：根据基准 \(x\) 的值，将原数组划分为两部分：

   • 小于 \(x\) 的元素。
   • 大于或等于 \(x\) 的元素。

6. 递归处理：

   • 如果要查找的第 \(k\) 小的元素在基准 \(x\) 的左侧，则在左侧的子数组中递归查找第 \(k\) 小的元素。
   • 如果 \(k\) 大于基准 \(x\) 在数组中的位置（即 \(k > \lceil \frac{n}{2} \rceil\)），则在右侧的子数组中递归查找第 \(k - \lceil \frac{n}{2} \rceil\) 小的元素。

7. 结束条件：当子数组的长度减少到1时，即找到了第 \(k\) 小的元素。

这种“中位数的中位数”算法可以减少算法的最坏情况时间复杂度，使其在最坏情况下也能保持较好的性能。

举例：

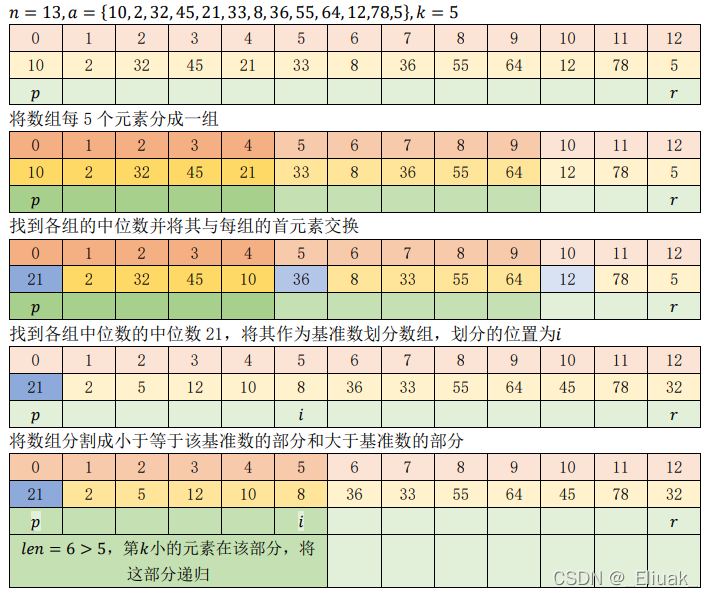
时间复杂度

循环赛日程表

伯努利错配信件

最接近点对