地图上有 N 个目标,用整数 Xi,Yi ,
表示目标在地图上的位置,每个目标都有一个价值 Wi 。
注意:不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含
R×R个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和
x,y 轴平行。
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
## 输入格式
第一行输入正整数 N 和 R
,分别代表地图上的目标数目和正方形包含的横纵位置数量,数据用空格隔开。
接下来 N 行,每行输入一组数据,每组数据包括三个整数 Xi,Yi,Wi , ,
,分别代表目标的 x 坐标,y 坐标和价值,数据用空格隔开。
## 输出格式
输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
## 数据范围
\(0≤R≤10^9\) \(0<N≤100000\) \(0≤Xi,Yi≤50000\) \(0≤Wi≤10000\)
## 输入样例:
## 输出样例:
分析
首先讲解下什么是二维前缀和
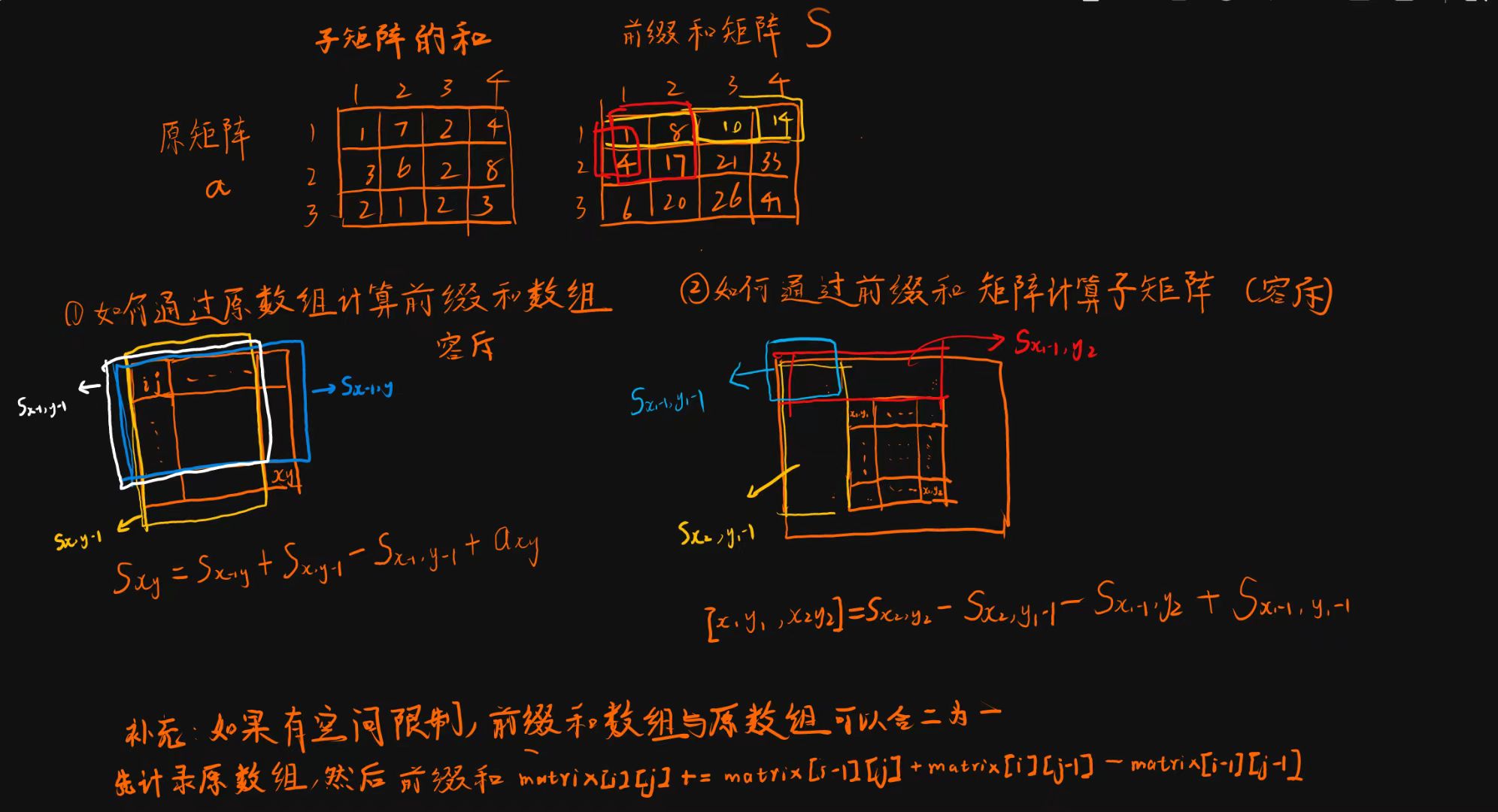
但是本题的特殊之处在于给的目标是在交叉点上,而上面给的是第几个矩阵
解决方法:平移坐标系,原来在坐标轴上的目标就变成了在坐标轴内的目标,进一步就是变成了和原来一样的第几个小正方形

所以先将目标的value填充到对应的方格中,然后计算value的前缀和矩阵,最后利用计算出的前缀和矩阵,通过移动覆盖面积的小方形,以其右下角为基准遍历整个矩阵,计算覆盖面积的最大值
前缀和的灵魂就是将本来时间复杂度\(O(n)\)甚至\(O(n^2)\)的循环遍历求和变成\(O(1)\)
注意:
1 题目中一个坐标处可能有多个目标
2 如果火力覆盖面积比最大的5000还大,那就可以不用遍历直接得到答案
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| import java.time.chrono.MinguoChronology;
import java.util.Scanner;
public class Main {
static int MAXSIZE = 5010;
static int[][] matrix = new int[MAXSIZE][MAXSIZE];
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int r = scan.nextInt();
r = Math.min(r, 5001);
int max_x = r;
int max_y = r;
for(int i = 0; i < n; i++) {
int x = scan.nextInt();
int y = scan.nextInt();
matrix[x + 1][y + 1] += scan.nextInt();
max_x = Math.max(x + 1, max_x);
max_y = Math.max(y + 1, max_y);
}
for(int i = 1; i <= max_x; i++) {
for(int j = 1; j <= max_y; j++) {
matrix[i][j] += matrix[i - 1][j] + matrix[i][j - 1] - matrix[i - 1][j - 1];
}
}
int maxValue = 0;
for(int i = r; i <= max_x; i++) {
for(int j = r; j <= max_y; j++) {
int value = matrix[i][j] - matrix[i - r][j] - matrix[i][j - r] + matrix[i - r][j - r];
if(value > maxValue) {
maxValue = value;
}
}
}
System.out.println(maxValue);
scan.close();
}
}
|

