线性表
定义：
类型相同的数据元素
长度有限
逻辑结构
题型一：什么是线性表
微信图片_20231217105307
线性表的顺序表示，又叫顺序表
定义：
逻辑相邻，物理也相邻
与数组区别在于线性表是从下标1开始存储，数组是从0开始
举例：顺序存储线性表的特点：随机存取，含义是线性表可以直接访问指定地址元素，且时间复杂度为O(1)
微信图片_20231217140802
基本操作
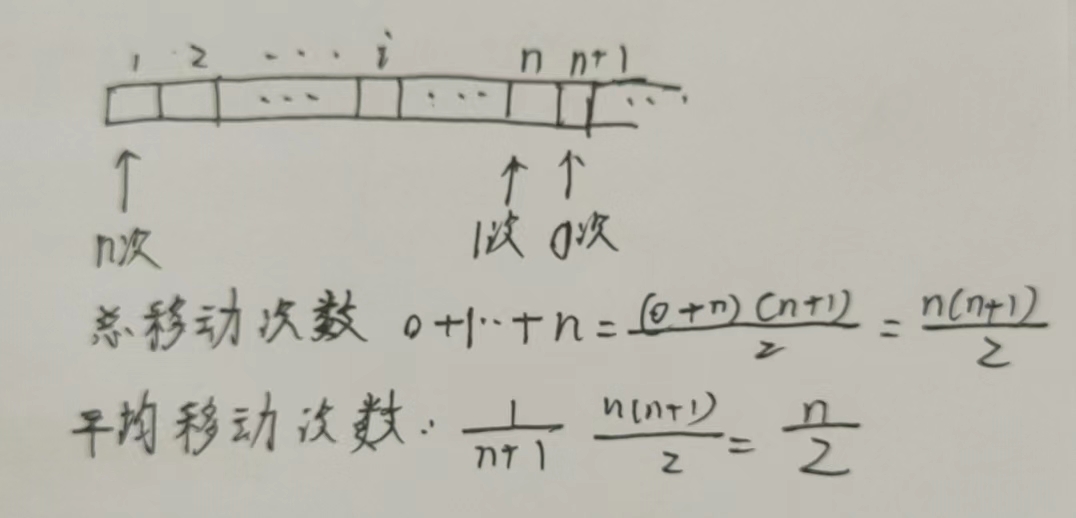
在第i个位置插入新元素e(插入位置可以从1到L.length
+ 1)
主要思路：从最后一个起到第i个将所有元素往后移动一位，这样位置i就空出来可以放元素了
\(平均次数：\frac{n}{2}\)
微信图片_20231217140039
\(时间复杂度O(n)\)
1
2
3
4
5
6
7
8
9
10
| bool ListInsert(SqList &L, int i, Elemtype e) {
if(i < 1 || i > L.length + 1) {
return false;
}
for(int j = L.length; L >= i; i++) {
L.data[j + 1] = L.data[j];
}
L.data[i] = e;
return true;
}
|
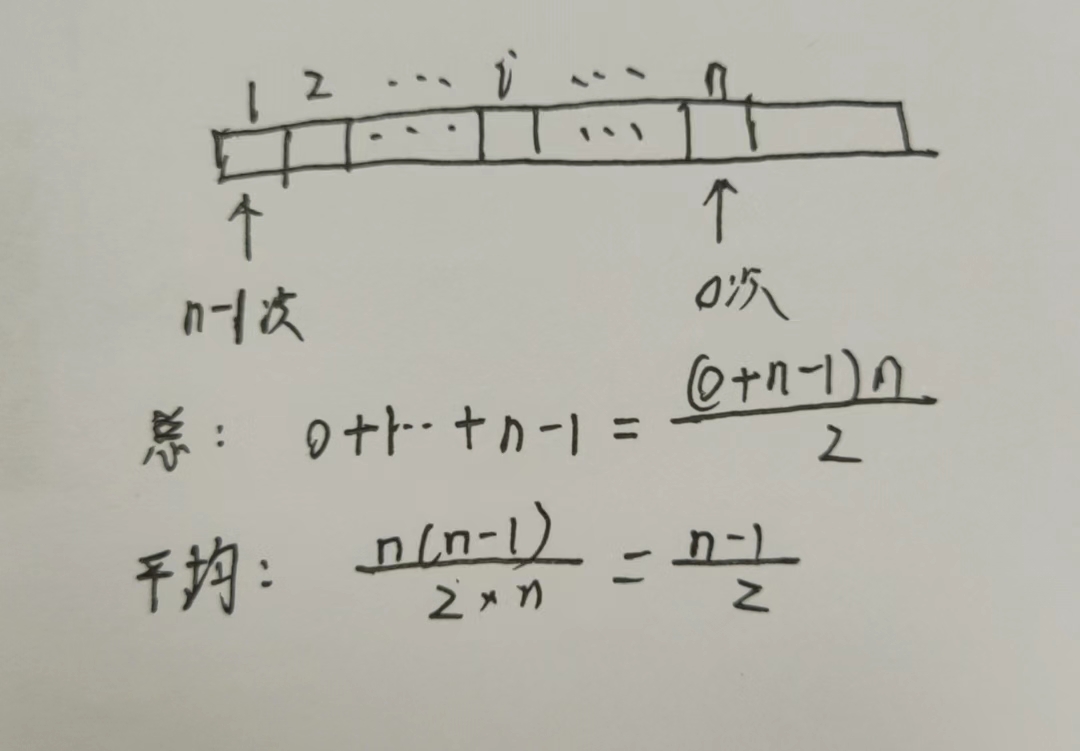
删除第i个位置元素，删除位置1到L.length
主要思路：通过将从i
+ 1个位置起元素一起向前移动一位,覆盖前一位元素实现
\(移动节点平均次数\frac{n-1}{2}\)
微信图片_20231217140458
\(时间复杂度O(n)\)
1
2
3
4
5
| bool ListDelete(SqList &L, int i, Elemtype &e) {
for(int j = i; j < L.length; j++) {
L.data[j] = L.data[j + 1];
}
}
|
查找值是i的元素：就是遍历整个数组查找
线性表的链式表示：
头节点和头指针
头节点：叫头结点的就是虚拟头节点
头指针：头指针始终指向第一个节点，如果有头节点就指向头节点，如果没有就指向链表的第一个节点
单链表
头插法
1
新节点的尾指针指向虚拟头节点的next
2
虚拟头节点的next再指向新节点
1
2
| newNode->next = L->next;
L->next = newNode;
|
尾插法
1定义一个额外的尾指针
2 先把尾指针的next指向新节点
3 再移动尾指针指向新节点
4最后把尾指针的next放空
1
2
| rear->next = newNode;
rear = newNode;
|
按序号查找：注意节点序号从1开始(因为链表也是线性表，线性表就是从1开始)
，指针p一次往后移动1次，移动i-1次，最终指向的位置就是序号i的节点
1
2
3
4
5
6
7
| p = L->next;
int j = 1;
while(p && j < i) {
p = p->next;
j++;
}
return p;
|
按值查找
在位置i插入节点
先查找插入位置前驱节点，利用前面写好的按序号查找方法
在将新节点的next指向原来序号i的节点，序号i-1的next指向新节点
1
2
3
| LNode *before = GetElem(LinkList L, i-1);
newNode->next = before->next;
before->next = newNode;
|
删除序号是i的节点
利用前面查找节点查找到节点i-1
用临时指针指向节点i
节点i-1的next直接指向i的next
free掉节点i
1
2
3
4
| LNode *before = GetElem(LinkList L, i);
LNode *tmp = before->next;
before->next = tmp->next;
free(tmp);
|
求表长
双链表
在指定节点p之后插入节点s(顺序不唯一，但一定要注意操作过程不能把原来的后继节点位置中途搞丢)
1
2
3
4
5
6
|
s->next = p->next;
p->next->prior = s;
s->prior = p;
p->next = s;
|
删除节点p的后继节点q
1
2
3
| p->next = q->next;
q->next->priror = p;
free(q);
|
循环链表
循环单链表：尾节点的next不是NULL，而指向头节点
举个例子
微信图片_20231217160038
删除后还要判断链表是否为空，如果为空(临时指针和尾指针指向同一个节点，就要修改尾指针)
####循环双链表
静态链表：结构体数组的数据域data里存数据，指针域里存下一个节点的地址，不过这个地址是结构体数组里unsigned
int类型的下标