Pilot's Blog
0%

Acwing95-费解的开关

发表于 更新于 分类于 ， ， Valine：
本文字数： 3.4k 阅读时长 ≈ 3 分钟

题目

你玩过“拉灯”游戏吗？

2525 盏灯排成一个 5×55×5 的方形。

每一个灯都有一个开关，游戏者可以改变它的状态。

每一步，游戏者可以改变某一个灯的状态。

游戏者改变一个灯的状态会产生连锁反应：和这个灯上下左右相邻的灯也要相应地改变其状态。

我们用数字 11 表示一盏开着的灯，用数字 00 表示关着的灯。

下面这种状态

1
2
3
4
5
10111
01101
10111
10000
11011

在改变了最左上角的灯的状态后将变成：

1
2
3
4
5
01111
11101
10111
10000
11011

再改变它正中间的灯后状态将变成：

1
2
3
4
5
01111
11001
11001
10100
11011

给定一些游戏的初始状态，编写程序判断游戏者是否可能在 66 步以内使所有的灯都变亮。

输入格式

第一行输入正整数 n�，代表数据中共有 n� 个待解决的游戏初始状态。

以下若干行数据分为 n� 组，每组数据有 55 行，每行 55 个字符。

每组数据描述了一个游戏的初始状态。

各组数据间用一个空行分隔。

输出格式

一共输出 n� 行数据，每行有一个小于等于 66 的整数，它表示对于输入数据中对应的游戏状态最少需要几步才能使所有灯变亮。

对于某一个游戏初始状态，若 66 步以内无法使所有灯变亮，则输出 −1−1。

数据范围

0<n≤5000<�≤500

输入样例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
3
00111
01011
10001
11010
11100

11101
11101
11110
11111
11111

01111
11111
11111
11111
11111

输出样例：

1
2
3
3
2
-1

分析

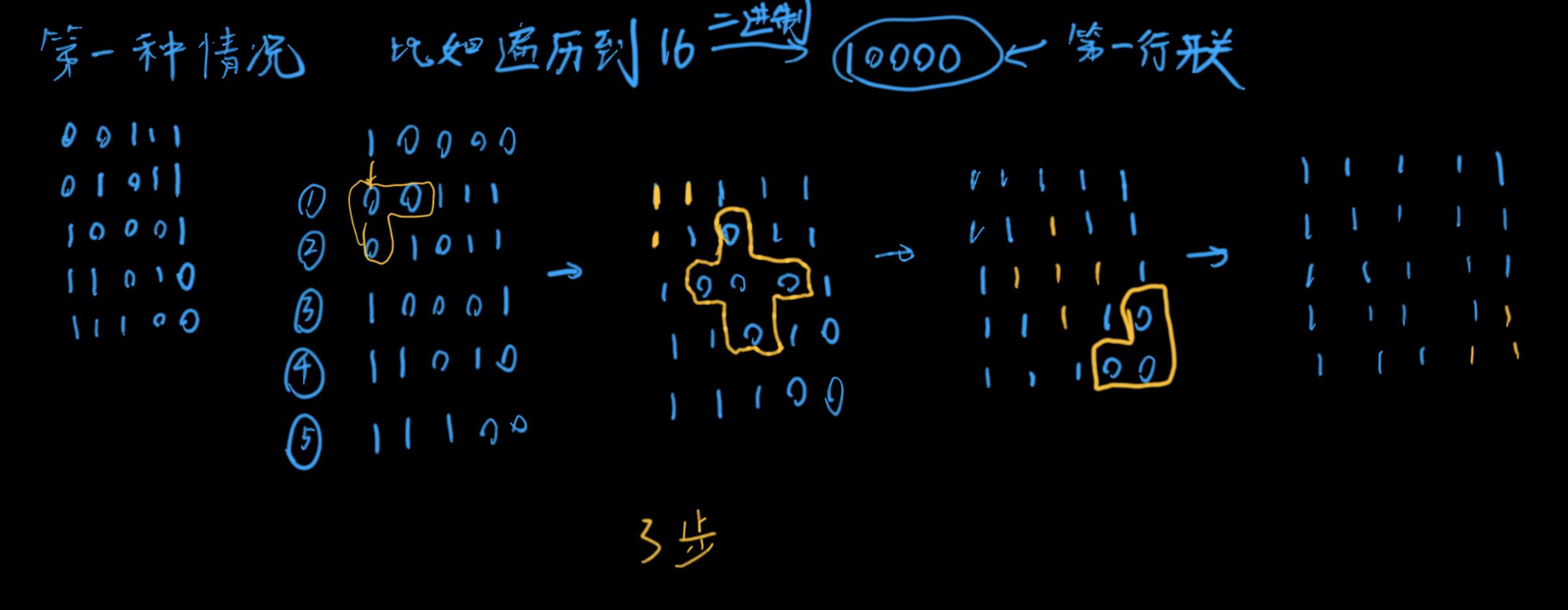
本题关键在于如何枚举

每一行灯的情况由上一行决定，上一行的暗灯由下一行的开关点亮，点亮之后就要改变对应的上下左右其他灯

枚举的是第一行开关闭合与否的情况，与灯的亮暗无关，每一个开关有亮和暗两种情况，5个开关就\(2^5 =32\)种情况，当开关的情况定下来后，第一行的灯的亮暗也就确定了，之后几行的灯的亮暗也跟着确定

举例说明

c1736fb66ab0f65acd8923abc0e9ff9

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
import java.util.Arrays;
import java.util.Scanner;
public class Main {
	static char[][] matrix = new char[5][];
	static char[][] backUp = new char[5][];
	static void readMatrix(Scanner scan) {
		String tmp = scan.nextLine();
		for(int i = 0; i < 5; i++) {
			matrix[i] = scan.nextLine().toCharArray();
			backUp[i] = Arrays.copyOf(matrix[i], matrix[i].length);
		}
	}
	static void flip(int x, int y) {
		if(matrix[x][y] == '0') {
			matrix[x][y] = '1';
		} else {
			matrix[x][y] = '0';
		}
	}
	static void changeMatrix(int x, int y) {
		// 上
		if(x - 1 >= 0) flip(x - 1, y);
		// 左
		if(y - 1 >= 0) flip(x, y - 1);
		// 右
		if(y + 1 <= 4) flip(x, y + 1);
		// 下
		if(x + 1 <= 4) flip(x + 1, y);
		// 自个
		flip(x, y);
	}
	public static void main(String[] args) {
		Scanner scan = new Scanner(System.in);
		int n = scan.nextInt();
		// 一共要有n次读取
		int count = 0;
		for(int i = 0; i < n; i++) {
			// 读取每次的初始灯矩阵并保存备份
			readMatrix(scan);
//			System.out.println("初始化矩阵为：");
//			for(int j = 0; j < 5; j++) {
//				System.out.println(matrix[j]);
//			}
			int minChange = Integer.MAX_VALUE;
			// 遍历 32 种可能性
			for(int j = 0; j < 32; j++) {
				count = 0;
				// 将第一行的按法调整成对应的5位二进制
				String tmpString = String.format("%5s", Integer.toBinaryString(j)).replace(' ', '0');
//				System.out.format("第一行的开关状态为：%s\n", tmpString);
				// 第一行的按完后的状态
//				System.out.print("第一行现在状态：");
//				System.out.println(matrix[0]);
				for(int k = 0; k < 5; k++) {
					if(tmpString.charAt(k) == '1') {
						changeMatrix(0, k);
//						System.out.format("按下开关%d, 第一行现在状态 ", k + 1);
//						System.out.println(matrix[0]);
						count++;
					}
				}
//				System.out.println("开关按完后第一行现在的状态：");
//				System.out.println(matrix[0]);
				
	
				for(int a = 0; a < 4; a++) {
					for(int b = 0; b < 5; b++) {
						// 通过这一行确定下一行的开关，再根据这个开关看灯的亮暗
						if(matrix[a][b] == '0') {
							changeMatrix(a + 1, b);
							count++;
						}
					}
//					System.out.format("经过第%d行后的状态\n", a+1);
//					for(int c = 0; c < 5; c++) {
//						System.out.println(matrix[c]);
//					}
				}
				
				// 遍历第5行，看是不是都是1
				boolean flag = true;
				for(int k = 0; k < 5; k++) {
					if(matrix[4][k] == '0') {
						flag = false;
						break;
					}
				}
				
				if(flag) {
					minChange = Math.min(count, minChange);
				}
				
				// 将备份矩阵拷贝回原矩阵
				for(int a = 0; a < 5; a++) {
					matrix[a] = Arrays.copyOf(backUp[a], backUp[a].length);
				}
//				System.out.println("backUp数组是：");
//				for(int a = 0; a < 5; a++) {
//					System.out.println(backUp[a]);
//				}
			}
			if(minChange <= 6) System.out.println(minChange);
			else System.out.println(-1);
		}
	}
}

注：

深拷贝与浅拷贝，一个大坑，当时折腾了半天