矩阵连乘问题

问题描述

给定n个矩阵｛A1,A2,…,An｝，其中Ai与Ai+1是可乘的，i=1，2…，n-1。如何确定计算矩阵连乘积的计算次序，使得依此次序计算矩阵连乘积需要的数乘次数最少。

详细说明：

完全加括号的矩阵连乘积

定义

递归定义如下

计算乘法次数

视频讲解：矩阵连乘中乘法次数的计算

解决方案

穷举

时间复杂度分析：

视频讲解：穷举法计算矩阵连乘问题序列数时间复杂度分析

动态规划

状态转移方程

其中参数的含义：

视频讲解：动归解决矩阵连乘中转移方程推导与代码分析

代码

public class MatrixChain {
    public static void matrixChain(int[] p, int n, int[][] m, int[][] s) {
        // Initialize diagonal elements of m to 0
        for (int i = 1; i <= n; i++)
            m[i][i] = 0;

        for (int r = 2; r <= n; r++) {
            for (int i = 1; i <= n - r + 1; i++) {
                int j = i + r - 1;
                m[i][j] = m[i + 1][j] + p[i - 1] * p[i] * p[j];
                s[i][j] = i;
                for (int k = i + 1; k < j; k++) {
                    int t = m[i][k] + m[k + 1][j] + p[i - 1] * p[k] * p[j];
                    if (t < m[i][j]) {
                        m[i][j] = t;
                        s[i][j] = k;
                    }
                }
            }
        }
    }

备忘录

动归的优化，与纯动态规划区别在于，原来的动态规划的递归方向从底往上，比如上面是先计算出长度为i的矩阵，再利用得到的结果计算长度为i+1的矩阵

备忘录是利用递归从顶往下

代码

public static int lookupChain(int i, int j) {
    if (m[i][j] > 0) return m[i][j]; // 说明之前已经计算过，直接返回
    if (i == j) return 0; // 同1个矩阵
    
    int u = lookupChain(i, i) + lookupChain(i + 1, j) + p[i - 1] * p[i] * p[j];
    // 上面这步类似纯动归的初始化，分割线在i后面
    s[i][j] = i;
    for (int k = i + 1; k < j; k++) {
        int t = lookupChain(i, k) + lookupChain(k + 1, j) + p[i - 1] * p[k] * p[j];
        // 上面这个就是针对i, j序列找最小的m[i, j]
        if (t < u) {
            u = t;
            s[i][j] = k;
        }
    }
    m[i][j] = u;
    return u;
}

最长公共子序列

结构

注：公共子序列不一定连续

举例：X：A, B, C, C, D, E

Y:A, B, E, F

最长公共子序列：A, B, E

状态转移方程

c[ i ][ j ]记录序列和的最长公共子序列的长度

其中， Xi={x1,x2,…,xi}；Yj={y1,y2,…,yj}。当i=0或j=0时，空序列是Xi和Yj的最长公共子序列。故此时C[i][j]=0。

动归计算最长子序列长度

1
2
3

b[i][j] = 1 //情况一：X尾和Y尾相等
b[i][j] = 2 //情况二：去X尾更长
b[i][j] = 3 //情况三：去Y尾更长

代码

public static void lcsLength(int m, int n, char[] x, char[] y, int[][] c, int[][] b) {
    // Initialize DP tables
    for (int i = 0; i <= m; i++) {	//列代表字符串X
        c[i][0] = 0;
    }
    for (int i = 0; i <= n; i++) {	//行代表字符串Y
        c[0][i] = 0;
    }

    // 控制变量法，先固定x的结尾，移动y的结尾
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {
            if (x[i] == y[j]) {	// 如果末尾相同
                c[i][j] = c[i - 1][j - 1] + 1;	
                b[i][j] = 1;
            } else if (c[i - 1][j] >= c[i][j - 1]) {	//如果末尾不同且去x尾更长
                c[i][j] = c[i - 1][j];
                b[i][j] = 2;
            } else {	//如果末尾相同且去y尾更长
                c[i][j] = c[i][j - 1];
                b[i][j] = 3;
            }
        }
    }
}

根据上面得到的b矩阵构造最长公共子序列

public static void lcs(int i, int j, char[] x, int[][] b) {
    if (i == 0 || j == 0) return;
    if (b[i][j] == 1) {	// 情况一：结尾相等
        lcs(i - 1, j - 1, x, b);
        System.out.print(x[i - 1]);
    } else if (b[i][j] == 2) {	//情况而：结尾是y尾，y不动，去x尾
        lcs(i - 1, j, x, b);
    } else {	//情况三：结尾是x尾，y不动，去x尾
        lcs(i, j - 1, x, b);
    }
}

视频讲解：最长公共子序列的两种输出

最大子段和

定义

最大子段和要求是连续的

分治算法

时间复杂度分析（类似快排）

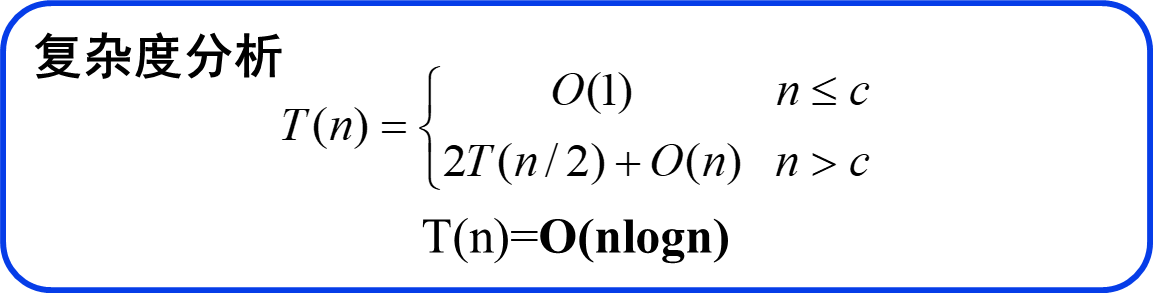
动归算法

状态转移方程：

定义数组b[ j ]表示含义为一定要取数组a[ j ]的情况下，能得到的最大子列和

b[ j ]=max{ b[ j-1 ]+a[ j ]，a[ j ]}，1≤j≤n

代码

public static int maxSum(int n, int[] a) {
    int sum = 0;
    int b = 0;
    for (int i = 0; i < n; i++) {
        if (b > 0) {
            b += a[i];
        } else {
            b = a[i];
        }
        if (b > sum) {
            sum = b;
        }
    }
    return sum;
}

凸多边形最优三角剖分

定义

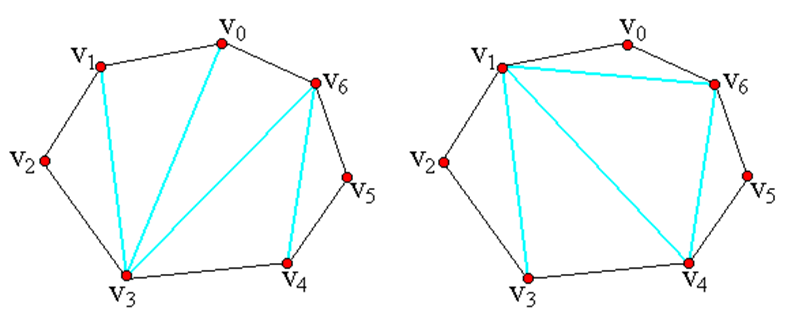
用多边形顶点的逆时针序列表示凸多边形
若vi与vj是多边形上不相邻的2个顶点，则线段vivj称为多边形的一条弦。
多边形的三角剖分是将多边形分割成互不相交的三角形的弦的集合T。
给定凸多边形P，以及定义在由多边形的边和弦组成的三角形上的权函数w。要求确定该凸多边形的三角剖分，使得即该三角剖分中诸三角形上权之和最小。

状态转移方程

• 定义t[ i ][ j ]¹为凸子多边形{vi-1,vi,…,vj}²的最优三角剖分所对应的权函数值，为方便起见，设退化的多边形{vi-1,vi}具有权值0。据此定义，要计算的凸(n+1)边形P的最优权值为t[1][n]。

• t[i][j]的值可以利用最优子结构性质递归地计算。当j-i≥1时，凸子多边形至少有3个顶点。由最优子结构性质，t[i][j]的值应为t[i][k]的值加上t[k+1][j]的值，再加上三角形vi-1vkvj的权值，其中i≤k≤j-1。由于在计算时还不知道k的确切位置，而k的所有可能位置只有j-i个，因此可以在这j-i个位置中选出使t[i][j]值达到最小的位置。由此，t[i][j]可递归地定义为：

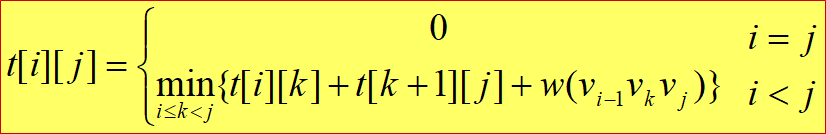
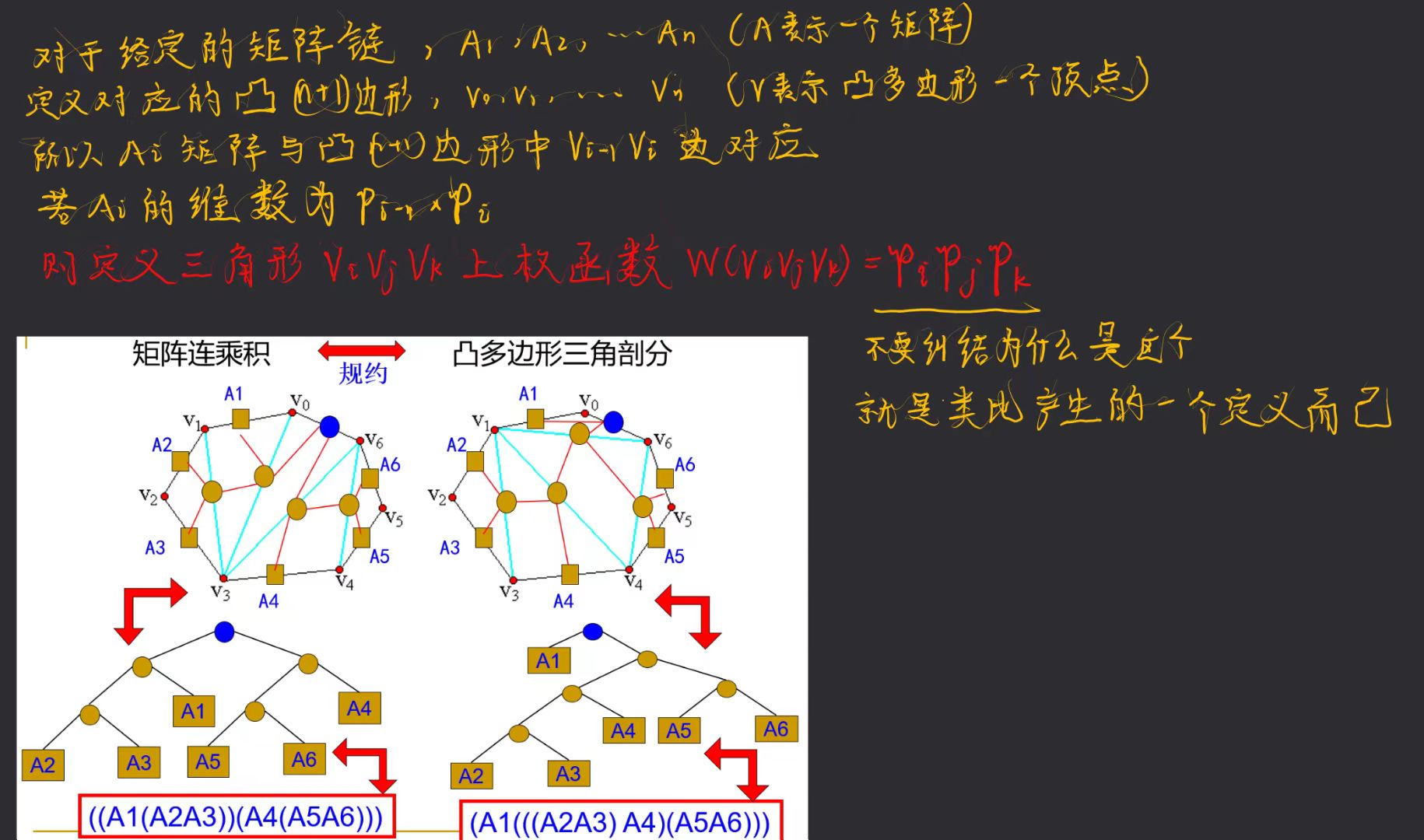
和之前矩阵连乘定义比较：

凸多边形是矩阵连乘的拓展，拓展结果就是最后w函数可以是各种自定义

代码

0-1 背包

定义：

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

0-1背包问题是一个特殊的整数规划问题。

动态转移方程

代码

原始版本求最大价值

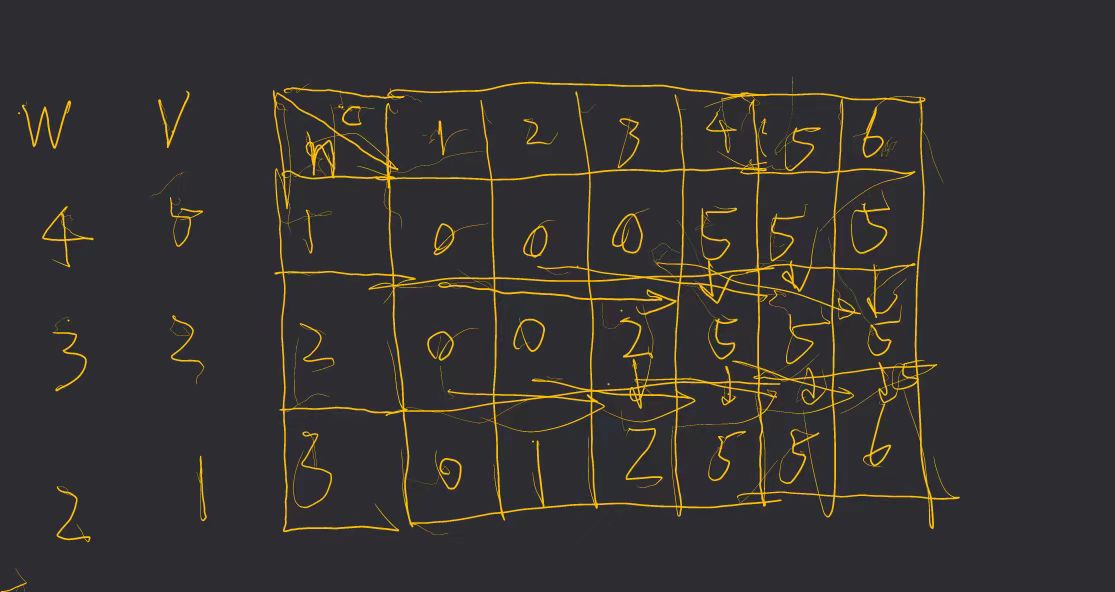
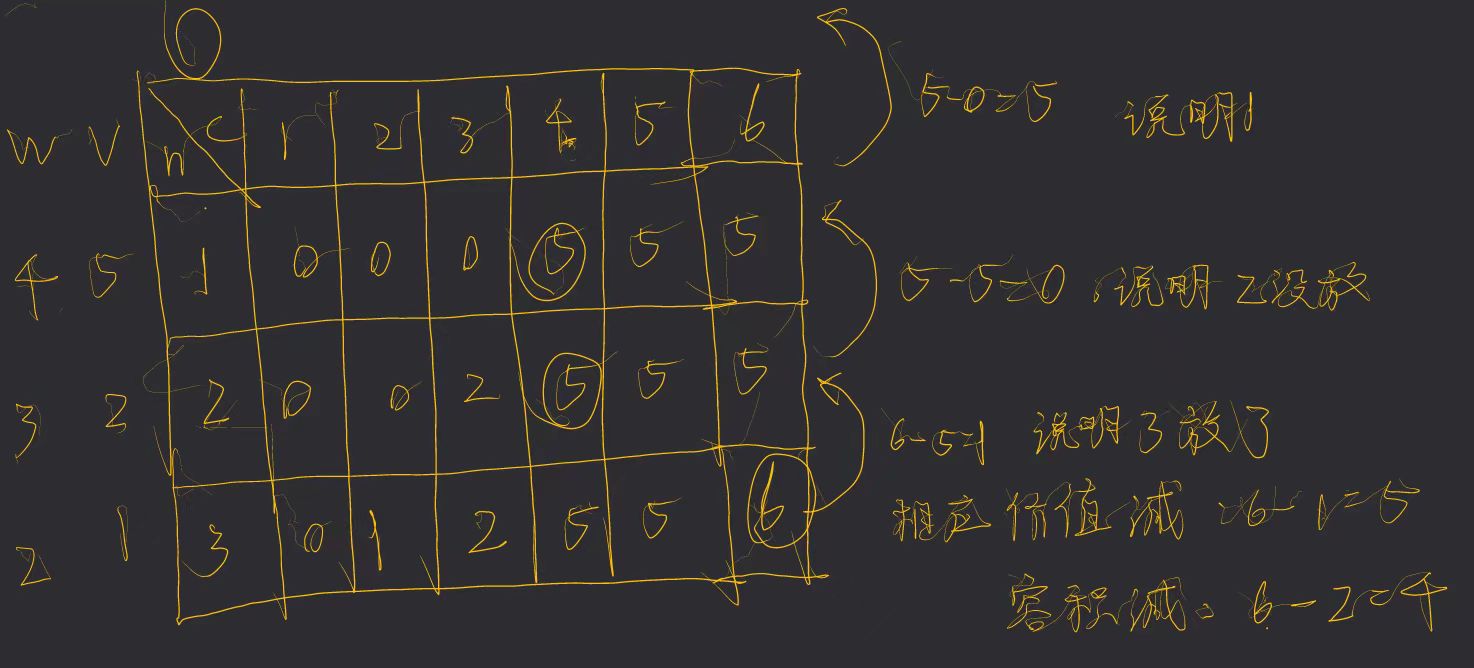
原始版本求产生最大价值的方法

流水作业调度

定义

n个作业{1，2，…，n}要在由2台机器M1和M2组成的流水线上完成加工。每个作业加工的顺序都是先在M1上加工，然后在M2上加工。M1和M2加工作业i所需的时间分别为ai和bi。流水作业调度问题要求确定这n个作业的最优加工顺序，使得从第一个作业在机器M1上开始加工，到最后一个作业在机器M2上加工完成所需的时间最少

直观来看，最佳调度应该是使机器M1没有空闲时间，同时机器M2的空闲时间最少。通常情况下，机器M2上会出现两种情况：一种是机器空闲，另一种是作业积压。

假设所有作业的集合为N={1, 2, ..., n}。S⊆N是N的作业子集。在一般情况下，当机器M1开始处理S中的作业时，机器M2可能正在处理其他作业，需要等待时间t才能开始处理S中的作业。我们将在这种情况下完成S中作业所需的最短时间记为T(S, t)。流水作业调度问题的最优解为T(N, 0)。(t = 0表示机器M2积压时间为0)

Johnson不等式

如果作业i和j满足min{bi,aj}≥min{bj,ai}，则称作业i和j满足Johnson不等式。

算法

流水作业调度问题的Johnson算法 (1)令

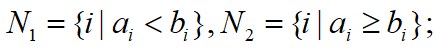(2)将N1中作业依ai的递增排序(不严格)；将N2中作业依bi的递减排序(不严格)； (3)N1中作业接N2中作业构成满足Johnson法则的最优调度。

视频讲解

最优二叉搜索树

二叉搜索树定义

若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
它的左、右子树也分别为二叉排序树。

如下图所示

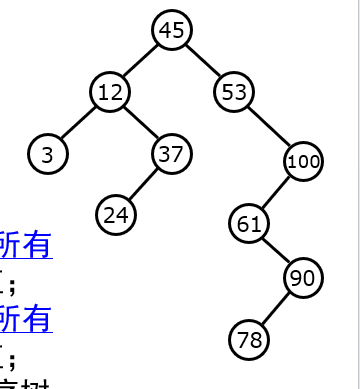
搜索的期望耗费

所有节点（包括成功与不成功）的概率和是1

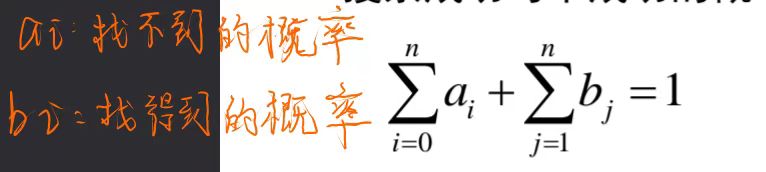
期望耗费

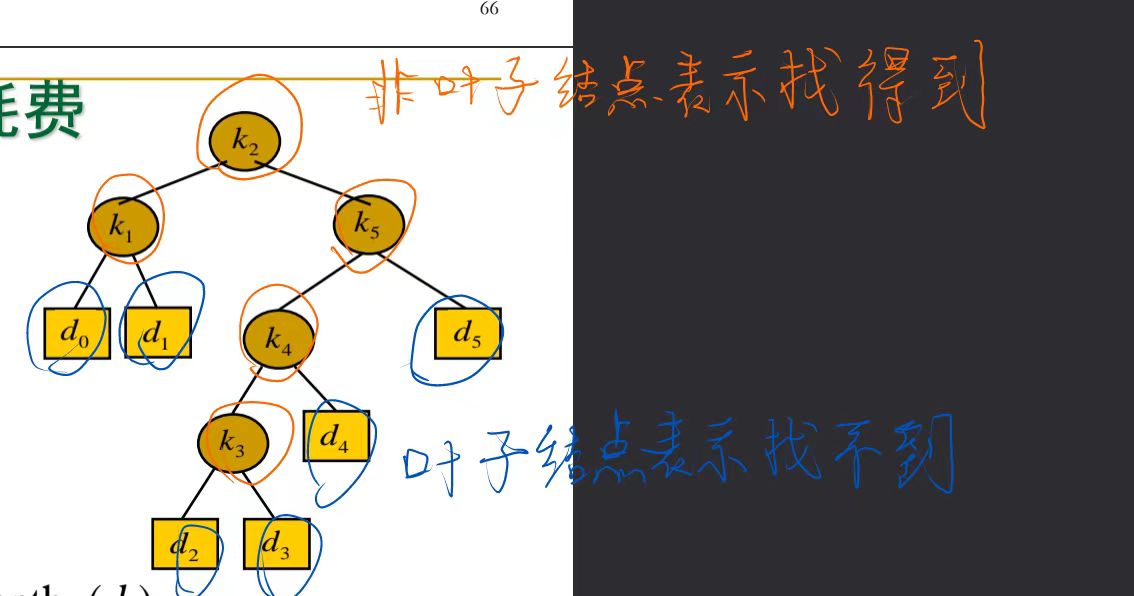
从深度角度（根节点深度为0）

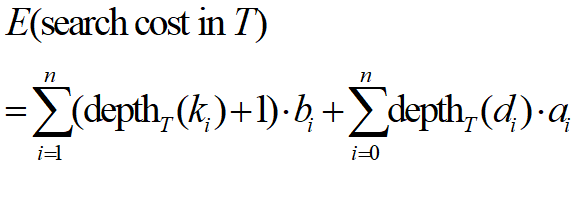
举例：

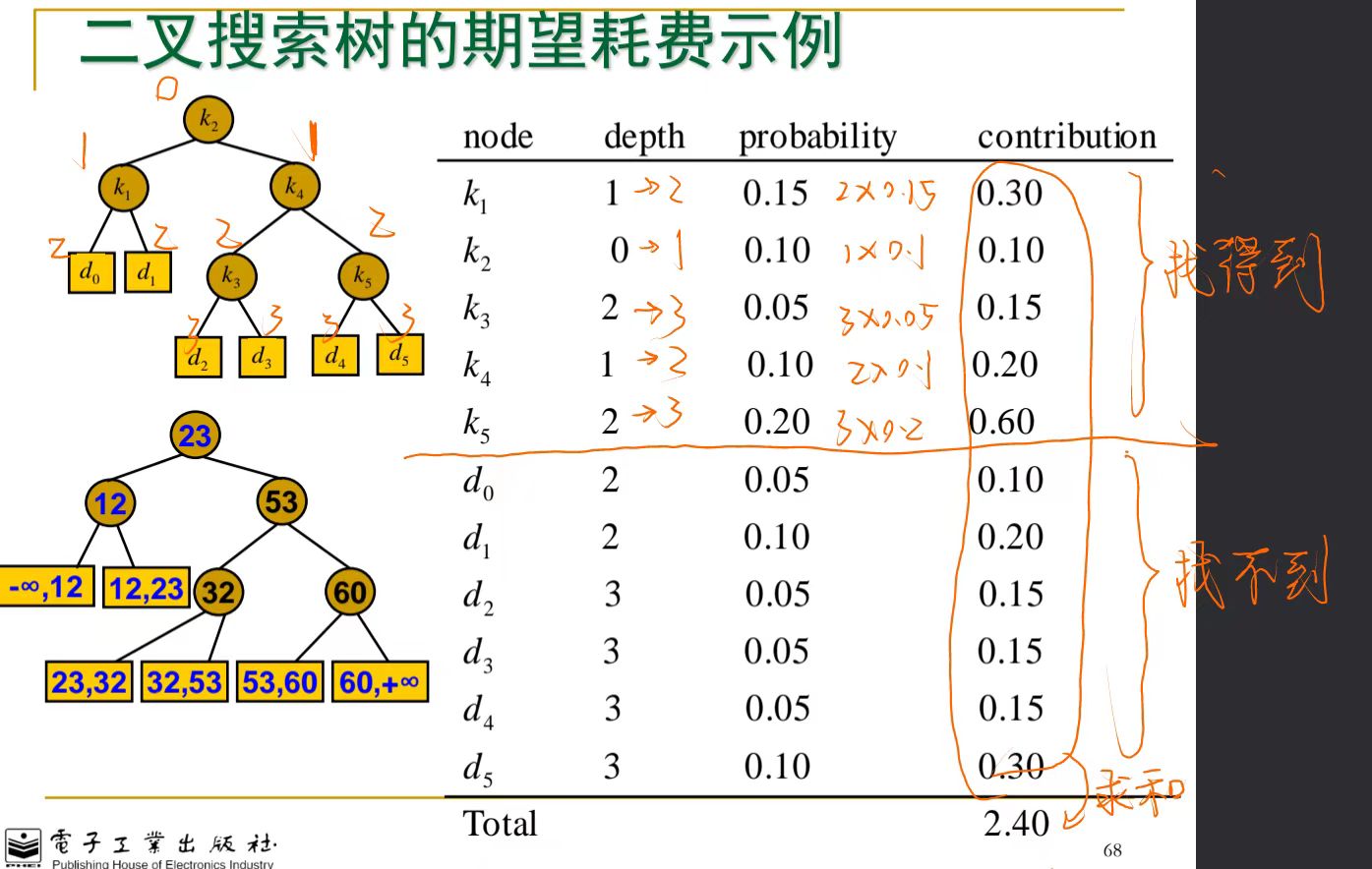
也可以从比较次数角度，比如根节点比较1次就能确定

构建最优二叉搜索树

任务描述

给了一堆节点和每个节点被搜索到的概率，要求建立一棵二叉搜索树，这棵树的期望耗费要最小

问题分析

最优子结构

\(w_{i, j}\)表示包括i到j的节点组成的子树的可能性的和，从i到j的节点是实际存在的节点序号，但是还包括他们的子节点

\(p_{i, j}\)表示包括i到j的节点组成的子树的平均“路长”

\(w_{i, j}p_{i,j}\)的积表示的是包括i到j的节点组成的树的"贡献"

一棵树要想期望耗费最小，就是这棵树的左右子树贡献最小

状态转移方程

代码分析

Void OBST (int* a, int* b, int n, int **m, int **s, int **w) 
{  for (int i=0;i<=n;i++) { w[i+1][i]=a[i]; m[i+1][i]=0; } //初始状态
   for (int r=0;r<n;r++)              //r+1为结点个数
      for (int i=0;i<=n-r;i++)   //考虑xi～xj共r+1个结点的
      { int j=i+r;                       //最优二叉搜索树
         w[i][j]=w[i][j-1]+a[j]+b[j];       //以xi为根节点
         m[i][j]=m[i+1][j]; s[i][j]=i;      //注意m(i,i-1)=0
         for (int k=i+1; k<=j; k++)
           { int t=m[i][k-1]+m[k+1][j];    //以xk为根节点
              if (t<m[i][j])      //t为当前最小值
                   { m[i][j]=t; s[i][j]=k; } //s记录当前子树根节点xk
           }
         m[i][j] += w[i][j];
       }
}

上面最好要有个矩阵模拟过程

问题：数组a是什么？数组b又是什么？